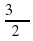Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Градусное и радианное измерение углов
Урок полностью соответствует программе. Учащиеся знакомятся с новой единицей измерения углов – радиан. Урок состоит из 5 этапов:
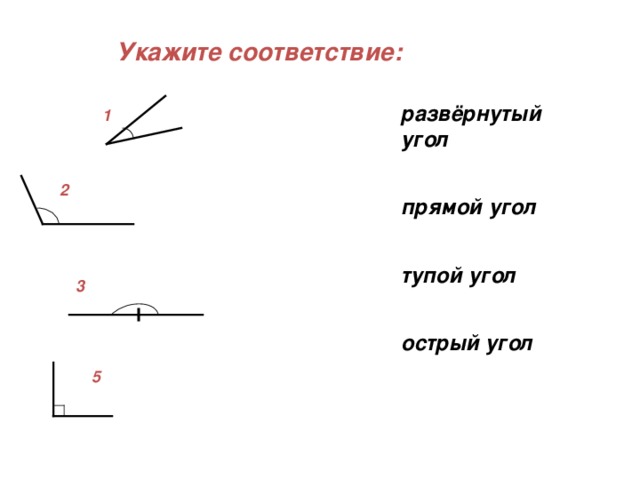
1. Повторение (повторение типы углов, ранее изученной единицы измерения градус)
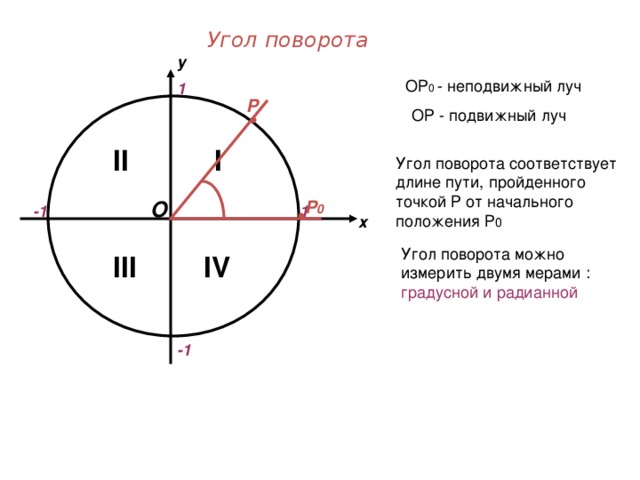
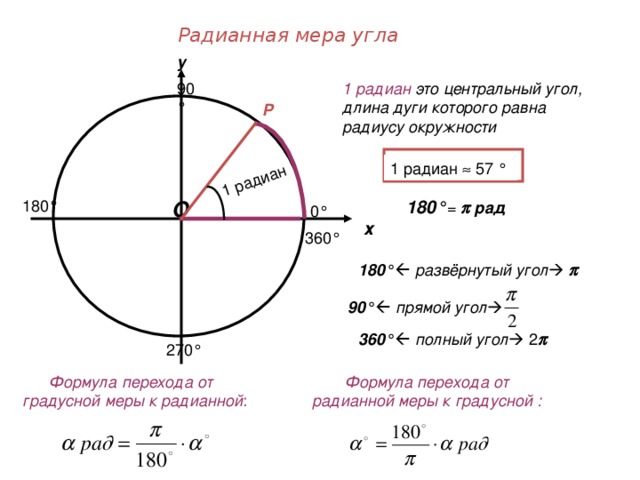
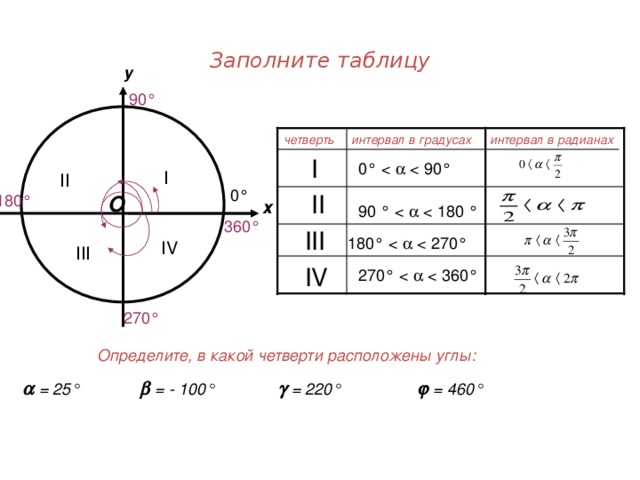
2.Новая тема (объяснение, вводится радианное измерение углов, рассказывается о делении единичной окружности по четвертям)
3. Закрепление (самостоятельное решение примеров, привить умения и навыки переводить градусы в радианы, определять в какой четверти расположен угол)
4. Выставление оценок (наиболее активно и правильно решившим все задания выставлятся оценки «отлично», сделавшим одну-две ошибки «хорошо», за три и более – «удовлетворительно»
6. Домашнее задание
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«градусная и радианная мера угла»
Просмотр содержимого презентации
«угол поворота»
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1720 руб.
2860 руб.
1720 руб.
2860 руб.
1720 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
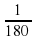 часть развёрнутого угла.
часть развёрнутого угла. 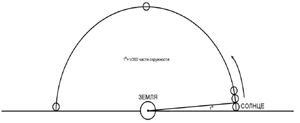
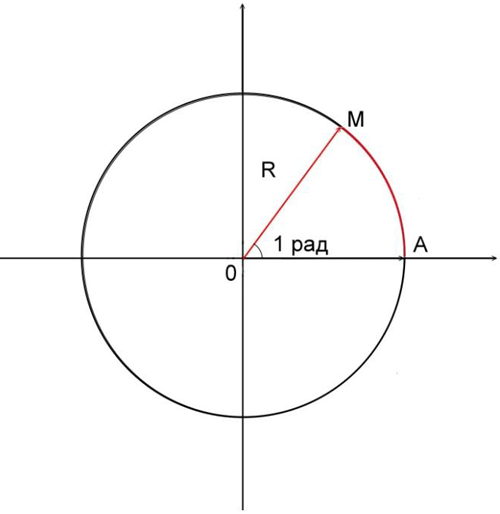
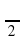
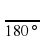 и 1 рад =
и 1 рад =  , откуда вытекают формулы перехода от радианной меры к градусной и от градусной меры к радианной.
, откуда вытекают формулы перехода от радианной меры к градусной и от градусной меры к радианной.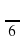 и
и 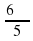 в градусную меру, а 45° и 540° в радианную.
в градусную меру, а 45° и 540° в радианную.