Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
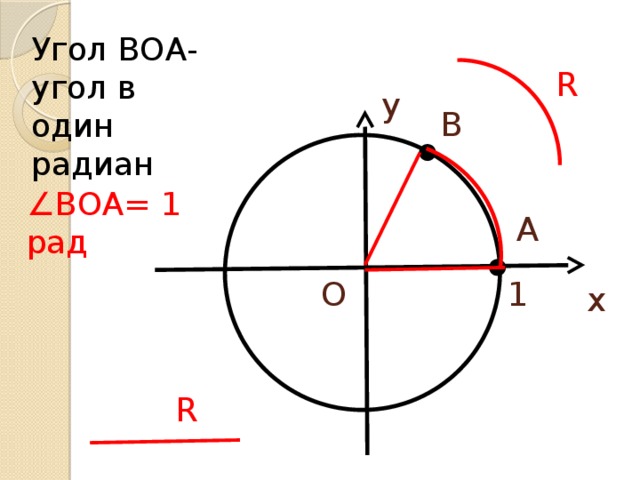
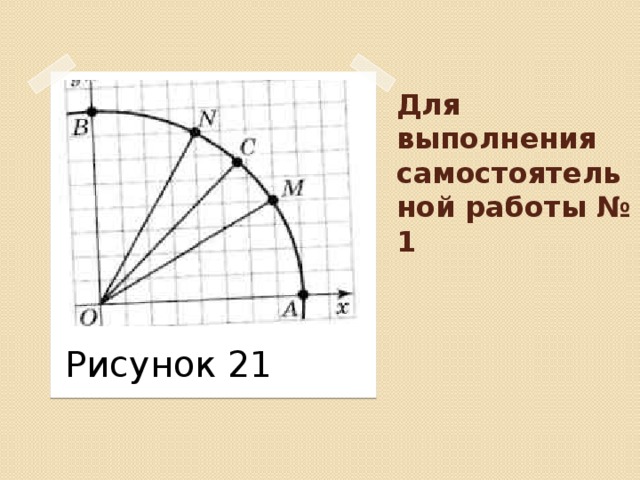
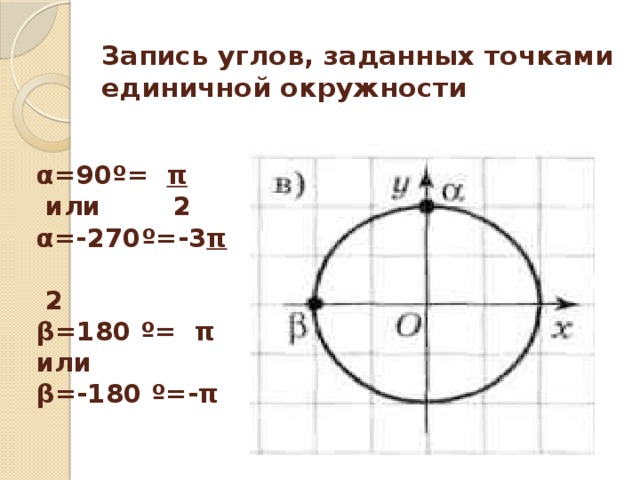
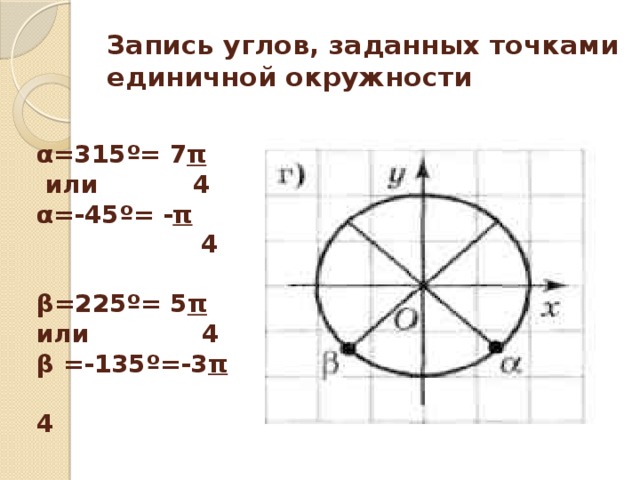
В данной презентации рассматривается определение радианной меры угла. История возникновения данной меры. Радианная мера угла является ведущей при работе на единичной окружности. поэтому появляется необходимость вывода формул перевода градусной и радианной мер. В материале приводятся ряд упражнений по оnработке навыков перевода радианной меры в градусную и наоборот.
Радианная мера угла
Угол ВОА- угол в один радиан
R
у
В
∠ ВОА= 1 рад
А
О
1
х
R
Длина окружности составляет С= 2 π R и R=1
Совершив один полный оборот против часовой стрелки (то есть угол в 360º) , получим угол в 2 π ·1 радиан≈2 ·3,14=6,28
360º - 2 π радиан
α º - α радиан
Значит угол в α радиан
α рад= 180º · α
π
Значит угол в 1 радиан
360º:2 π=180º⁄π ≈57º17’45’’
Значит угол в α градус
α º = π · α
180º
Значит угол в 1 градус
2 π:360º=π⁄ 180ºрадиан
Желаю успехов
Домашнее задание
Для выполнения самостоятельной работы № 1
Рисунок 21
Запись углов, заданных точками единичной окружности
α=90º= π
или 2
α=-270º=-3 π
2
β=180 º= π
или
β=-180 º=-π
Запись углов, заданных точками единичной окружности
α =315º= 7 π
или 4
α=-45º= - π
4
β=225º= 5 π
или 4
β =-135º=-3 π
4
Запись углов, заданных точками единичной окружности
α=30º+360º· п
= π +2π· п, где п є Z
6
β=210º +360º· п
= 7π + 2π · п, где п є Z
6
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
