Изучение экономических приложений математики позволит будущему специлисту сформировать компоненты своего мышления
- Меню
- Главная
- Дошкольное образование
- Начальные классы
- Астрономия
- Биология
- География
- Информатика
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- Русский язык
- Английский язык
- Немецкий язык
- Французский язык
- История
- Естествознание
- Всемирная история
- Всеобщая история
- История России
- Право
- Окружающий мир
- Обществознание
- Экология
- Искусство
- Литература
- Музыка
- Технология (мальчики)
- Технология (девочки)
- Труд (технология)
- Физкультура
- ИЗО
- МХК
- ОБЗР (ОБЖ)
- Внеурочная работа
- ОРК
- Директору
- Завучу
- Классному руководителю
- Экономика
- Финансовая грамотность
- Психологу
- ОРКиСЭ
- Школьному библиотекарю
- Логопедия
- Коррекционная школа
- Всем учителям
- Прочее
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
- Главная
- Математика
- Уроки
- Элементы линейного программирования
Элементы линейного программирования
Просмотр содержимого документа
«Элементы линейного программирования»
64
Департамент образования и науки Пермской области
«Элементы линейного программирования»
(факультативный курс для группы «коммерсант промышленности»)
Методическое пособие для преподавателя
Выполнила: Есенеева
Эльвира Самигулловна,
преподаватель математики
ГБОУ СПО
«ПАПТ»
- Пермь, 2011 -
Содержание
стр
Пояснительная записка_________________________________________________3
Тематический план____________________________________________________ 4
Введение____________________________________________________________ 5
Классификация моделей________________________________________________6
Основные этапы построения математических моделей______________________ 9
Постановка задачи линейного программирования_________________________ 10
Графический метод___________________________________________________12
Транспортная задача. Общая постановка задачи___________________________16
Открытые и закрытые транспортные задачи______________________________18
Построение начального плана транспортной задачи по правилу «северо-западного угла»______________________________________________________ 19
Метод минимального элемента_________________________________________ 21
Метод потенциалов___________________________________________________22
Вырожденность в транспортных задачах_________________________________ 28
Приложения транспортных моделей_____________________________________30
Решение транспортной задачи средствами MathCAD_______________________33
Задача о назначениях ________________________________________________ 36
Симплекс – метод____________________________________________________ 40
Приложение 1 (Контрольные задания по теме «Графический метод)________ 46
Приложение 2 (Контрольные задания по теме «Транспортные задачи)_______51
Приложение 3 (Контрольные задания по теме «Задачи о назначениях)_______57
Приложение 4 (Контрольные задания по теме «Симплекс – метод»)________ 61
Приложение 5 (Вопросы к зачету)______________________________________62
Литература _________________________________________________________63
Пояснительная записка
Современная математика характеризуется интенсивным проникновением в другие науки, во многом этот процесс происходит благодаря разделению математики на ряд самостоятельных областей. Язык математики оказался универсальным, то есть она пытается отразить, или промоделировать, на своем специфическом языке закономерности окружающего мира.
Изучение экономических приложений математики, составляющих основу актуальной экономической математики, позволит будущему специалисту не только приобрести необходимые базовые навыки, используемые в экономике, но и сформировать компоненты своего мышления: уровень, кругозор и культуру. Все это понадобится для успешной работы по окончании учебного заведения и для ориентации в будущей профессиональной деятельности.
Учитывая современные требования, необходимые для специалистов связанных с экономикой и воспитания конкурентоспособного выпускника возникла необходимость введение данного курса в группе «коммерсант промышленности».
Программа данного факультатива рассчитана на 30 часов и включает 4 раздела:
- Графический метод решения задач линейного программирования;
- Транспортная задача;
- Задача о назначениях;
- Решение задач линейного программирования симплекс – методом.
Темы выбраны с учетом требований математической подготовки учащихся в средней школе и их профессиональной деятельности.
После изучения каждой темы разбирается решение одной или нескольких задач. В конце каждого раздела выполняется контрольная работа (10 вариантов заданий) которая позволяет закрепить и проверить умения и навыки учащихся по пройденной теме.
Тематическое планирование
| № п/п | Содержание учебного материала (всего30 часов) | Кол – во часов |
| 1 | Введение. Классификация моделей. Основные этапы построения моделей. | 1 |
| 2 | Постановка задачи линейного программирования. | 1 |
| 3 | Графический метод. Решение задач. | 2 |
| 4 | Контрольная работа. | 1 |
| 5 | Общая постановка транспортной задачи. Открытые и закрытые транспортные задачи. Приведение открытой транспортной задачи к закрытой. | 2 |
| 6 | Построение начального плана транспортной задачи по правилу « северо–западного» угла. | 1 |
| 7 | Методы решения транспортных задач. Метод минимального элемента. | 1 |
| 8 | Проверка полученного решения на оптимальность. Метод потенциалов. | 2 |
| 9 | Вырожденность в транспортных задачах. | 2 |
| 10 | Приложения транспортных моделей. | 2 |
| 11 | Решение транспортных задач с помощью математического пакета MathCAD. | 2 |
| 12 | Контрольная работа . | 2 |
| 13 | Задача о назначениях. Общая постановка задачи. | 1 |
| 14 | Венгерский метод решения задачи о назначениях. Решение задач. | 1 |
| 15 | Контрольная работа. | 1 |
| 16 | Симплекс – метод. Алгоритм решения задач линейного программирования симплекс – методом. | 3 |
| 17 | Контрольная работа. | 2 |
| 18 | Обобщение. | 1 |
| 19 | Зачет. | 2 |
Введение
Экономические проблемы, возникающие перед специалистами в большинстве своем сложные. Они зависят от множества различных, иногда противоречащих друг другу факторов, изменяются с течением времени и влияют на другие проблемы и процессы.
Для принятия обоснованного решения необходимо иметь и обработать большое количество информации, определяемое иногда астрономическими цифрами. Принятие ответственных решений, как правило, связано с большими материальными ценностями. В настоящее время недостаточно знать путь, ведущий к достижению цели. Необходимо из всех возможных путей выбрать наиболее экономичный, который наилучшим образом соответствует поставленной задаче.
Появление цифровых вычислительных машин и персональных компьютеров создало огромные возможности для развития науки, совершенствования методов планирования и управления производством. Однако без строгих формулировок задач, без математического описания процессов современный уровень управления и планирования не может быть достигнут.
Впервые математические модели были использованы для решения практической задачи в 30-х годах в Великобритании при создании систем противовоздушной обороны. Для разработки данной системы были привлечены ученые различных специальностей. Система создавалась в условиях неопределенности относительно возможных действий противника, поэтому исследования проводились на адекватных математических моделях. В это время впервые был применен термин «операционное исследование», подразумевавший исследования военной операции. В последующие годы операционные исследования или исследования операций развиваются как наука, результаты которой применяются для выбора оптимальных решений при управлении реальными процессами и системами.
Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств. Собственно говоря, сама математика обязана своим существованием тому, что она пытается отразить, т.е. промоделировать, на своем специфическом языке закономерности окружающего мира.
Определение 1. Математическая модель-это система математических соотношений, приближенно, в абстрактной форме описывающих изучаемый процесс или систему.
Определение 2. Экономико-математическая модель-это математическая модель, предназначенная для исследования экономической проблемы.
В настоящее время математические модели применяются для анализа, прогнозирования и выбора оптимальных решений в различных областях экономики. Это планирование и оперативное управление производством, управление трудовыми ресурсами, управление запасами, распределение ресурсов, планировка и размещение объектов, руководство проектом, распределение инвестиций и т.п.
Классификация моделей
ММ можно классифицировать следующим образом: (см. схему)
По числу критериев эффективности ММ делятся на однокритериальные и многокритериальные. Многокритериальные содержат 2 или более критерия.
По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности.
В детерминированных моделях не учитываются неизвестные факторы. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи, в том числе большинство экономических. По виду целевой функции и ограничений детерминированные модели делятся на линейные, нелинейные, динамические и графические.
В линейных моделях целевая функция и ограничения линейны по управляющим переменным.
Построение и расчет линейных моделей являются наиболее развитым разделом ММ, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения.
Нелинейные модели – это модели, в которых либо целевая функция, либо какое–нибудь из ограничений (либо все ограничения нелинейные по управляющим переменным. (т. е. переменная не в первой степени). Для нелинейных моделей нет единого метода расчета и поэтому можно предложить различные способы решения. Однако может случиться так, что для поставленной нелинейной задачи вообще не существует метода расчета. В этом случае задачу следует упростить, сведя его к известным линейным моделям.
В динамических моделях в отличие от линейных и нелинейных моделей учитывается фактор времени. Критерий оптимальности в этих моделях может быть самого общего вида(и вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения.
Классификация моделей
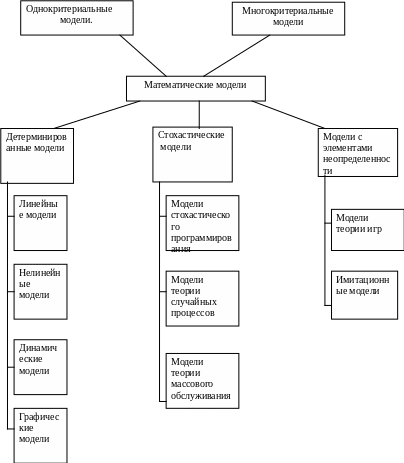
Графические модели используются тогда, когда задачу удобно представить в виде графической структуры.
В стохастических моделях неизвестные факторы - случайные величины, для которых известны функции распределения и различные статистические характеристики ( математическое ожидание, дисперсия, среднеквадратическое отклонение и т.п.). среди них можно выделить:
- модели стохастического программирования, в которых либо в целевую функцию, либо в ограничения входят случайные величины;
- модели теории случайных процессов, предназначенные для изучения процессов, состоятие которых в данный момент времени является случайной величиной;
- модели теории массового обслуживания, в которой изучаются многоканальные системы, занятые обслуживанием требований.
Модели с элементами неопределенности предназначены для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные и значения которых неопределены. В моделях теории игр задача представляется в виде игр, в которой участвуют несколько игроков, преследующих различные цели, например организация предприятия в условиях конкуренции.
В имитационных моделях реальный процесс разворачивается в машинном времени, и прослеживаются результаты случайных воздействий на него, например организация производственного процесса.
Основные этапы построения математических моделей
Определение цели, т.е чего хотят добиться решая поставленную задачу.
Определение параметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет.
Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных и являются решениями задачи.
Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.
Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным и неопределенным образом.
Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.е. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи.
Постановка задачи линейного программирования
Определение1: Линейное программирование – наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.
Линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений и неравенств, называются системой ограничений.
Определение 2: Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи.
В общем виде математическая модель задачи линейного программирования (ЛП) записывается так:
![]()
при ограничениях:
![]()
![]() .
.
Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.
Математическая модель в более краткой записи имеет вид:
![]()
при ограничениях:
![]() .
.
Определение 3: Допустимым решением (планом) задачи линейного программирования называется вектор ![]() .
.
Множество допустимых решений образует область допустимых решений (ОДР).
Определение 4: Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением задачи линейного программирования и обозначается ![]() .
.
I раздел
Графический метод
Графический метод является наиболее простым и наглядным методом линейного программирования.
Применяется для решения задач линейного программирования с 2-мя переменными.
С геометрической точки зрения в задаче ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя или нижняя линия уровня или точка выхода линии уровня из области допустимых решений.
Для нахождения экстремального значения целевой функции при графическом методе используют вектор, показывающий направление наискорейшего изменения целевой функции С.
Алгоритм решения задач ГМ.
1. Находим область допустимых решений системы ограничений задачи.
Строим вектор С.
Проводим линию уровня L0, которая перпендикулярна С.
Линию уровня перемещаем по направлению вектора С для задач на максимум и в направлении противоположном С, для задач на минимум.
Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение задачи, и будет точкой экстремума. Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача будет иметь бесчисленное множество решений.
5.Находим координаты точки экстремума и значение целевой функции в ней.
В
озможны следующие случаи ОДР:
Пример. Выбор оптимального выпуска изделий.
Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются 2 вида продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы заданы в таблице.
| Исходный продукт | Расход исходных продуктов | Запас,кг | |
|
| сливочное | шоколадное |
|
| Молоко | 0,8 | 0,5 | 400 |
| Наполнители | 0,4 | 0,8 | 365 |
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 руб., шоколадного – 14 руб.
Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?
Решение.
Обозначим: х1 – суточный объем выпуска сливочного мороженого, кг; х2 - суточный объем выпуска шоколадного мороженого, кг.
Составим математическую модель задачи.
Целевая функция будет иметь вид:
L(x) = 16x1+14x2 – max при ограничениях:
0,8 x1+ 0,5x2 400,
0,4x1+0,8x2 365,
x1-x2100,
x2350,
x10, x20.
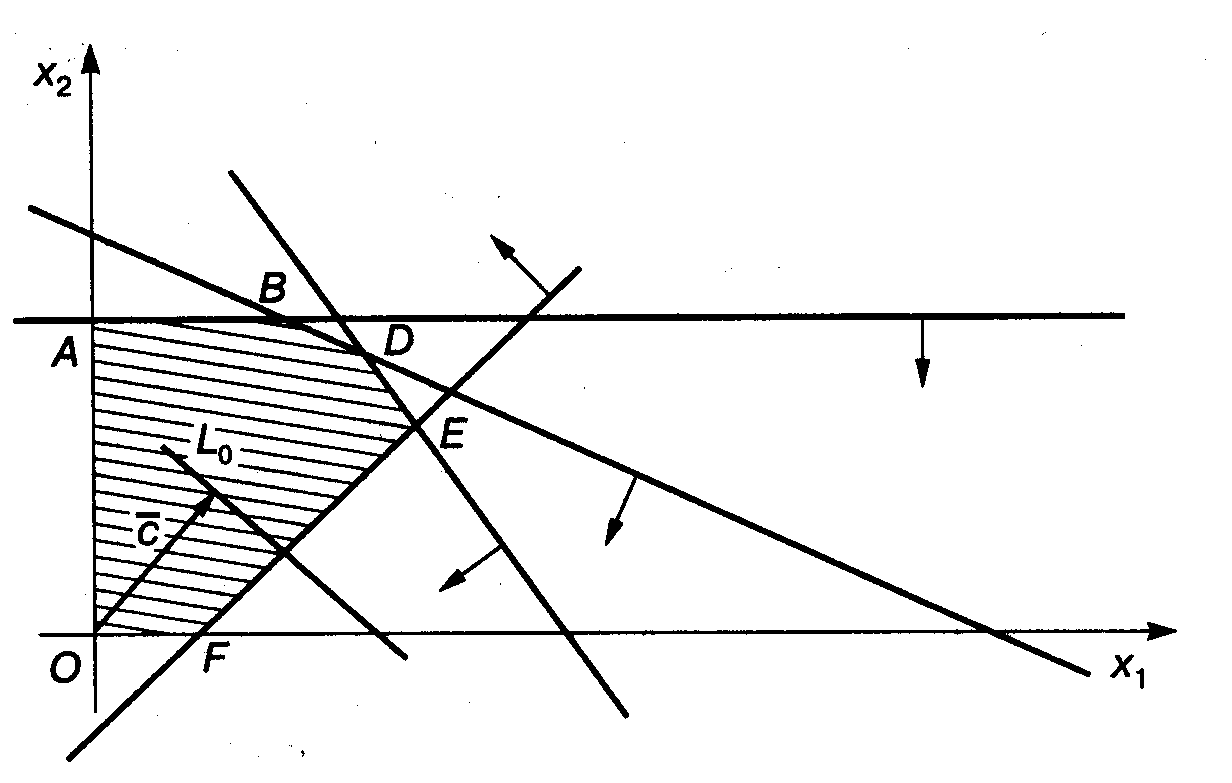
OABDEF – область допустимых решений. Строим вектор с(1;1). Линия уровня задается уравнением L0 = 16x1+14x2=const.
Перемещаем линию уровня по направлению вектора с. Точкой выхода L0 из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных уравнениями:
0,8х1+0,5х2=400
0,4х1+0,8х2 = 365.
Решая систему, получим координаты точки D ( 312,5; 300), в которой и будет оптимальное решение, т.е Хопт =(312,5; 300), при этом
L(x)max = 16*312,5 + 14*300 = 9200.
Таким образом, фирма должна выпускать в сутки 312,5 кг сливочного мороженого и 300 кг шоколадного мороженого, при этом доход от реализации составит 9200 рублей.
II раздел
Транспортная задача
Общая постановка задачи
Транспортная задача – одна из распространенных задач линейного программирования. Ее цель – разработка наиболее рациональных путей и способов транспонирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время продвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д.
В общем виде транспортную задачу можно представить следующим образом: Некий продукт (например, сталь) вырабатывается на m заводах ![]() , причем ежемесячная выработка составляет
, причем ежемесячная выработка составляет ![]() соответственно. Пусть эту сталь нужно доставить на предприятия
соответственно. Пусть эту сталь нужно доставить на предприятия ![]() (всего k), причем
(всего k), причем ![]() - ежемесячная потребность этих предприятий. Наконец, пусть задана стоимость
- ежемесячная потребность этих предприятий. Наконец, пусть задана стоимость ![]() , перевозки одной тонны стали с завода
, перевозки одной тонны стали с завода ![]() на предприятие
на предприятие ![]() . Принято считать, что общее производство стали равно суммарной потребности в ней:
. Принято считать, что общее производство стали равно суммарной потребности в ней:
а1+а2+…+ат= b1+b2+…bk.
Требуется составить план перевозок, при котором:
1) была бы точно удовлетворена потребность в стали предприятий ![]() ;
;
2) была бы вывезена вся сталь с заводов ![]() ;
;
3)общая стоимость перевозок была бы наименьшей.
Обозначим через ![]() количество стали (в тоннах), предназначенной к отправке с завода
количество стали (в тоннах), предназначенной к отправке с завода ![]() на предприятие
на предприятие ![]() . План перевозок состоит из
. План перевозок состоит из ![]() неотрицательных чисел
неотрицательных чисел ![]()
![]() .
.
|
| в | в | в | … | в | Отправлено |
| из |
|
|
| … |
|
|
| из |
|
|
| … |
|
|
|
|
|
|
| … |
|
|
| из |
|
|
| … |
|
|
| Привезено |
|
|
| … |
|
|
Условие 1) примет вид:
![]()
Условие 2) примет вид:
![]()
Раз стоимость перевозки одной тонны из Pi в Qj равна cij, то общая стоимость S всех перевозок равна S = c11x11+c12x12+…+c1kx1k+…+cmkxmk.
Таким образом, мы приходим к следующей чисто математической задаче: дана система m+k линейных уравнений с mk неизвестными и линейная функция S. Требуется среди всех неотрицательных решений данной системы найти такое, при котором функция S достигает наименьшего значения (минимизируется).
Открытые и закрытые транспортные задачи
В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми.
Определение 1: Если в транспортной задаче суммарный спрос потребителей и суммарное предложение поставщиков равны, то задача называется закрытой, т.е![]() . В противном случае задача называется открытой, т.е.
. В противном случае задача называется открытой, т.е. ![]() .
.
Приведение открытой транспортной задачи к закрытой
При открытой транспортной задаче сумма запасов не совпадает с суммой потребностей.
При этом :
1) если ![]() то объем запасов превышает объем потребления, все потребители будут удовлетворены полностью и часть запасов останется невывезенной. Для решения такой задачи вводят фиктивного (n+1)-го потребителя, потребности которого
то объем запасов превышает объем потребления, все потребители будут удовлетворены полностью и часть запасов останется невывезенной. Для решения такой задачи вводят фиктивного (n+1)-го потребителя, потребности которого ![]() .
.
2) Если ![]() то объем потребления превышает объем запасов, часть потребностей останется неудовлетворенной. Для решения задачи вводим фиктивного (m+1) –го поставщика:
то объем потребления превышает объем запасов, часть потребностей останется неудовлетворенной. Для решения задачи вводим фиктивного (m+1) –го поставщика: ![]() .
.
При введении фиктивного поставщика или потребителя открытая транспортная задача становится закрытой и решается по ранее рассмотренному алгоритму для закрытых транспортных задач. Тарифы, соответствующие фиктивному поставщику или потребителю, больше или равны наибольшему из всех транспортных тарифов, иногда их считают равными нулю. В целевой функции фиктивный поставщик или потребитель не учитываются.
Построение начального плана транспортной задачи по правилу
« северо–западного» угла.
Алгоритм.
1.Составляем транспортную таблицу;
2.Транспортную таблицу начинают заполнять с левого - верхнего (северо-западного) угла.
2.1. При заполнении двигаемся по строке вправо и по столбцу вниз. В клетку, находящуюся на пересечении первой строки и первого столбца, помещается максимально возможное число единиц продукции, разрешенное ограничениями на спрос и предложение.
2.2 . Если спрос удовлетворен – двигаемся по строке вправо, если исчерпано предложение – по столбцу вниз.
Процесс продолжается до тех пор, пока не исчерпается предложение и не удовлетворится спрос.
Пример.
На 3 складах имеются запасы продукции в количествах 110, 140, 190 тонн соответственно. 4 потребителя должны получить эту продукцию в количествах 90,150,160, 40 тонн соответственно. Расходы по перевозке 1 т продукции заданы матрицей:
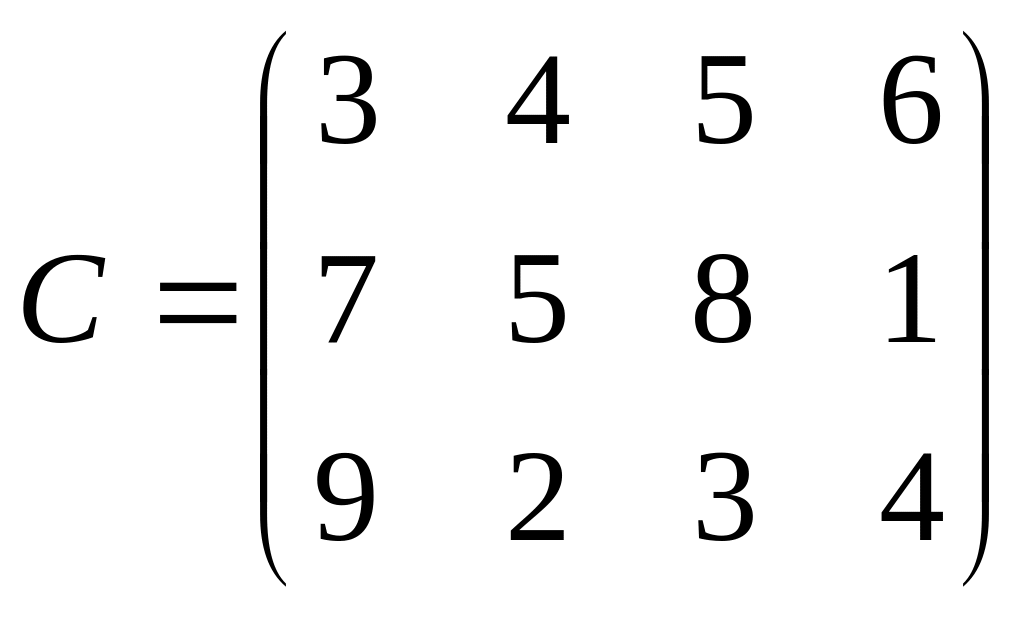
Определить начальное решение транспортной задачи, используя правило «северо-западного угла».
1) Заполним транспортную таблицу.
| № | 1 | 2 | 3 | 4 | Предложение |
| 1 | 90 3 | 20 4 | 5 | 6 | 110 |
| 2 | 7 | 130 5 | 10 8 | 1 | 140 |
| 3 | 9 | 2 | 150 3 | 40 4 | 190 |
| Спрос | 90 | 150 | 160 | 40 |
|
Решение:
1) В первую клетку помещаем ![]() . Спрос первого потребителя полностью удовлетворен, первый столбец вычеркивают.
. Спрос первого потребителя полностью удовлетворен, первый столбец вычеркивают.
2) Остаток сырья в первом пункте составляет : 110-90=20 у.е. Двигаемся по первой строке вправо ![]() . Предложение поставщика исчерпано, первая строка вычеркивается.
. Предложение поставщика исчерпано, первая строка вычеркивается.
3) Второму потребителю не хватает 150-20=130 у.е. Двигаемся по второму столбцу вниз ![]() . Второй столбец вычеркивается.
. Второй столбец вычеркивается.
4) Двигаемся по второй строке вправо ![]() . Вторая строка вычеркивается.
. Вторая строка вычеркивается.
5) Двигаемся по третьему столбцу вниз ![]() . Спрос третьего потребителя удовлетворен. Двигаемся по третьей строке вправо
. Спрос третьего потребителя удовлетворен. Двигаемся по третьей строке вправо ![]() . Спрос третьего потребителя удовлетворен.
. Спрос третьего потребителя удовлетворен.
6) Двигаемся по третьей строке вправо![]() .
.
Таблица заполнена. Начальный план перевозок имеет вид:
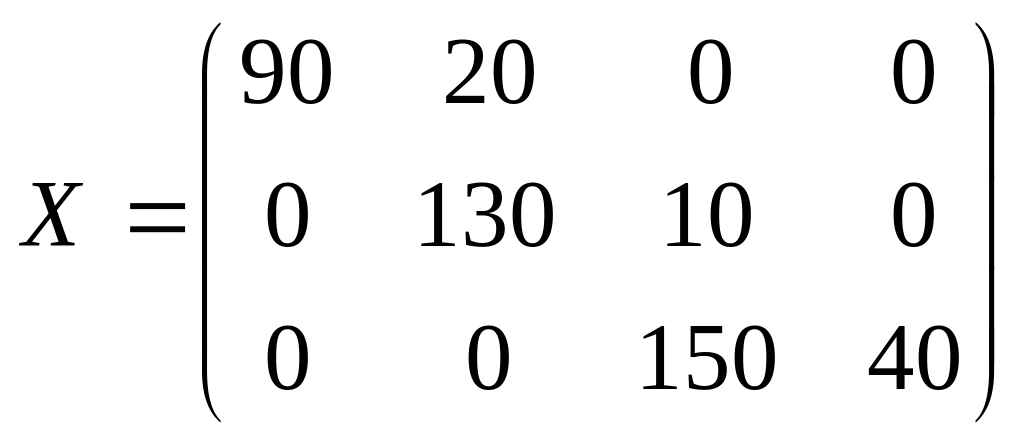
Стоимость перевозок по этому плану составляет
![]()
Использование данного правила - наиболее простой способ нахождения начального решения транспортной задачи. План перевозок, полученный этим способом обычно бывает далек от оптимального. Это происходит потому, что при его построении никак не учитываются значения тарифов сij. В связи с этим на практике для получения исходного плана используется другой способ – метод «минимального элемента», в котором при распределении объемов перевозок в первую очередь заполняются клетки с наименьшими тарифами.
Построение начального решения транспортной задачи
методом «минимального элемента»
Алгоритм.
1. Составляют транспортную таблицу.
2. Выбирают клетку таблицы, которой соответствует минимальное значение тарифа. Если клеток с одним и тем же минимальным тарифом несколько - выбирают любое из них.
3. В выбранную клетку аналогично правилу «северо-западного» угла помещают максимально возможное количество единиц продукции, разрешенное ограничениями на спрос и предложение. После этого, если предложение производителя исчерпано, вычеркивают соответствующую строку; если удовлетворен спрос - соответствующий столбец.
4. Если все клетки заполнены или вычеркнуты, то план перевозок построен. В противном случае, переходят к шагу 2 без учета заполненных и вычеркнутых клеток.
Пример.
Найдем начальное решение предыдущего примера методом «минимального элемента».
| № | 1 | 2 | 3 | 4 | Предложение |
| 1 | 90 3 | 4 | 20 5 | 6 | 110 |
| 2 | 7 | 5 | 100 8 | 40 1 | 140 |
| 3 | 9 | 150 2 | 40 3 | 4 | 190 |
| Спрос | 90 | 150 | 160 | 40 |
|
Минимальный тариф ![]() Спрос 4-го потребителя удовлетворен – соответственно 4-ый столбец вычеркиваем.
Спрос 4-го потребителя удовлетворен – соответственно 4-ый столбец вычеркиваем.
Минимальный тариф для оставшихся клеток ![]() Спрос 2-го потребителя удовлетворен – 2-ой столбец вычеркиваем.
Спрос 2-го потребителя удовлетворен – 2-ой столбец вычеркиваем.
Для оставшихся клеток минимальный тариф:
![]() Спрос 1-го потребителя удовлетворен - вычеркиваем 1-ый столбец.
Спрос 1-го потребителя удовлетворен - вычеркиваем 1-ый столбец.
Для оставшихся клеток минимальный тариф:
![]() Предложение 3-его поставщика исчерпано – вычеркиваем 3-ю строку.
Предложение 3-его поставщика исчерпано – вычеркиваем 3-ю строку.
Следующий минимальный тариф для оставшихся клеток: ![]() ,
,![]() Предложение 1-го поставщика исчерпано – вычеркиваем 1-ую строку.
Предложение 1-го поставщика исчерпано – вычеркиваем 1-ую строку.
Для последней оставшейся клетки:
![]() .
.
План перевозок, полученный по методу минимального элемента, имеет вид:
![]()
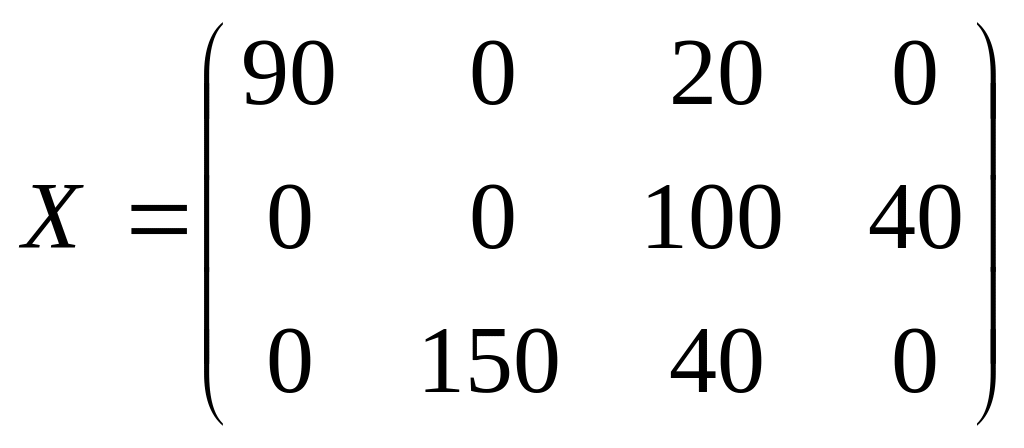
Стоимость перевозок по этому плану составляет
![]() у.е.
у.е.
Видим, что стоимость перевозок, полученных по методу минимального элемента, меньше стоимости перевозок, полученных с использованием правила «северо – западного угла» на 60 у.е. План, полученный данным методом более близок к оптимальному.
Проверка найденного решения на оптимальность
Метод потенциалов
Определение 1: Если при решении транспортной задачи число заполненных клеток транспортной таблицы равно m + n – 1, где m – где число производителей, а n – число потребителей, то план перевозок невырожденный.
Определение 2: Если число заполненных клеток транспортной таблицы меньше m + n – 1, где m – где число производителей, а n – число потребителей, то план перевозок вырожденный.
Вырожденный план перевозок получится, если на каком – то шаге одновременно удовлетворяется спрос потребителя и исчерпывается предложение поставщика, т.е. одновременно вычеркивается строка и столбец.
Для нахождения оптимального плана перевозок необходимо уметь оценивать полученный план на оптимальность.
Для оценки водится понятие косвенных затрат. Косвенные затраты – это затраты, получаемые для маршрутов, по которым не осуществляются перевозки при данном плане. Рассчитанные косвенные затраты сравниваются с реальными затратами, которые имели бы место, если бы перевозки по данным маршрутам осуществлялись. Если для всех невыбранных маршрутов косвенные затраты не больше реальных, то данный план перевозок является оптимальным. Если хотя бы для одного маршрута косвенные затраты больше реальных, то план перевозок может быть улучшен путем введения в него данного маршрута.
Рассмотрим получение оптимального плана перевозок с использованием метода потенциалов.
1 шаг: Получение начального плана перевозок .( методом «минимального элемента» или другим методом).
2 шаг: Проверка плана на невырожденность
Если полученный план вырожденный, то формально заполняют нулями некоторые из свободных клеток так, чтобы общее число занятых клеток было равно m + n – 1. Нули надо расставлять так, чтобы не образовался замкнутый цикл из занятых клеток.
3 шаг: Проверка плана на оптимальность
3.1 Определение потенциалов производителей и потребителей. Составляют систему уравнений для заполненных клеток транспортной таблицы: Ui +VJ = Cij,
где i , j – номера строк и столбцов, на пересечении которых стоят заполненные клетки, Ui потенциал i – го поставщика Vj – потенциал j –го потребителя Cij - тариф на перевозку из пункта i в пункт j. Для решения данной системы одно из неизвестных выбирают произвольно. Обычно полагают Ui = 0. Решая систему уравнений, находят значения потенциалов Ui и Vj , i =1,m, j = 1,n.
3.2. Определение суммы потенциалов (косвенных тарифов) для свободных клеток: C1qp = Uq + Vp , где q p – номера строк и столбцов, на пересечении которых стоит свободная клетка, Uq - потенциал q-го поставщика, Vp- потенциал p-го потребителя, C1qp – косвенные тарифы.
3.3 Проверка на оптимальность.
Для каждой свободной клетки таблицы составляется разность между C1qp и Cqp (косвенным и реальным тарифами) ![]() . Если все
. Если все ![]() , то полученный план оптимален. Если хотя бы для одной свободной клетки
, то полученный план оптимален. Если хотя бы для одной свободной клетки ![]() , то план может быть улучшен.
, то план может быть улучшен.
4 шаг. Улучшение плана
4.1 Выбирают клетку, которой соответствует максимальное положительное значение разности, полученной на шаге 3.3. Если имеется несколько одинаковых из них выбирают любое.
Переменная транспортной задачи, соответствующая этой клетке, вводится в список базисных переменных, т.е. данная клетка транспортной таблицы заполняется.
4.2 Выбор переменной выводимой из списка базисных переменных.
Заполнение клетки, выбранной на шаге 4.1, происходит следующим образом. Строят цикл, начинающийся и оканчивающийся в выбранной свободной клетке, содержащий в качестве вершин заполненные клетки таблицы и состоящий из горизонтальных и вертикальных отрезков. При этом в каждой клетке таблицы, являющейся вершиной цикла, соединяют обязательно горизонтальный и вертикальный отрезки. В свободной клетке условно ставят знак «+», а в остальных вершинах цикла, чередуясь ставят «-» и « + ».Затем происходит перераспределение продукции по циклу. Для этого выбирают клетку со знаком « - », которой соответствует наименьшее число единиц продукции. Это значение прибавляют к значениям, стоящим в клетках со знаком «+» и отнимают от значений, стоящих со знаком «-». При таком распределении общий баланс не изменяется. Свободная клетка заполняется. А клетка со знаком «-», которой соответствует наименьшее количество продукции, становится свободной.
Для нового плана повторяют все действия. (т.е переходят к шагу 2).
Пример 1.
Найти оптимальный план перевозок для транспортной задачи.
1) Получим начальный план решения методом минимального элемента.
| № | 1 | 2 | 3 | 4 | Предложение |
| 1 | 7 | 8 | 160 – 1 | + 2 | 160 |
| 2 | 120 4 | 5 | 9 | 20 8 | 140 |
| 3 | 9 | 50 2 | 30 + 3 | 90 – 6 | 170 |
| Спрос | 120 | 50 | 190 | 110 |
|

2) Проверим число заполненных клеток m+n-1= 4+3-1=6, т.е. данный план невырожденный. Определим потенциалы производителей и потребителей, составив уравнения Ui +VJ = Cij, для заполненных клеток и занесем их в таблицу:
2.1 U1+V3=1, U1=0, V1=0,
U2+V1=4, U2=4, V2=0,
U2+V4=8, U3=2. V3=1,
U3+V2=2, V4=4.
U3+V3=3,
U3+V4=6.
2.2 Составим разности для свободных клеток :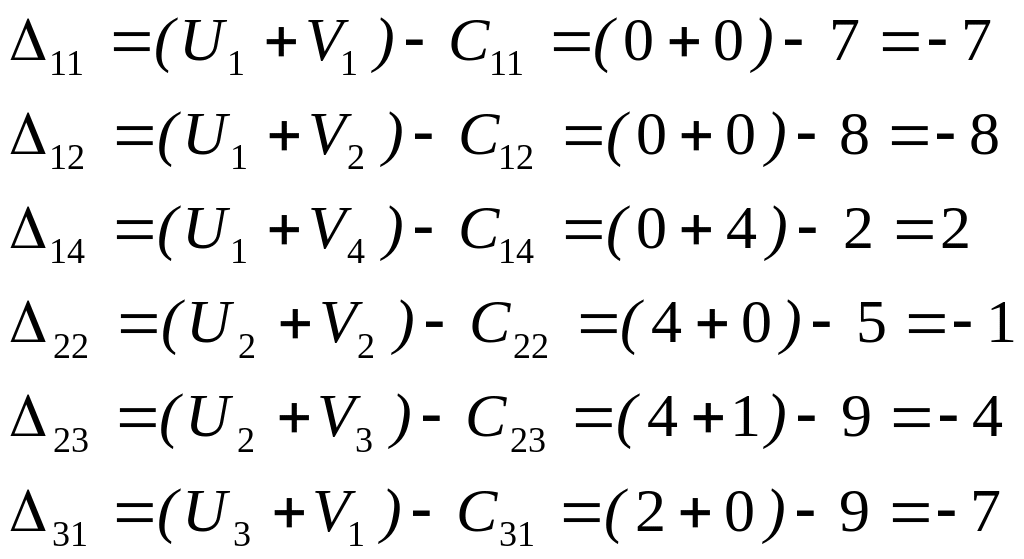
![]()
Получена положительная разность ![]() . Заполним клетку первой строки и четвертого столбца. Строим цикл, начинающийся и заканчивающийся в этой клетке. Вершинами цикла являются клетки: (3,4), (3,3), (1,3). В клетке (1,4) ставим «+», в клетке (3,4) – «-», в клетке (3,3) «+», в клетке (1,3) ставим « - ». Перераспределяем продукцию по циклу. Минимальное значение для клеток со знаком « - » находится в клетке (3,4) х34=90. Отнимаем 90 от значений, стоящих в клетках со знаком « - », и прибавляем к значениям, стоящим в клетках со знаком «+». Получаем новый план перевозок, представленный в следующей транспортной таблице:
. Заполним клетку первой строки и четвертого столбца. Строим цикл, начинающийся и заканчивающийся в этой клетке. Вершинами цикла являются клетки: (3,4), (3,3), (1,3). В клетке (1,4) ставим «+», в клетке (3,4) – «-», в клетке (3,3) «+», в клетке (1,3) ставим « - ». Перераспределяем продукцию по циклу. Минимальное значение для клеток со знаком « - » находится в клетке (3,4) х34=90. Отнимаем 90 от значений, стоящих в клетках со знаком « - », и прибавляем к значениям, стоящим в клетках со знаком «+». Получаем новый план перевозок, представленный в следующей транспортной таблице:
| № | 1 | 2 | 3 | 4 | Предложение |
| 1 | 7 | 8 | 70 – 1 | 90 + 2 | 160 |
| 2 | 120 4 | + 5 | 9 | 20 – 8 | 140 |
| 3 | 9 | 50 – 2 | 120 + 3 | 6 | 170 |
| Спрос | 120 | 50 | 190 | 110 |
|
3 ) Проверим число заполненных клеток: m+n-1=4+3-1= 6 - план невырожденный.
) Проверим число заполненных клеток: m+n-1=4+3-1= 6 - план невырожденный.
4) Проверим на оптимальность.
4.1 U1+V3=1, U1=0, V1=-2,
U1+V4=2, U2=6, V2=0,
U2+V1=4, U3=2. V3=1,
U2+V4=8, V4=2.
U3+V2=2,
U3+V3=3.
4.2 Составим разности для свободных клеток:
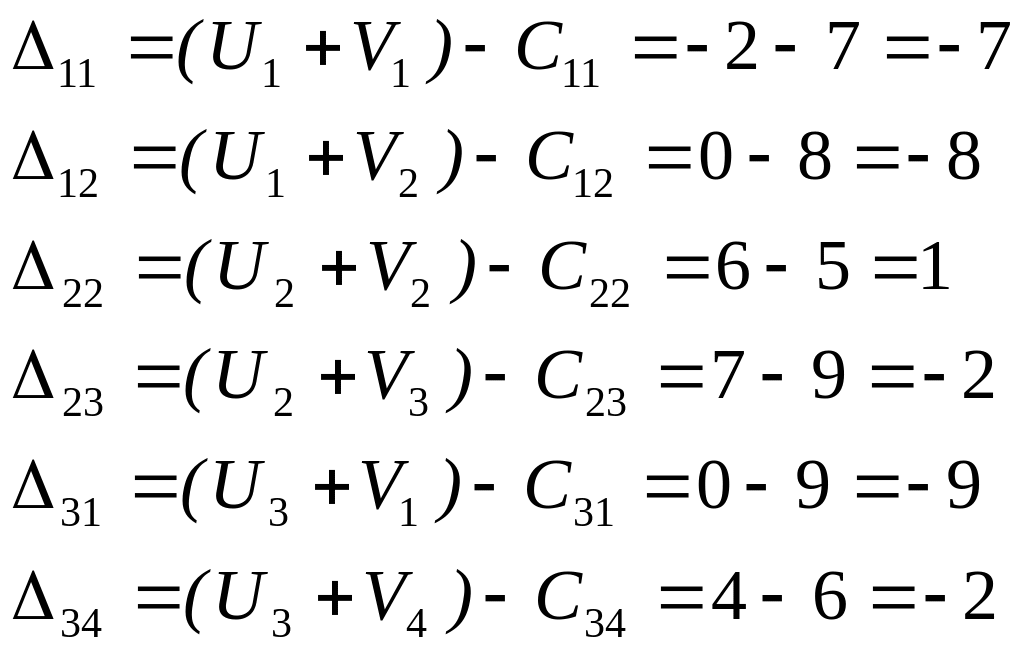
4.3 Получена положительная разность ![]() . Заполним клетку (2,2). Цикл будет содержать клетки (2,2), (3,2), (3,3), (1,3), (1,4), (2,4), (2,2).
. Заполним клетку (2,2). Цикл будет содержать клетки (2,2), (3,2), (3,3), (1,3), (1,4), (2,4), (2,2).
Для того, чтобы не загромождать таблицу цикл можно вынести отдельно:
|
|
| 70 |
|
| 90 |
|
|
|
| – | + |
|
|
|
|
|
| – |
|
|
| + |
|
|
| 20 |
|
| – | + |
|
|
|
| 50 |
|
| 120 |
|
|
Минимальное значение х24=20 для клеток со знаком « - ». Перераспределив продукцию по циклу, получим новый план перевозок, представленный в таблице:
| № | 1 | 2 | 3 | 4 | Предложение |
| 1 | 7 | 8 | 50 1 | 110 2 | 160 |
| 2 | 120 4 | 20 5 | 9 | 8 | 140 |
| 3 | 9 | 30 2 | 140 3 | 6 | 170 |
| Спрос | 120 | 50 | 190 | 110 |
|
5) Полученный план невырожденный. Проверим на оптимальность.
5.1 U1+V3=1, U1=0, V1=-1,
U1+V4=2, U2=5, V2=0,
U2+V1=4, U3=2. V3=1,
U2+V2=2, V4=2.
U3+V2=2,
U3+V3=3.
5.2 Составим разности для свободных клеток:
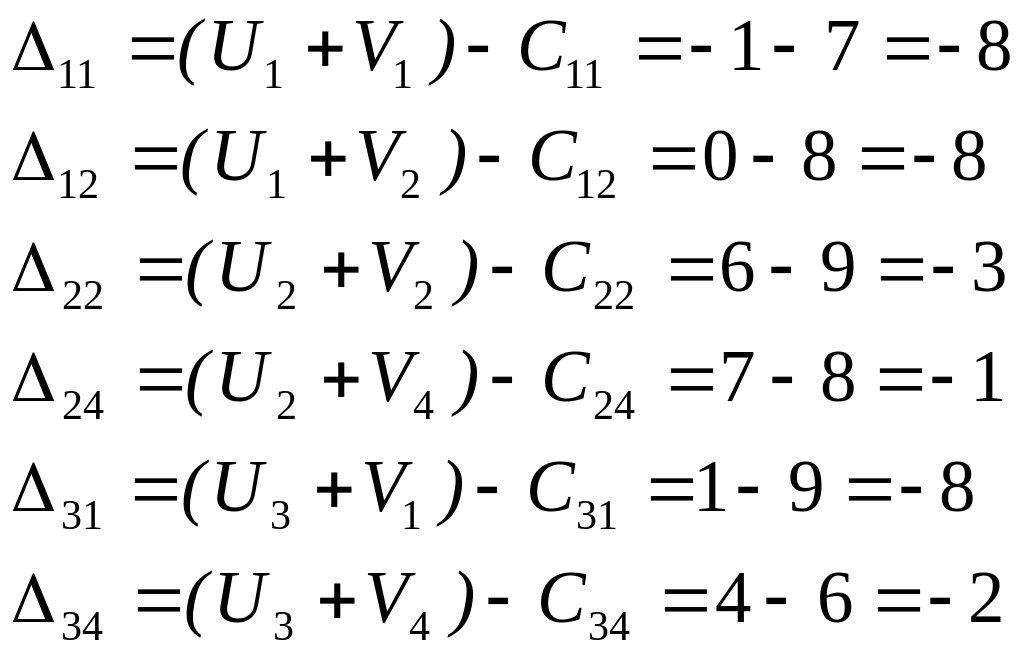
Все разности отрицательные, следовательно полученный план является оптимальным.
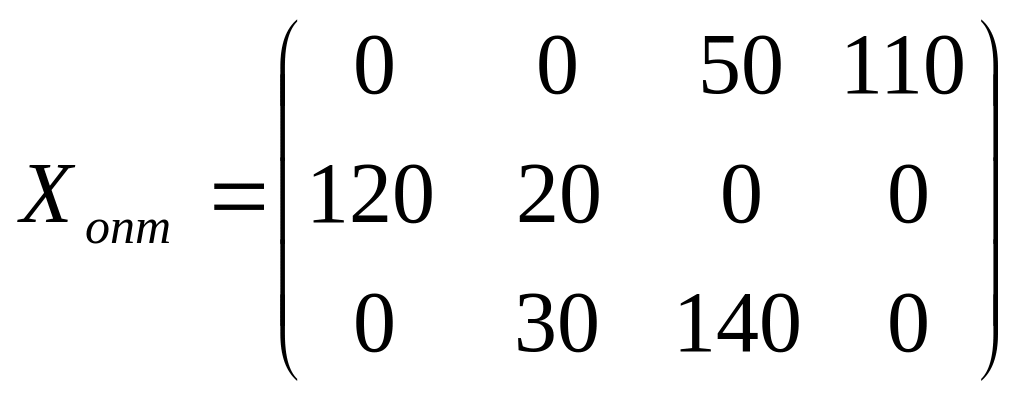
Стоимость перевозки: Lmin=50·1+110·2+120·4+20·5+30·2+140·3=1330 у.е.
Пример 2.
Три торговых склада могут поставлять некоторое изделие в количестве 9,4 и 8 тонн. Величины спроса трех магазинов розничной торговли на это изделие равны 3, 5 и 6 т.
Какова минимальная стоимость транспортировки от поставщиков к потребителям, если матрица стоимостей имеет вид 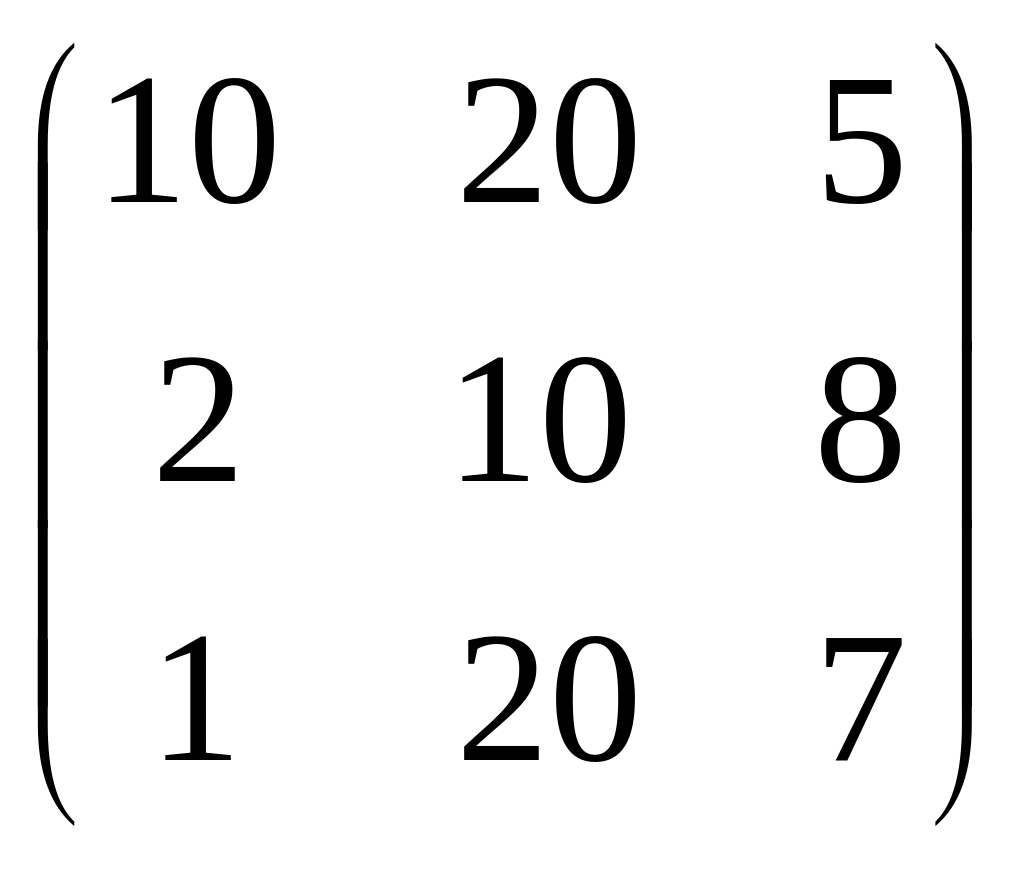 ?
?
Решение: Запасы складов ![]() потребности магазинов:
потребности магазинов: ![]() - задача открытая. Введем фиктивный магазин со спросом
- задача открытая. Введем фиктивный магазин со спросом ![]() и тарифом 20 у.е. и решим задачу методом минимального элемента.
и тарифом 20 у.е. и решим задачу методом минимального элемента.
| № | 1 | 2 | 3 | 4ф | Предложение | ui |
| 1 | 10 | 1 20 | 6 5 | 2 20 | 9 | 0 |
| 2 | 2 | 4 10 | 8 | 20 | 4 | -10 |
| 3 | 3 1 | 20 | 7 | 5 20 | 8 | 0 |
| Спрос | 3 | 5 | 6 | 7 |
|
|
| vj | 1 | 20 | 5 | 20 |
|
|
Оптимизируем полученное решение:
Найдем потенциалы заполненных клеток. (см. таблицу);
Оценим свободные клетки: ![]() .
.
Видим, что положительных оценок нет, значит, полученное решение является оптимальным.
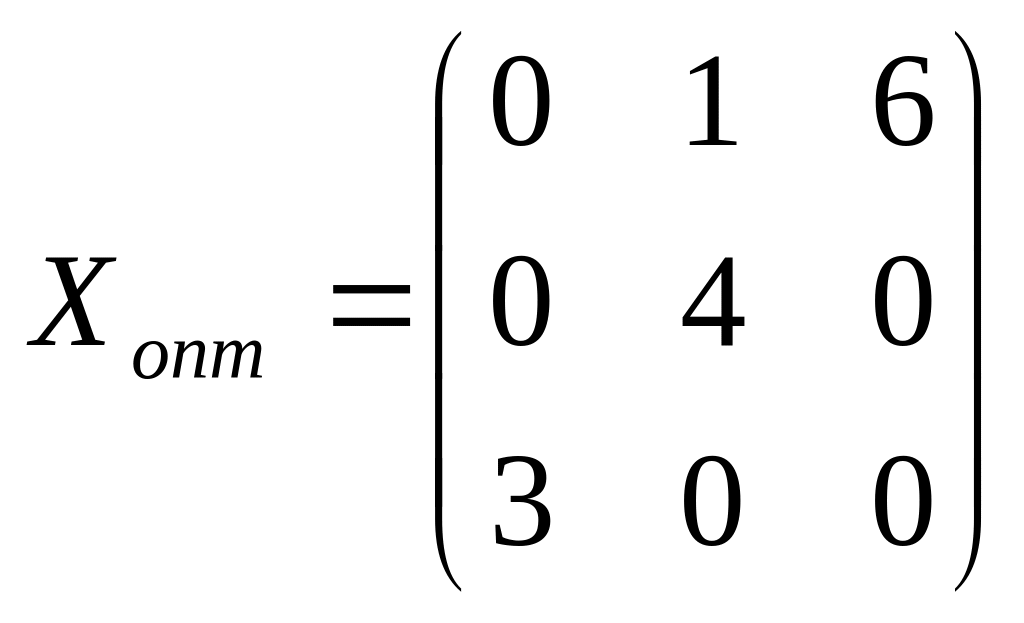 .
.
Минимальная стоимость транспортных расходов Lопт=93 у.е.
Вырожденность в транспортных задачах
При решении транспортной задачи может оказаться, что число занятых клеток меньше, чем m+n-1. В этом случае задача имеет вырожденное решение. Для возможного его исключения целесообразно поменять местами поставщиков и потребителей или ввести в свободную клетку с наименьшим тарифом нулевую поставку. Нуль помещают в такую клетку, чтобы в каждой строке и в каждом столбце было не менее одной занятой клетки.
Пример.
Фирма осуществляет поставку бутылок на три завода, занимающиеся производством прохладительных напитков. Она имеет три склада, причем на складе 1 находится 6000 бутылок, на складе 2 – 3000 бутылок и на складе 3 - 4000бутылок. Первому заводу требуется 4000бутылок, второму – 5000 бутылок, третьему – 1000 бутылок. Стоимость перевозки одной бутылки от каждого склада к каждому заводу задана матрицей:
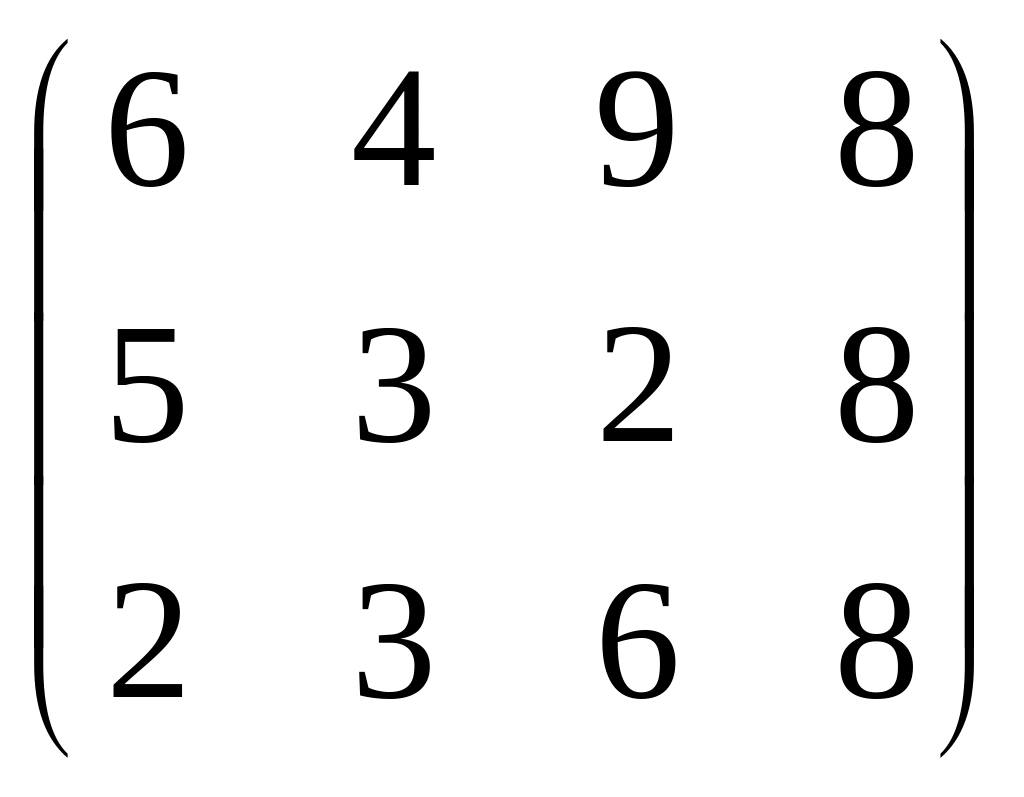
Как следует организовать доставку бутылок на заводы, чтобы стоимость перевозки была минимальной?
Решение:
1.1 Запишем данные в распределительную таблицу.
1.2 Найдем опорное решение методом минимального тарифа.
1.3 Проверим вырожденной или невырожденной является транспортная задача: m+n-1=3+4-1=6, а число заполненных клеток равно 5, следовательно, задача является вырожденной (см. определение).
| № | 1 | 2 | 3 | 4 | Предложение | ui |
| 1 | 6 | 3000 4 | 9 | 3000 8 | 6000 | 0 |
| 2 | 5 | 2000 3 | 1000 2 | 8 | 3000 | -1 |
| 3 | 4000 2 | 0 3 | 6 | 8 | 4000 | -1 |
| Спрос | 4000 | 5000 | 1000 | 3000 |
|
|
| vj | 3 | 4 | 3 | 8 |
|
|
Исключим вырожденность. Для этого:
1. Введем в какую–нибудь клетку нулевую поставку. Такая клетка становится условно занятой. Ее целесообразно определить при вычислении потенциалов занятых клеток, она должна иметь наименьший тариф по сравнению с другими клетками, которые могут быть условно занятыми.
2.1.2. Определим потенциалы занятых клеток:
u1+v2=4, u1+v4=8, u2+v2=3, u2+v3=2, u3+v1=2.
Полагая, что u1=0 находим v2=4, u2=-1,v3=3.
Для того чтобы найти u3 и v1 поместим нулевую поставку в клетку (3,2), и из равенства u3+v2=0 найдем сначала u3, затем v1.
3.1. Составим разности для свободных клеток:
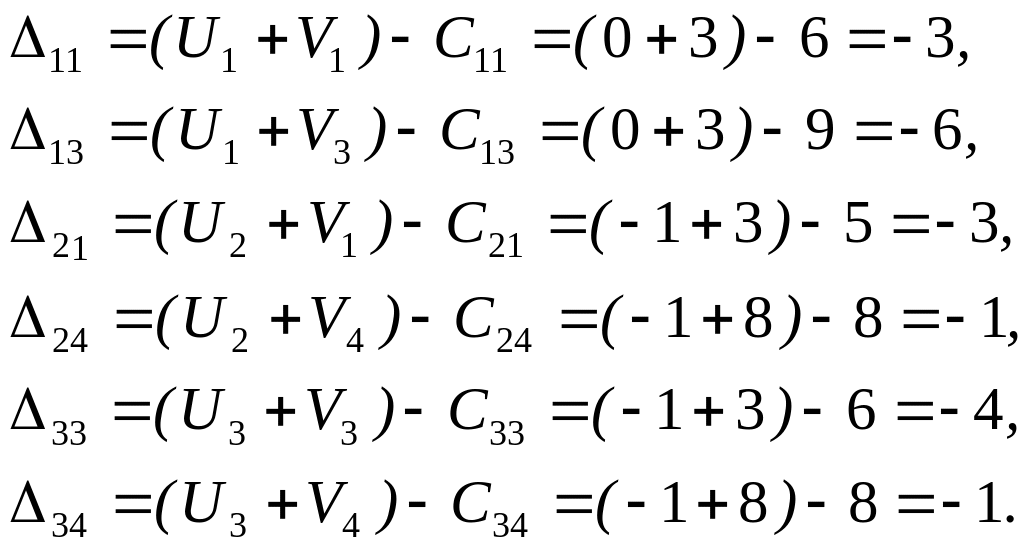
Все оценки отрицательные, значит полученное начальное решение является оптимальным.
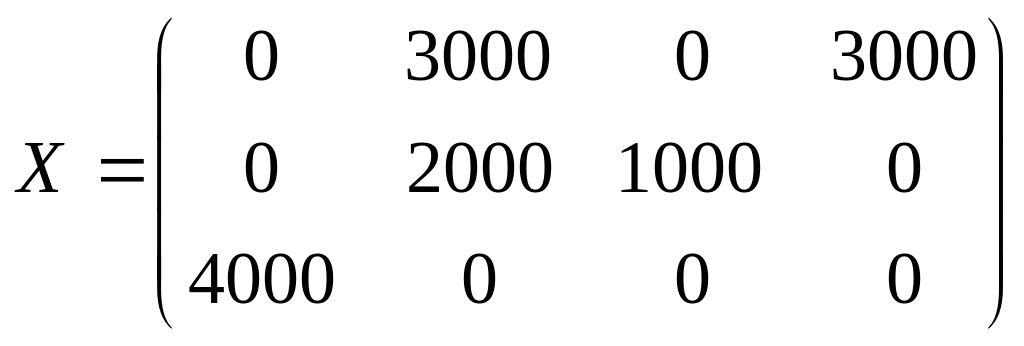
![]()
Таким образом, со склада 1 целесообразно поставить 3000 бутылок второму и четвертому заводам, со склада 2 – 2000 бутылок второму заводу и 1000 бутылок третьему, со склада 3 – 4000 бутылок первому заводу, при этом стоимость транспортных расходов будет минимальной и составит 28000 у.е.
Приложения транспортных моделей
Алгоритм и методы решения транспортных задачи могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов Cij имеют различный смысл в зависимости от конкретной экономической задачи. К таким задачам относятся следующие:
- оптимальное закрепление за станками операций по обработке деталей. В них Cij является таким экономическим показателем, как производительность. Задача позволяет определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей. Так как транспортная задача требует нахождения минимума, то значения Сij берутся с отрицательным знаком;
- оптимальные назначения или проблема выбора. Имеется m механизмов, которые могут выполнять m различных работ с производительностью Сij. Задача позволяет определить, какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности;
- задача о сокращении производства с учетом суммарных расходов на изготовление и транспортировку продукции;
- решение задач с помощью метода запрещения перевозок. Используется в том случае, если груз от некоторого поставщика по каким – то причинам не может быть направлен одному из потребителей. Данное ограничение можно учесть, присвоив соответствующей клетке достаточно большое значение стоимости, тем самым в эту клетку не будут производиться перевозки.
Выбор оптимального варианта использования
производственного оборудования
На предприятии имеются три группы станков, каждая из которых может выполнять пять операций по обработке деталей (операции могут выполняться в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250, 180 ч. Каждая операция должна выполняться соответственно 100, 120, 70, 130 ч.
Определить, сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество деталей.
Производительность каждой группы станков на каждую операцию задана матрицей
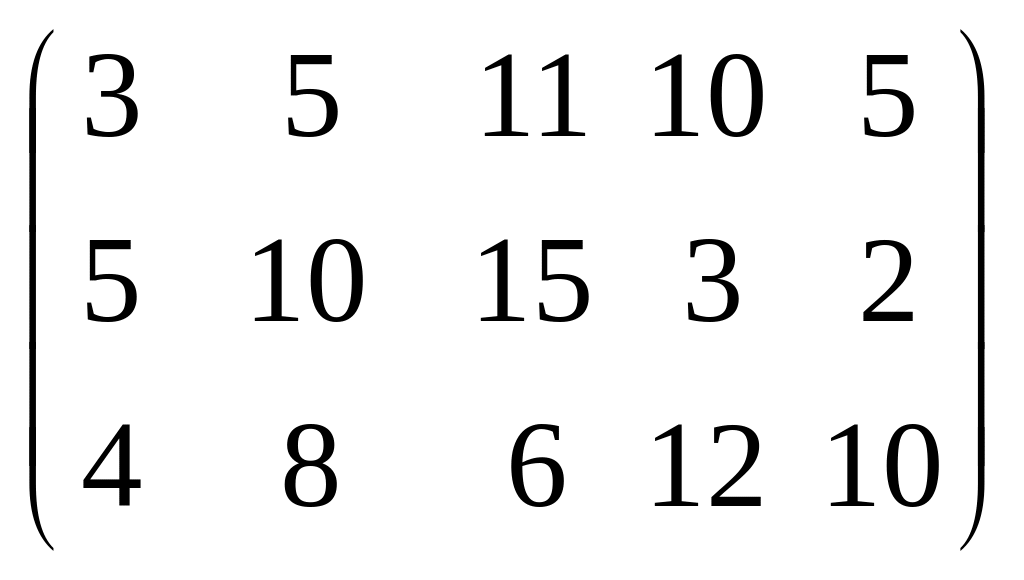
![]()
Решение. Воспользуемся алгоритмом решения закрытой транспортной задачи .
Так как в задаче требуется найти максимум, а согласно алгоритму транспортной задачи находится минимум, тарифы умножим на (—1).
| № | 1 | 2 | 3 | 4 | 5 |
| ui |
| 1 | -3 40 | -5 | -11 | -10 | -5 60 |
100
|
0 |
| 2 | -5 60 | -10 120 | -15 70 | -3 | -2 | 250 | -2
|
| 3 | -4
| -8 | -6 | -12 110 | -10 70 | 180 | -5 |
|
| 100 | 120 | 70 | 110 | 130 |
|
|
| VJ | -3 | -8 | -13 | -7 | -5 |
|
|
Находим потенциалы свободных клеток:
![]() .
.
Так как ![]() , перераспределим грузы, получим
, перераспределим грузы, получим
|
|
|
| 60 | 60 |
|
|
|
|
| + | – |
|
|
|
|
|
|
| – | + |
|
|
|
|
|
| 110 |
|
| 70 | 50 |
|
| 130 |
Полученное перераспределение грузов занесем в таблицу.
| № | 1 | 2 | 3 | 4 | 5 |
| ui |
| 1 | -3 40 | -5 | -11 | -10 60 | -5
|
100
|
0 |
| 2 | -5 60 | -10 120 | -15 70 | -3 | -2 | 250 | -2
|
| 3 | -4
| -8 | -6 | -12 50 | -10 130 | 180 | -2 |
|
| 100 | 120 | 70 | 110 | 130 |
|
|
| VJ | -3 | -8 | -13 | -10 | -8 |
|
|
Оценки свободных клеток составляют:
![]()
Найденное решение является оптимальным, так как все оценки свободных клеток отрицательные.
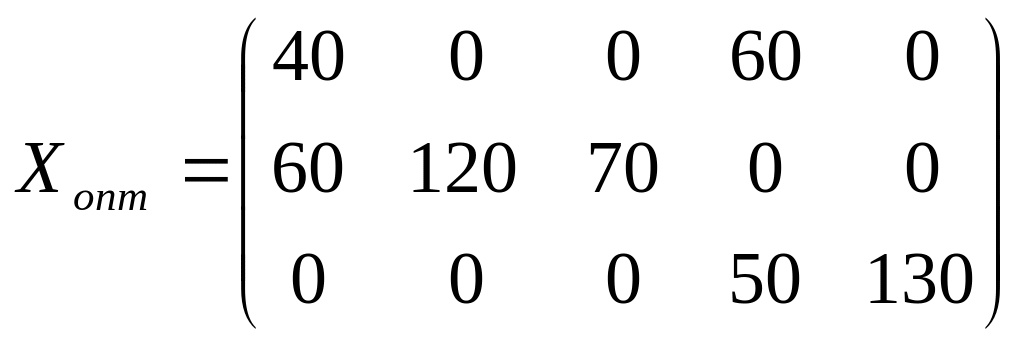 .
.
Таким образом, на первой группе станков целесообразно выполнять операции 1 и 4 продолжительностью 40 и 60 часов соответственно, на второй группе – операции 1,2 и 3 продолжительностью 60,120 и 70 часов соответственно. При этом максимальное количество обработанных деталей составит 5170 штук.
Решение транспортной задачи средствами MathCAD.
Решение транспортной задачи можно осуществить средствами MathCAD. Для этого необходимо, чтобы транспортная задача была закрытой. Так как одним из самых эффективных методов решения транспортной задачи является метод потенциалов, рассмотрим, как можно осуществить алгоритм этого метода с помощью пакета MathCAD.
Пример.
Дана транспортная задача (в виде таблицы). Найти ее исходное решение.
| № | В1 | В2 | В3 | Предложение |
| А1 | 70 | 38 | 24 | 14 |
| А2 | 58 | 18 | 56 | 20 |
| А3 | 19 | 10 | 100 | 26 |
| Спрос | 30 | 22 | 8 |
|
![]() т.
т.
Решение:
Исходный план будет состоять из 9-ти чисел ( для данной задачи):
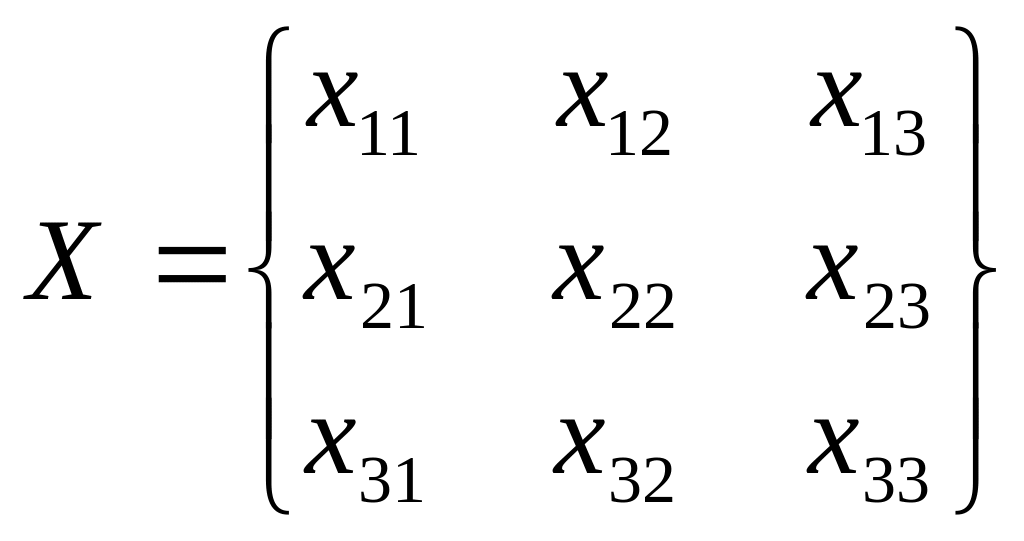 , где
, где ![]() - количество единиц груза, которое необходимо перевезти из пункта i в пункт j.
- количество единиц груза, которое необходимо перевезти из пункта i в пункт j.
Математическая модель такой задачи имеет вид:
Целевая функция:
![]()
![]()
Системы равенств:
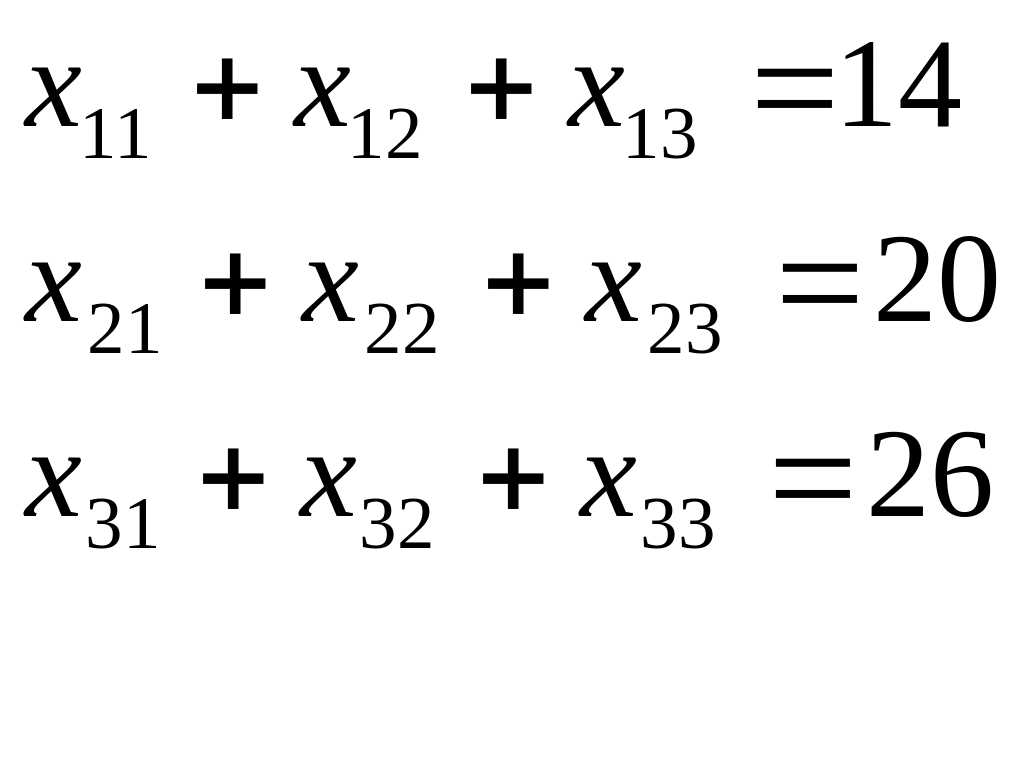
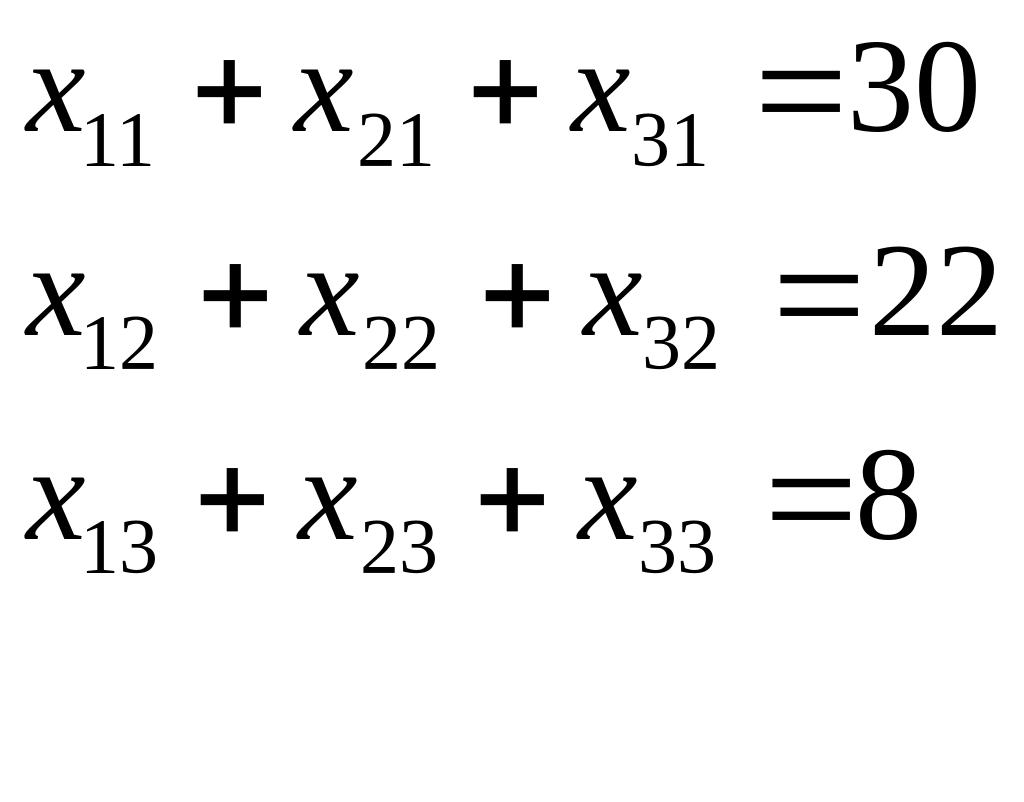
Система ограничений:
![]() , при i=1,2,3; j=1,2,3.
, при i=1,2,3; j=1,2,3.
Решение транспортной задачи с использованием MathCAD
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
G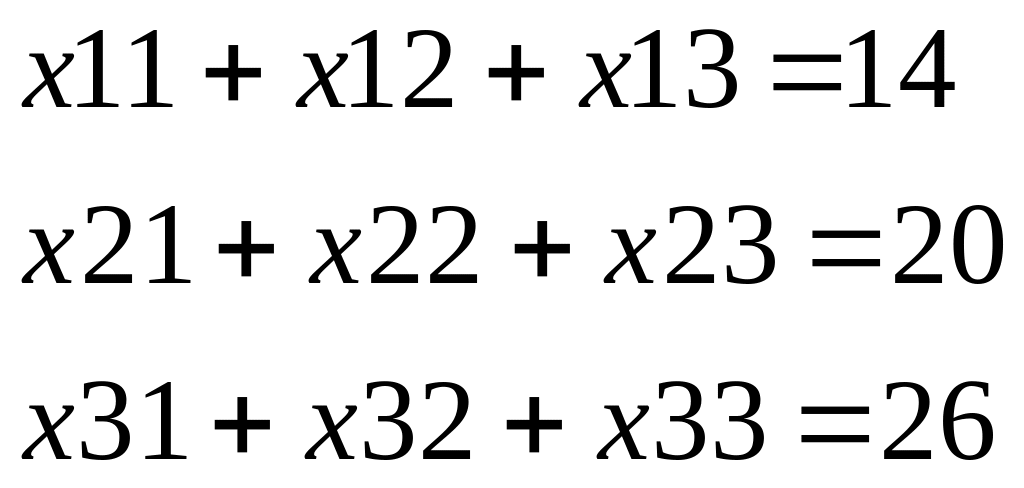
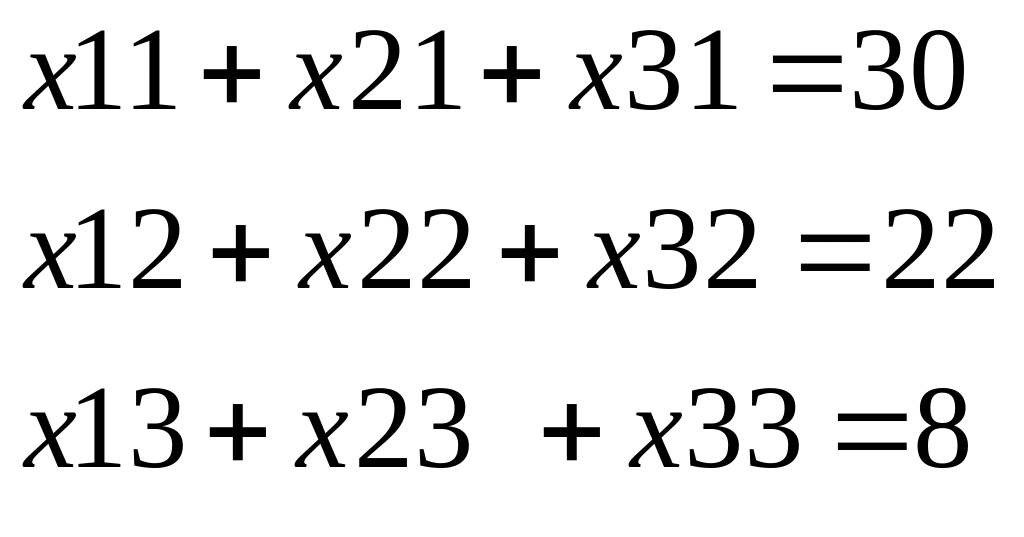 iven
iven
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() : =Minimize (y,
: =Minimize (y, ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() )
)
![]() =
=![]()
(y, ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() )=
)=![]()
Найденное решение означает следующее:
Производимые на предприятия А1 14 единиц продукции следует распределить по складам следующим образом:
склад В1 – 4 единицы;
склад В2 – 2 единицы;
склад В3 – 8 единиц.
Производимые на предприятии №2 20 единиц продукции следует распределить по складам следующим образом:
склад В1 – 0 единиц;
склад В2 – 20 единиц;
склад В3 – 0 единиц.
Производимые на предприятии №3 26 единиц продукции следует распределить по складам следующим образом:
склад В1 – 26 единиц;
склад В2 – 0 единиц;
склад В3 – 0 единиц.
Затраты на перевозку всех грузов при таком распределении продукции составят 1402 у.е. и эти затраты являются минимальными.
III раздел
Задача о назначениях
Постановка задачи
Задача заключается в выборе такого распределения ресурсов по объектам, при котором минимизируется стоимость назначений. Предполагается, что каждый ресурс назначается ровно один раз и каждому объекту приписывается ровно один ресурс.
Возможные применения задачи о назначениях представлены в таблице:
| Ресурсы | Объекты | Критерии эффективности |
| Рабочие | Рабочие места | Время |
| Грузовые автомобили | Маршруты | Затраты |
| Станки | Участки | Объем переработанной продукции |
| Экипажи | Рейсы | Время простоя |
| Коммивояжер | Города | Товарооборот |
Матрица стоимостей имеет вид: ![]() где
где ![]() - затраты, связанные с назначением i-го ресурса на j-ый объект, i=j=1,n, где n-число объектов или ресурсов.
- затраты, связанные с назначением i-го ресурса на j-ый объект, i=j=1,n, где n-число объектов или ресурсов.
Обозначим:
![]()
Таким образом, решение задачи может быть записано в виде ![]() .
.
Допустимое решение называется назначением. Оно строится путем выбора ровно одного элемента в каждой строке матрицы ![]() и ровно одного элемента в каждом столбце этой матрицы.
и ровно одного элемента в каждом столбце этой матрицы.
Элементы ![]() матрицы С, соответствующие элементам
матрицы С, соответствующие элементам ![]() матрицы X, будем отмечать кружками:
матрицы X, будем отмечать кружками:
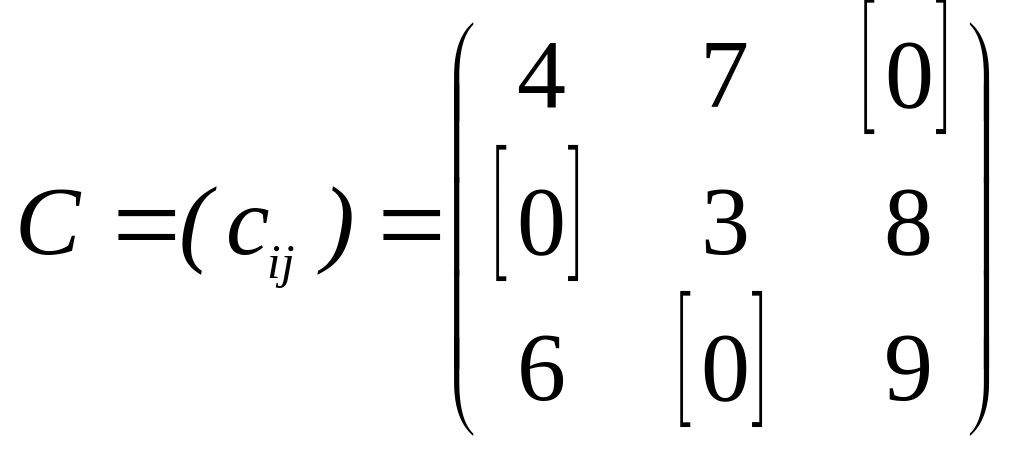 ,
, 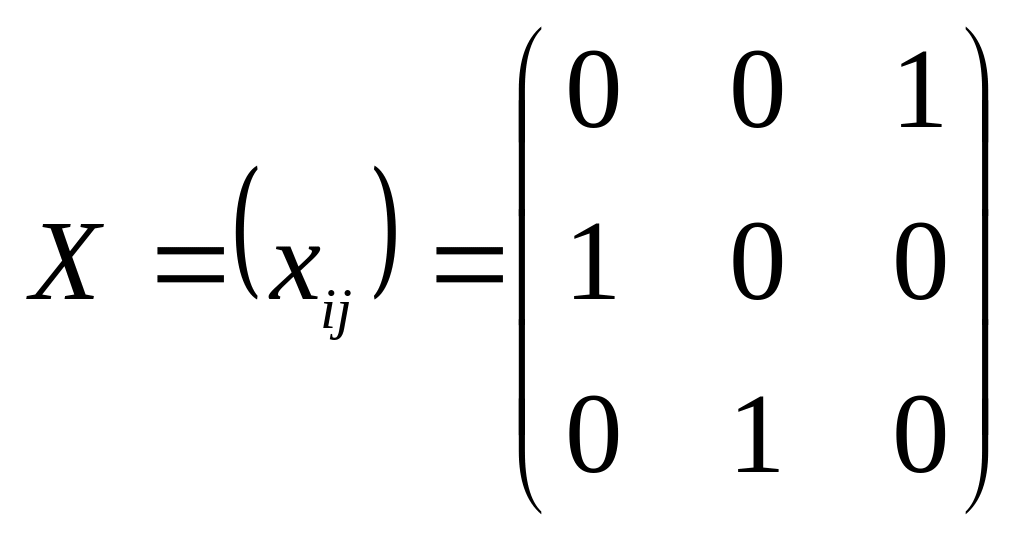 .
.
Математическая постановка задачи:
![]() при ограничениях:
при ограничениях: 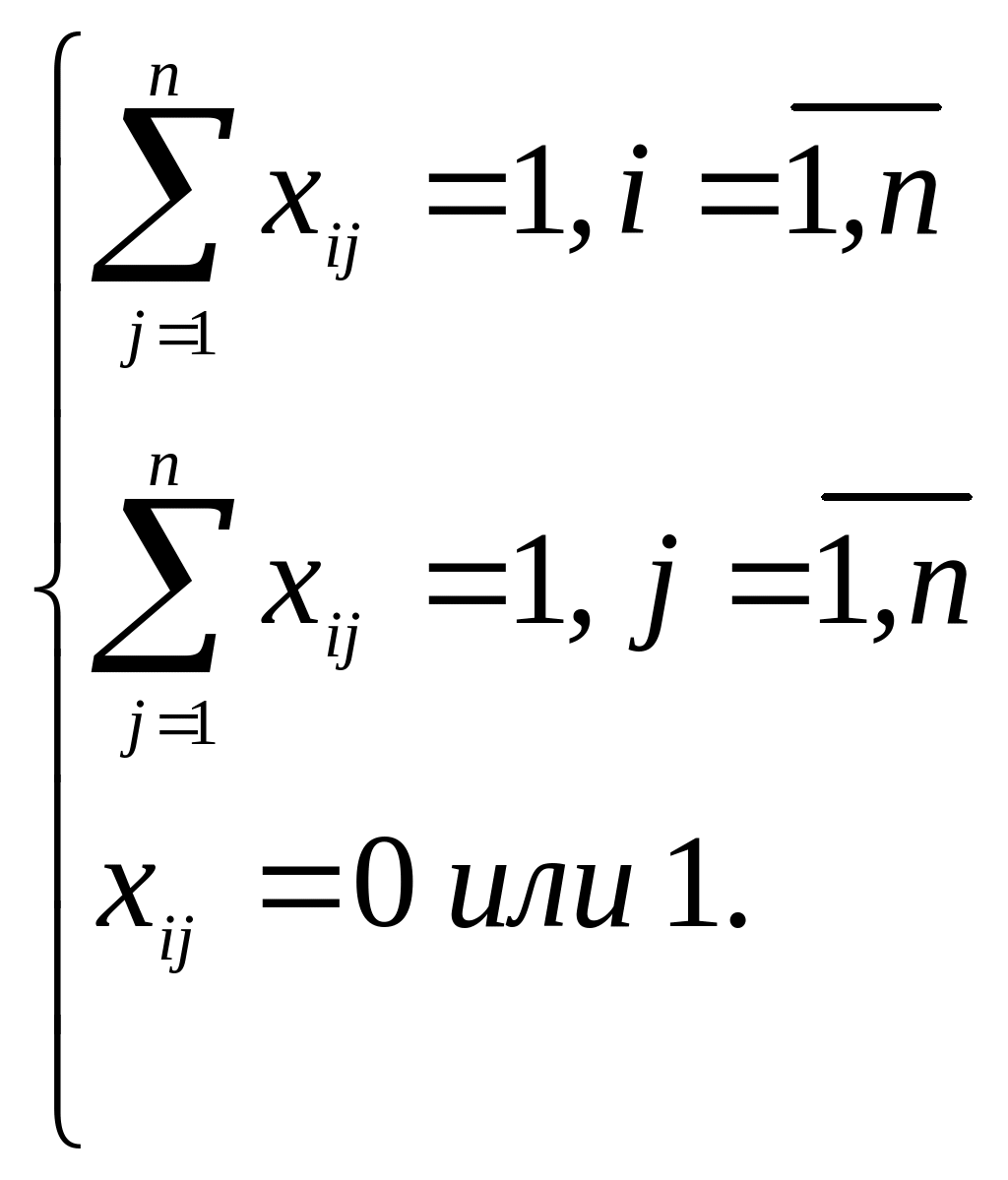
Алгоритм решения задачи
Задача о назначениях является частным случаем транспортной задачи, в которой ![]() Поэтому ее можно решать алгоритмами транспортной задачи. Рассмотрим другой метод, который является более эффективным, учитывающим специфику математической модели. Этот метод называется венгерским алгоритмом. Он состоит из следующих шагов:
Поэтому ее можно решать алгоритмами транспортной задачи. Рассмотрим другой метод, который является более эффективным, учитывающим специфику математической модели. Этот метод называется венгерским алгоритмом. Он состоит из следующих шагов:
преобразования строк и столбцов матрицы;
определение назначения;
модификация преобразованной матрицы.
1 шаг. Цель: получение максимально возможного числа нулевых элементов в матрице С. Для этого из всех элементов каждой строки вычитаем минимальный элемент соответствующей строки, а из всех элементов каждого столбца вычитаем минимальный элемент соответствующего столбца.
2 шаг. Если после выполнения 1-го шага в каждой строке и в каждом столбце матрицы С можно выбрать по одному нулевому элементу, то полученное решение будет оптимальным назначением.
3шаг. Если допустимое решение, состоящее из нулей, не найдено, то проводим минимальное число прямых через некоторые столбцы так, чтобы все нули оказались вычеркнутыми. Выбираем наименьший невычеркнутый элемент. Этот элемент вычитаем из каждого невычеркнутого элемента и прибавляем к каждому элементу, стоящему на пересечении проведенных прямых.
Если после проведения 3-го шага оптимальное решение не достигнуто, то процедуру проведения прямых следует повторить до тех пор пока не будет получено допустимое решение.
Пример:
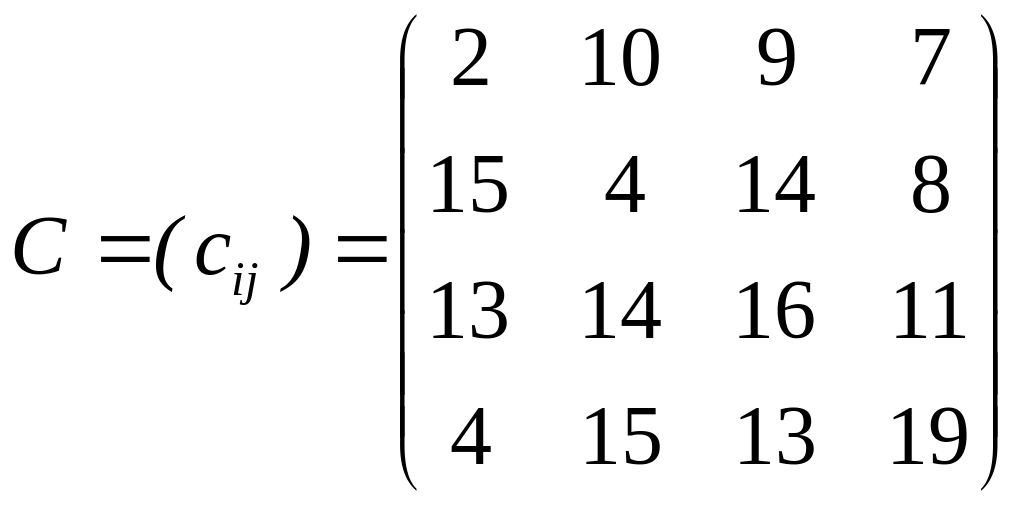 .
.
Распределить ресурсы по объектам.
Решение. 1шаг. Значения минимальных элементов строк1,2,3 и 4 равны 2, 4, 11 и 4 соответственно. Вычитая, из элементов каждого столбца соответствующее минимальное значение, получим:
![]()
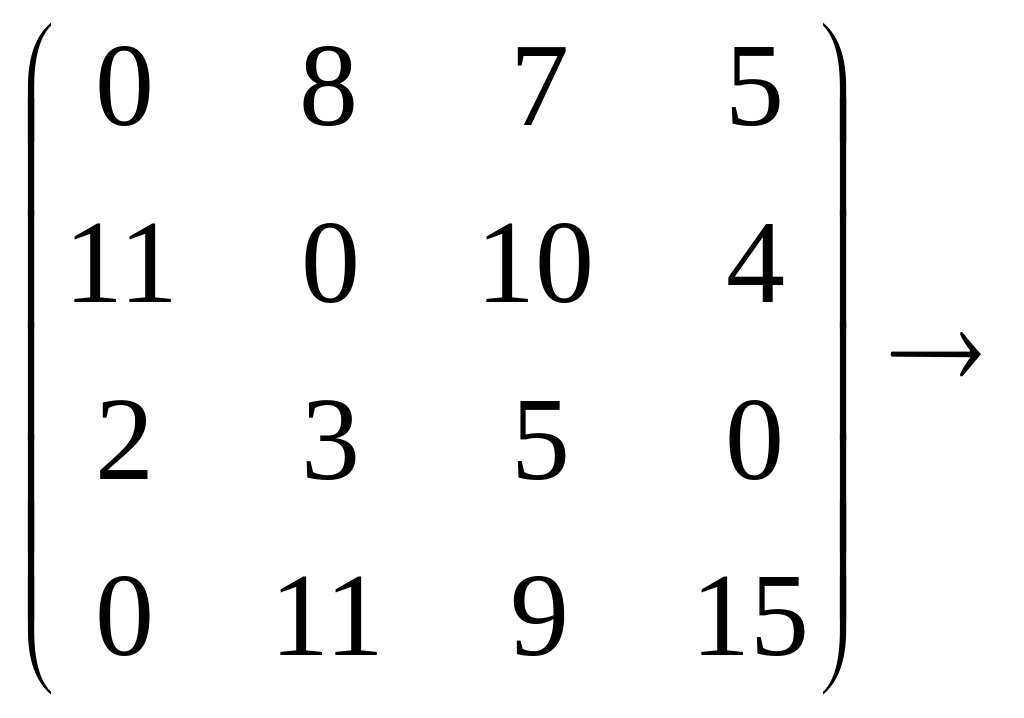

Значения минимальных элементов столбцов 1, 2, 3 и 4 равны 0, 0, 5, 0 соответственно. Вычитая из элементов каждого столбца соответствующее минимальное значение, получим: 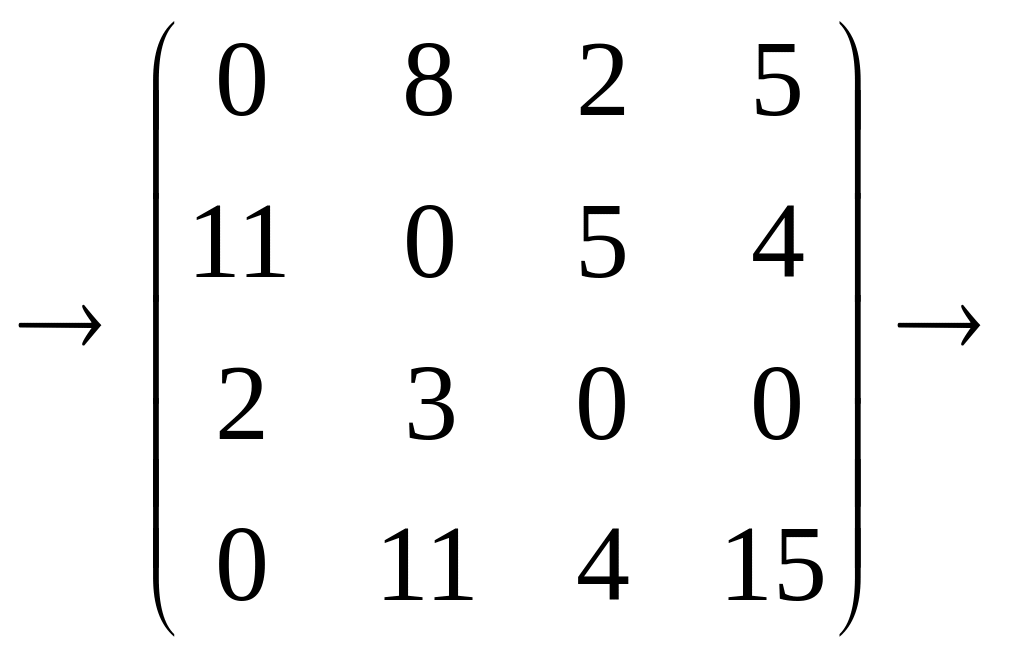
2 шаг: Ни одно полное назначение не получено, необходимо провести модификацию матрицы стоимостей.
3 шаг: Вычеркиваем столбец 1, строку 3, строку 2 (или столбец 2). Значение минимального невычеркнутого элемента равно 2:
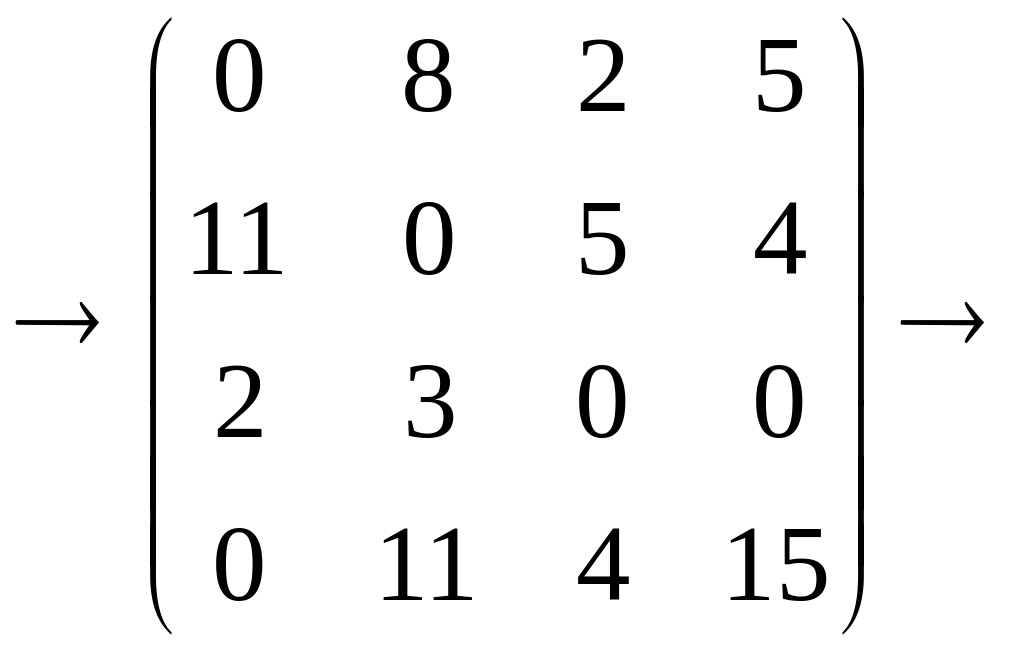 min=2.
min=2.
Вычитаем его из всех невычеркнутых элементов и, складывая его со всеми элементами, расположенными на пересечении двух линий, получим:
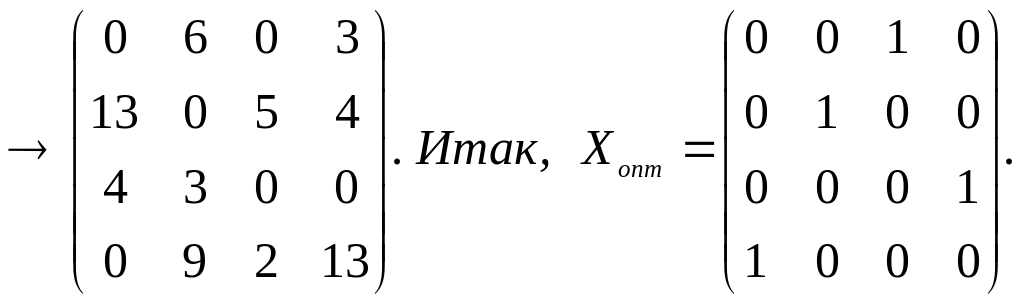
Примечания
1. Если исходная матрица не является квадратной, то нужно ввести фиктивные ресурсы или фиктивные объекты, чтобы матрица стала квадратной.
2. Если какой-либо ресурс не может быть назначен на какой –то объект, то соответствующая стоимость полагается равной достаточно большому числу М.
3. Если исходная задача является задачей максимизации, то все элементы матрицы С следует умножить на (-1) и сложить их с достаточно большим числом так, чтобы матрица не содержала отрицательных элементов. Затем задачу следует решить как задачу минимизации.(например, задача о планировании загрузки оборудования с учетом максимальной производительности станков)
4. Если число линий, необходимое для того, чтобы вычеркнуть нулевые элементы, равно числу строк или столбцов (квадратной матрицы), то существует назначение нулевой стоимости.
IVраздел
Симплекс – метод
Симплекс – метод – универсальный метод для решения задач линейного программирования, представленных в канонической форме.
В канонической форме записи все переменные неотрицательны, ограничениями являются уравнения, и требуется найти такие значения переменных xj, j=1,n, при которых целевая функция имеет максимум:
![]()
![]()
![]()
Переход к канонической форме записи можно осуществить с помощью следующих действий:
Ограничения вида «». В этом случае, для перехода к уравнению в левую часть неравенства добавляют дополнительную неотрицательную переменную.
Ограничения вида «» . В этом случае, для перехода к соответствующему уравнению, вычитают из левой части дополнительную неотрицательную переменную.
Если в задаче какая – либо из переменных произвольна, то от нее избавляются, заменяя ее разностью двух других неотрицательных переменных. Например, для произвольной переменной ![]() , где
, где ![]() .
.
Если в задаче требуется найти минимум f , то заменяя f на – f, переходят к задаче максимизации, так как ![]() .
.
Алгоритм симплекс- метода
Приводим математическую модель задачи к каноническому виду ( в случае неканонической).
Находим начальное решение и проверяем его на оптимальность.
Получение начального решения:
Выбираются m переменных, называемых базисными и обладающих следующим свойством: они входят с коэффициентом 1 только в одно уравнение и с коэффициентом 0 в остальные уравнения системы :
![]() (1)
(1)
![]()
Остальные n-m переменных называются свободными.
Все свободные переменные полагаются равными нулю, а базисные переменные – равные правым частям соответствующих ограничений системы (1).
Если все ![]() , то начальное решение является допустимым.
, то начальное решение является допустимым.
3. Выражение функции f только через свободные переменные:
![]() .
.
4. Проверка решения на оптимальность.
Для этого составляется симплекс- таблица:
| Базисные переменные | Коэффициенты при переменных | Свободные члены | |||||||
|
| X1 | X2 | … | Xm | … | XP | … | Xn |
|
| X1 | a11 | a12 | … | a1m | … | a1p | … | a1n | b1 |
| X2 | a21 | a22 | … | a2m | … | a2p | … | a2p | b2 |
| … | … | … | … | … | … | … | … | … | … |
| Xq | aq1 | aq2 | … | aqm | … | aqp | … | aqn | bq |
| … | … | … | … | … | … | … | … | … | … |
| Xm | am1 | am2 | … | amm | … | amp | … | amn | bm |
| f | -c1 | -c2 | … | -cm | … | -cp | … | -cn | 0 |
Для проверки решения на оптимальность просматривается последняя f-строка:
4.1 Если коэффициенты, стоящие при свободных переменных неотрицательны, то полученное решение оптимально.
4.2 Если все эти коэффициенты положительны, то полученное решение единственно.
4.3 Если среди неотрицательных коэффициентов встречается хотя бы один нулевой, то задача имеет бесконечное множество решений.
4.4 Если в последней строке есть хотя бы один отрицательный коэффициент, а в соответствующем этому коэффициенту столбце нет ни одного положительного элемента, то целевая функция не ограничена в области допустимых решений. (решение прекращаем).
4.5 Если хотя бы один из коэффициентов, стоящих при свободных переменных, отрицательный и в соответствующем ему столбце есть хотя бы один положительный элемент, то полученное решение может быть улучшено.
5. Получение нового решения.
5.1 Выбор переменной, вводимой в список базисных переменных.
Просматривается последняя строка симплекс- таблицы. Среди элементов этой строки выбирается минимальный элемент. Столбец, в котором стоит этот элемент, называется разрешающим. Переменная, стоящая в этом столбце вводится в список базисных переменных.
5.2. Выбор переменной, выводимой из списка базисных переменных.
Находят отношение элементов столбца свободных членов к элементам разрешающего столбца. При делении на отрицательный элемент и 0 результат полагают равным +∞. Среди отношений находят минимальное. Строка соответствующая минимальному отношению, называется разрешающей. Базисная переменная, стоящая в этой строке, выводится из списка базисных переменных. Элемент, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом.
5.3.Выполнение симплекс-преобразования и переход к новой симплекс- таблице.
П
 ереписываем разрешающую строку, разделив ее на ключевой элемент; остальные коэффициенты таблицы находим по правилу «прямоугольника»: новый элемент = (старый элемент)×(разрешающий элемент) - × .
ереписываем разрешающую строку, разделив ее на ключевой элемент; остальные коэффициенты таблицы находим по правилу «прямоугольника»: новый элемент = (старый элемент)×(разрешающий элемент) - × .
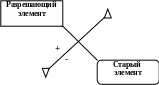
Элемент  находится в разрешающей строке в одном столбце со старым элементом. Элемент
находится в разрешающей строке в одном столбце со старым элементом. Элемент  находится в разрешающем столбце в одной строке со старым элементом.
находится в разрешающем столбце в одной строке со старым элементом.
Получаем новое опорное решение, которое снова проверяем на оптимальность и т.д. по рассмотренному алгоритму, пока не получим оптимальное решение.
Пример.
Анализ эффективности использования производственного потенциала предприятия.
Предприятие располагает тремя производственными ресурсами (сырьем, электроэнергией, оборудованием) и может организовать производство продукции двумя различными способами. Расход ресурсов за один месяц и общий ресурс при каждом способе производства даны в таблице ( в у.е.)
| Производственные ресурсы | Расход ресурсов за 1 месяц при работе | Общий ресурс | |
| 1-м способом | 2-м способом | ||
| Сырье | 1 | 2 | 4 |
| Оборудование | 1 | 1 | 3 |
| Электроэнергия | 2 | 1 | 8 |
При первом способе производства предприятие выпускает за 1 месяц – 3 тыс. изделий, при втором – 4 тыс. изделий.
Сколько месяцев должно работать предприятие каждым из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции?
Решение: Пусть ![]() - время работы предприятия 1-м способом,
- время работы предприятия 1-м способом, ![]() - вторым способом.
- вторым способом.
Математическая модель задачи имеет вид:
![]()
![]() max, при ограничениях:
max, при ограничениях:
![]()
![]()
Приведем задачу к каноническому виду:
![]()
![]() max, при ограничениях:
max, при ограничениях:
![]()
![]()
Решение:
Составляем симплекс – таблицу 1-го шага:
| Базис | Свободные члены |
|
|
|
|
|
|
| 4 | 1 | 2 | 1 | 0 | 0 |
|
| 3 | 1 | 1 | 0 | 1 | 0 |
|
| 8 | 2 | 1 | 0 | 0 | 1 |
| f | 0 | -3 | -4 | 0 | 0 | 0 |
Решение (0;0;4;3;8), L(x) = 0
Видим, что в последней строке таблицы есть отрицательные числа - переходим к пункту 2.
2)Выбираем столбец, содержащий максимальное положительное число – 4 и отмечаем его. Переходим к пункту 3.
3)Делим, свободные члены на соответствующие положительные числа из выделенного столбца и выбираем наименьшее частное:
min![]() =(4;3;2)=2
=(4;3;2)=2
Отмечаем строку таблицы, которая соответствует наименьшему частному. Выделяем разрешающий элемент равный 2.
4) Делим элементы выделенной строки на этот элемент и начинаем заполнять новую таблицу.
| Базис | Свободные члены |
|
|
|
|
|
|
| 2 | 1/2 | 1 | 1/2 | 0 | 0 |
|
| 1 | 1/2 | 0 | -1/2 | 1 | 0 |
|
| 6 | 3/2 | 0 | -1/2 | 0 | 1 |
| f | 8 | -1 | 0 | 2 | 0 | 0 |
Переходим снова к шагу 1.
| Базис | Свободные члены |
|
|
|
|
|
|
| 1 | 0 | 1 | 1 | -1 | 0 |
|
| 2 | 1 | 0 | -1 | 2 | 0 |
|
| 3 | 0 | 0 | 1 | -3 | 1 |
| f | 10 | 0 | 0 | 1 | 2 | 0 |
min![]() =(4;3;2)=2
=(4;3;2)=2
Все коэффициенты в строке f положительные, значит оптимальное решение получено. X опт = (2;1;0;0;3) , f= 3*2+4=10. Таким образом, по 1-ому способу предприятие должно работать 2 месяца, по 2-ому – 1 месяц, при этом максимальный выпуск продукции составит 10 тыс. рублей.
Приложение 1
Контрольные задания по теме
«Графический метод»
1. На некотором предприятии могут выпускать изделия двух видов (например, мотоциклы и велосипеды). В силу ограниченности возможностей сборочного цеха в нем могут собирать за день 25 мотоциклов (если не собирать вообще велосипеды) или 100 велосипедов (если не собирать вообще мотоциклов), либо какую-то комбинацию тех и других, определяемую приемлемыми трудозатратами. Склад может принять не более 70 изделий любого вида в сутки. Известно, что мотоцикл стоит в 2 раза дороже велосипеда. Требуется найти такой план выпуска продукции, который обеспечил бы предприятию наибольшую выручку.
2. В суточный рацион включают 2 продукта питания П1 и П2, причем продуктаП1 должно войти в дневной рацион не более 200 ед. Стоимость 1 ед. продукта П1составляет 2у.е., продукта П2 – 4р. Содержание питательных веществ в 1 ед. продукта, минимальные нормы потребления указаны в таблице. Определить оптимальный рацион питания, стоимость которого будет наименьшей. Решить задачу графическим методом.
| Питательные вещества | Минимальная норма потребления | Содержание питательных веществ в 1ед. продукта | |
| П1 | П2 | ||
| А | 120 | 0,2 | 0,2 |
| В | 160 | 0,4 | 0,2 |
3. Для производства 2 изделий А и В используются 3 вида сырья. Каждый из них используется в объеме, не превышающем 180, 150 и 630 килограмм соответственно. Нормы затрат каждого из видов сырья на 1 изделие и цена единицы изделий приведены в таблице. Определить план выпуска изделий, обеспечивающий получение максимального дохода.
| Вид сырья | Нормы затрат сырья на одно изделие, кг | |
| А | В | |
| I | 3 | 2 |
| II | 3 | 1 |
| II | 7 | 9 |
| Цена изделия в у.е | 10 | 14 |
4. Фирма выпускает изделия двух типов: А и В. При этом используется сырье четырех видов. Расход сырья каждого вида на изготовление единицы продукции и запасы сырья заданы в таблице:
| Изделия | Сырье | |||
| 1 | 2 | 3 | 4 | |
| А | 2 | 1 | 0 | 2 |
| В | 3 | 0 | 1 | 1 |
Запасы сырья 1-го вида составляют 21 ед., 2-го вида – 4 ед., 3-го вида - 6 ед., 4-го вида – 10 ед. Выпуск одного изделия типа А приносит доход 300 руб., одного изделия типа В – 200 руб. Составить план производства, обеспечивающей фирме наибольший доход.
5. Обработка деталей А и В может производиться на трех станках, причем каждая деталь должна последовательно обрабатываться на каждом из станков. Прибыль от реализации детали А – 100р., детали В – 160 р. Исходные данные приведены в таблице:
| Станки | Норма времени на обработку одной детали, ч | Время работы станка, ч | |
| А | В | ||
| 1 | 0,2 | 0,1 | 100 |
| 2 | 0,2 | 0,5 | 180 |
| 3 | 0,1 | 0,2 | 100 |
Определить производственную программу, максимизирующую прибыль при условии : спрос на деталь А – не менее 300 шт., на деталь В – не более 200 шт.
6. При продаже двух видов товара используется 4 типа ресурсов. Норма затрат ресурсов на реализацию единицы товара, общий объем каждого ресурса заданы в таблице:
| Ресурсы | Норма затрат ресурсов на товары | Общее количество ресурсов | |
| 1-го вида | 2-го вида | ||
| 1 | 2 | 2 | 20 |
| 2 | 1 | 2 | 18 |
| 3 | 4 | 0 | 14 |
| 4 | 0 | 4 | 12 |
Прибыль от реализации одной единицы товара первого вида составляет 5 у.е., второго вида – 6 у.е.
Требуется найти оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль.
7. Для откорма крупного рогатого скота используется 2 вида кормов В1 и В2, в которые входят питательные вещества А1, А2, А3 и А4. Содержание количеств единиц питательных веществ в 1 кг каждого корма, стоимость 1 кг корма и норма содержания питательных веществ в дневном рационе животного представлены в таблице:
| Питательные вещества | Вид кормов | Норма содержания питательного вещества | |
| В1 | В2 | ||
| А1 | 3 | 4 | 24 |
| А2 | 1 | 2 | 18 |
| А3 | 4 | 0 | 20 |
| А4 | 0 | 1 | 6 |
| Стоимость 1 кг корма, у.е | 2 | 1 |
|
Составить рацион при условии минимальной стоимости.
8. Трикотажная фабрика использует для производства свитеров и кофточек чистую шерсть, силон и нитрон, запасы которых составляют, соответственно 800, 400, 300 кг. Количество трикотажного вида (кг), необходимого для изготовления 10 изделий, а также прибыль, получаемая от их реализации, приведены в таблице. Составить план производства изделий, обеспечивающий получение максимальной прибыли.
| Вид сырья | Затраты пряжи на 10 шт | |
| свитер | кофточка | |
| Шерсть | 4 | 2 |
| Силон | 2 | 1 |
| Нитрон | 1 | 1 |
| Прибыль, тыс. у.е | 6 | 5 |
9. При подкормке посевов необходимо внести на 1 га почвы не менее 8 единиц химического вещества А, не менее 21 единиц химического вещества В и не менее 16 единиц химического вещества С. Фермер закупает комбинированные удобрения двух видов 1 и 2. В таблице указаны содержание количества единиц химического вещества в 1 кг каждого вида удобрений и цена 1кг удобрений. Определить потребность фермера в удобрениях 1 и 2 вида на 1га посевной площади при минимальных затратах на их приобретение.
| Химические вещества | Содержание химических веществ в 1 кг удобрения | |
| 1 | 2 | |
| А | 1 | 5 |
| В | 12 | 3 |
| С | 4 | 4 |
| Цена 1 кг удобрения, в у.е | 5 | 2 |
10. На звероферме могут выращиваться черно-бурые лисы и песцы. Для обеспечения нормальных условий их выращивания используется 3 вида кормов. Количество корма каждого вида, которое должны получать животные, приведено в таблице. В ней также указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисы и песца.
| Вид корма | Количество единиц корма, которое ежедневно должна получать | Общее количество корма | |
| лисица | песец | ||
| I | 2 | 3 | 180 |
| II | 4 | 1 | 240 |
| III | 6 | 7 | 426 |
| Прибыль от реализации одной шкурки, в у.е | 160 | 120 |
|
Определить количество лисиц и песцов, обеспечивающий получение максимальной прибыли.
Приложение 2
Контрольные задания по теме
«Транспортные задачи»
Имеются N поставщиков и M потребителей. В таблице указаны тарифы на перевозки от поставщиков к потребителям , предложения поставщиков и спрос потребителей.
Задания:
1. Построить математическую модель транспортной задачи, заданной распределительной таблицей и решить:
1.1. методом северо-западного угла;
1.2. методом минимального элемента;
1.3. методом запрещения перевозок (см. дополнительное условие);
1.4. оптимизировать полученное решение методом потенциалов;
1.5 Проверить полученное оптимальное решение с помощью математического пакета Mathcad.
Сделать выводы.
Вариант -1
| № N/M | 1 | 2 | 3 | 4 | 5 | Предложение |
| 1 | 4 | 8 | 9 | 10 | 3 | 100 |
| 2 | 6 | 7 | 3 | 2 | 4 | 120 |
| 3 | 12 | 5 | 6 | 13 | 15 | 50 |
| 4 | 9 | 11 | 14 | 3 | 7 | 140 |
| Спрос | 70 | 130 | 40 | 50 | 140 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 2-го поставщика ко 2-му потребителю и от 3-его поставщика к 4-ому потребителю временно закрыты.
Вариант -2
| № П/П | 1 | 2 | 3 | 4 | Предложение |
| 1 | 2 | 10 | 8 | 15 | 200 |
| 2 | 4 | 2 | 3 | 6 | 170 |
| 3 | 7 | 3 | 12 | 5 | 130 |
| 4 | 12 | 10 | 4 | 8 | 90 |
| 5 | 4 | 11 | 7 | 6 | 60 |
| Спрос | 50 | 220 | 140 | 120 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 3-го поставщика ко 4-му потребителю и от 2-го поставщика к 1-ому потребителю временно закрыты.
Вариант -3
| № П/П | 1 | 2 | 3 | 4 | 5 | Предложение |
| 1 | 2 | 10 | 8 | 15 | 5 | 200 |
| 2 | 4 | 2 | 3 | 6 | 12 | 170 |
| 3 | 7 | 3 | 12 | 5 | 13 | 130 |
| 4 | 11 | 6 | 8 | 3 | 6 | 120 |
| Спрос | 50 | 220 | 140 | 120 | 70 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 4-го поставщика ко 4-му потребителю и от 2-го поставщика к 3-ему потребителю временно закрыты.
Вариант -4
| № П/П | 1 | 2 | 3 | 4 | Предложение |
| 1 | 7 | 4 | 5 | 5 | 110 |
| 2 | 9 | 6 | 12 | 8 | 130 |
| 3 | 8 | 13 | 9 | 9 | 90 |
| 4 | 10 | 2 | 3 | 11 | 80 |
| 5 | 11 | 5 | 10 | 13 | 70 |
| Спрос | 120 | 90 | 130 | 90 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 4-го поставщика ко 3-му потребителю и от 3-го поставщика к 5-ому потребителю временно закрыты.
Вариант – 5
| № П/П | 1 | 2 | 3 | 4 | 5 | Предложение |
| 1 | 3 | 10 | 8 | 7 | 5 | 200 |
| 2 | 4 | 2 | 3 | 6 | 12 | 170 |
| 3 | 7 | 3 | 10 | 5 | 13 | 130 |
| 4 | 15 | 6 | 8 | 3 | 11 | 120 |
| Спрос | 50 | 220 | 140 | 120 | 70 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 2-го поставщика ко 2-му потребителю и от 3-его поставщика к 4-ому потребителю временно закрыты.
Вариант -6
| № N/M | 1 | 2 | 3 | 4 | 5 | Предложение |
| 1 | 3 | 8 | 9 | 10 | 3 | 110 |
| 2 | 7 | 11 | 3 | 2 | 4 | 120 |
| 3 | 12 | 5 | 6 | 13 | 15 | 160 |
| 4 | 9 | 10 | 14 | 3 | 7 | 140 |
| Спрос | 70 | 130 | 40 | 50 | 150 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 4-го поставщика ко 5-му потребителю и от 2-го поставщика к 4-ому потребителю временно закрыты.
Вариант -7
| № П/П | 1 | 2 | 3 | 4 | 5 | Предложение |
| 1 | 2 | 10 | 4 | 15 | 5 | 210 |
| 2 | 4 | 2 | 3 | 6 | 12 | 170 |
| 3 | 7 | 3 | 12 | 5 | 11 | 130 |
| 4 | 11 | 6 | 8 | 8 | 14 | 140 |
| Спрос | 50 | 220 | 140 | 120 | 80 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 4-го поставщика ко 4-му потребителю и от 2-го поставщика к 3-ему потребителю временно закрыты.
Вариант -8
| № П/П | 1 | 2 | 3 | 4 | Предложение |
| 1 | 7 | 4 | 5 | 5 | 210 |
| 2 | 9 | 6 | 12 | 8 | 130 |
| 3 | 8 | 13 | 9 | 9 | 90 |
| 4 | 10 | 2 | 3 | 11 | 180 |
| 5 | 11 | 5 | 10 | 13 | 70 |
| Спрос | 120 | 150 | 130 | 190 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 1-го поставщика ко 3-му потребителю и от 3-го поставщика к 2-ому потребителю временно закрыты.
Вариант -9
| № П/П | 1 | 2 | 3 | 4 | Предложение |
| 1 | 6 | 14 | 5 | 5 | 140 |
| 2 | 9 | 6 | 2 | 8 | 150 |
| 3 | 8 | 13 | 9 | 9 | 90 |
| 4 | 10 | 2 | 3 | 12 | 120 |
| 5 | 11 | 5 | 10 | 13 | 170 |
| Спрос | 120 | 130 | 150 | 90 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 5-го поставщика ко 3-му потребителю и от 3-го поставщика к 1-ому потребителю временно закрыты.
Вариант -10
| № П/П | 1 | 2 | 3 | 4 | 5 | Предложение |
| 1 | 2 | 10 | 8 | 15 | 5 | 240 |
| 2 | 4 | 2 | 3 | 6 | 12 | 190 |
| 3 | 7 | 3 | 12 | 5 | 13 | 170 |
| 4 | 11 | 6 | 8 | 3 | 6 | 120 |
| Спрос | 150 | 120 | 230 | 120 | 70 |
|
Условие к пункту 1.3. Решить задачу при условии, если перевозки от 1-го поставщика ко 4-му потребителю и от 2-го поставщика к 5-ому потребителю временно закрыты.
Приложение 3
Контрольные задания по теме
«Задачи о назначениях»
1) Фирма, имеющая 4 склада, получила 4 заказа, которые необходимо доставить различным потребителям. Складские помещения каждой базы имеют вполне достаточное количество товара, чтобы выполнить любой один из этих заказов. Расстояния между каждой базой и каждым потребителем приведены в матрице

Как следует распределить заказы по базам, чтобы общая дальность была минимальной?
2) Фирма объединяет 3 предприятия, каждое из которых производит 3 вида изделий.
Себестоимости каждого изделия в усл. ед. при изготовлении на каждом предприятии указаны в матрице
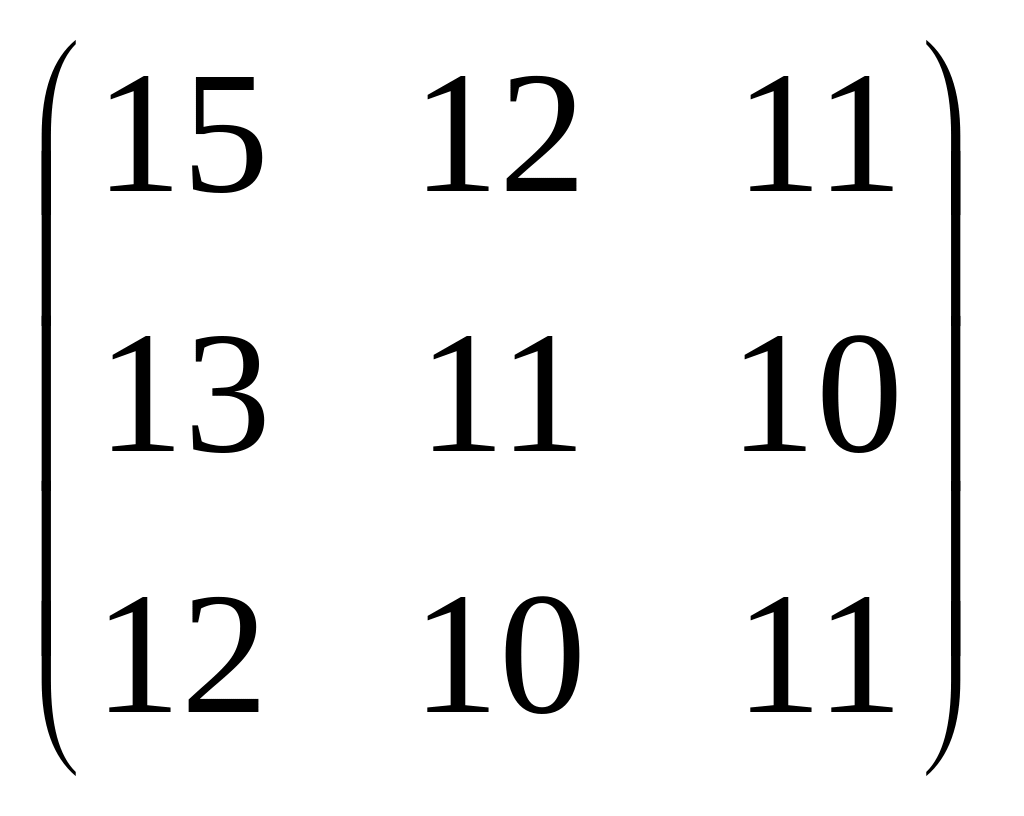
Учитывая необходимость специализации каждого предприятия только по одному изделию, распределить производство изделий по предприятиям так, чтобы изделия имели минимальную себестоимость.
3) Фирма имеет три механизма ![]() , каждый из которых может быть использован на каждом из трех видов работ
, каждый из которых может быть использован на каждом из трех видов работ ![]() , с производительностью, заданной матрицей (в условных единицах)
, с производительностью, заданной матрицей (в условных единицах)
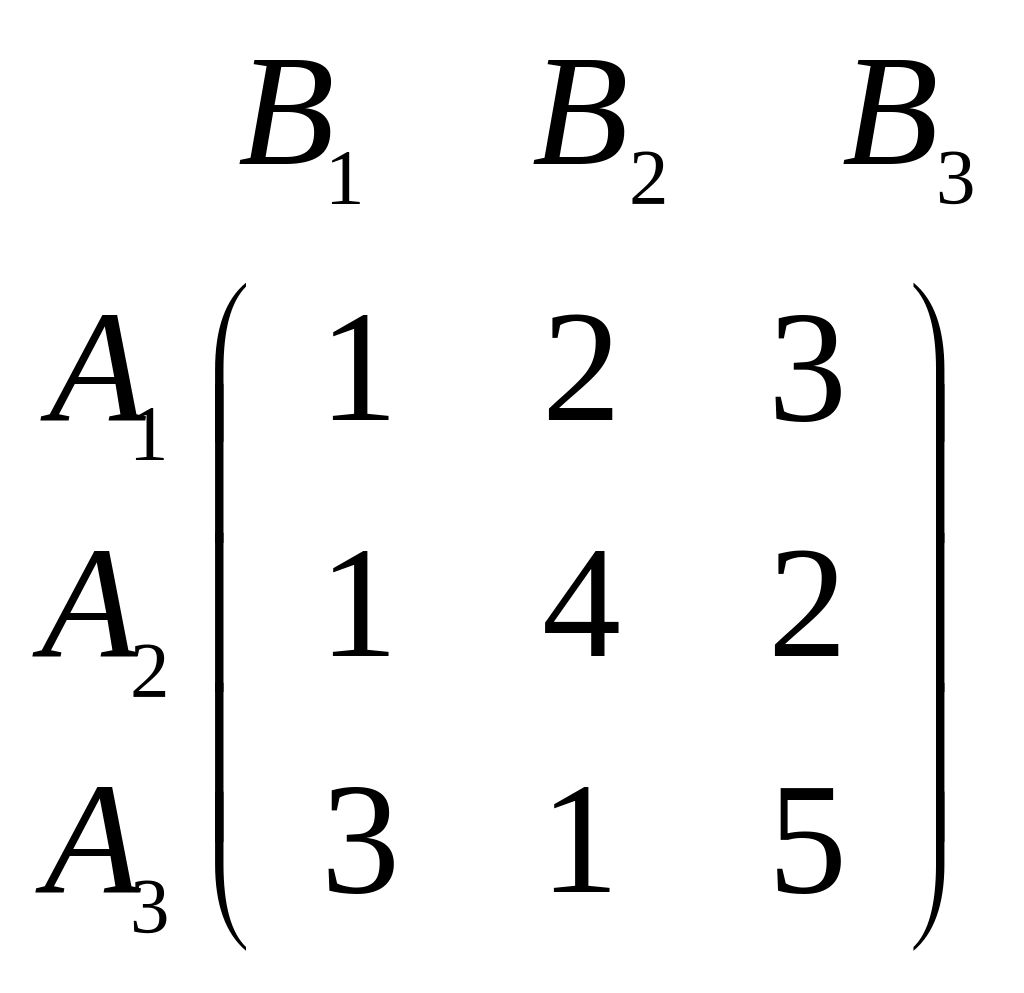
Распределить механизмы по одному на каждую из работ так, чтобы суммарная производительность всех механизмов была максимальной.
4) Фирма имеет 5 механизмов, каждый из которых может быть использован на каждом из 4-ех видов работ, с производительностью, заданной матрицей (в условных единицах)
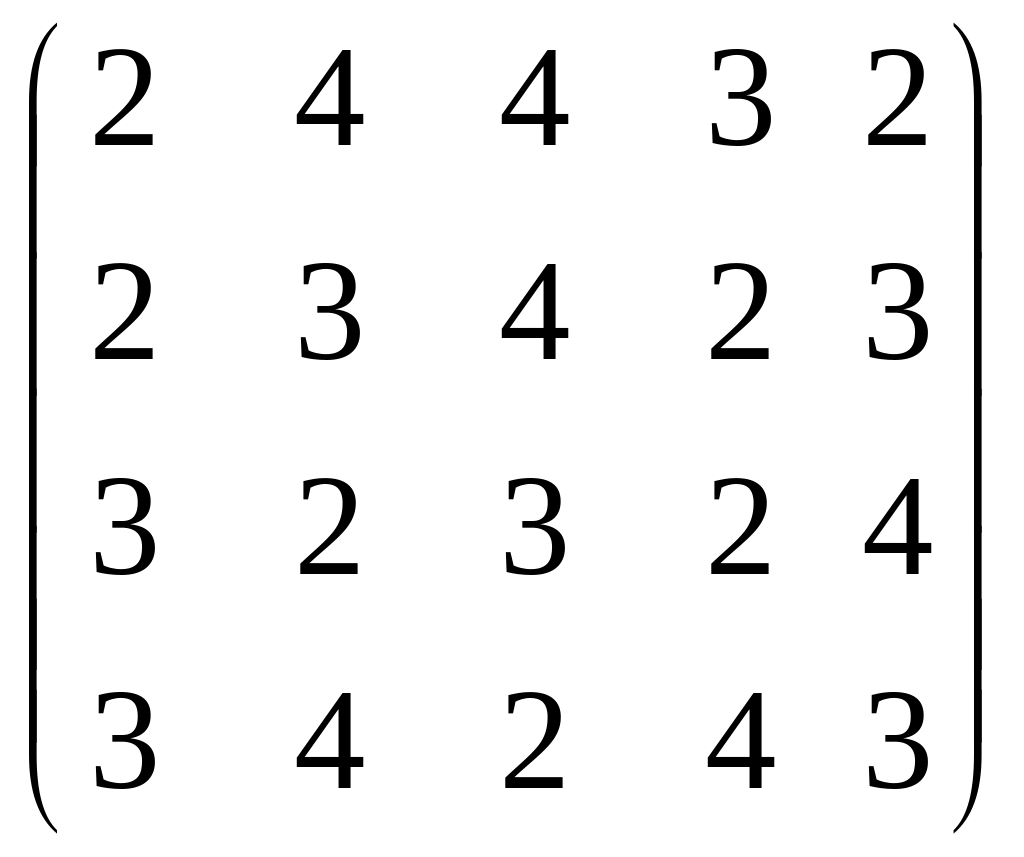
Распределить механизмы по одному на каждую из работ так, чтобы суммарная производительность всех механизмов была максимальной.
5) Пять человек должны выполнить четыре работы, причем каждый из работников с разной производительностью может выполнить любую из этих работ. Предусматривается, что каждый работник в состоянии сделать только одну работу.
Производительности работников при выполнении работ заданы матрицей:
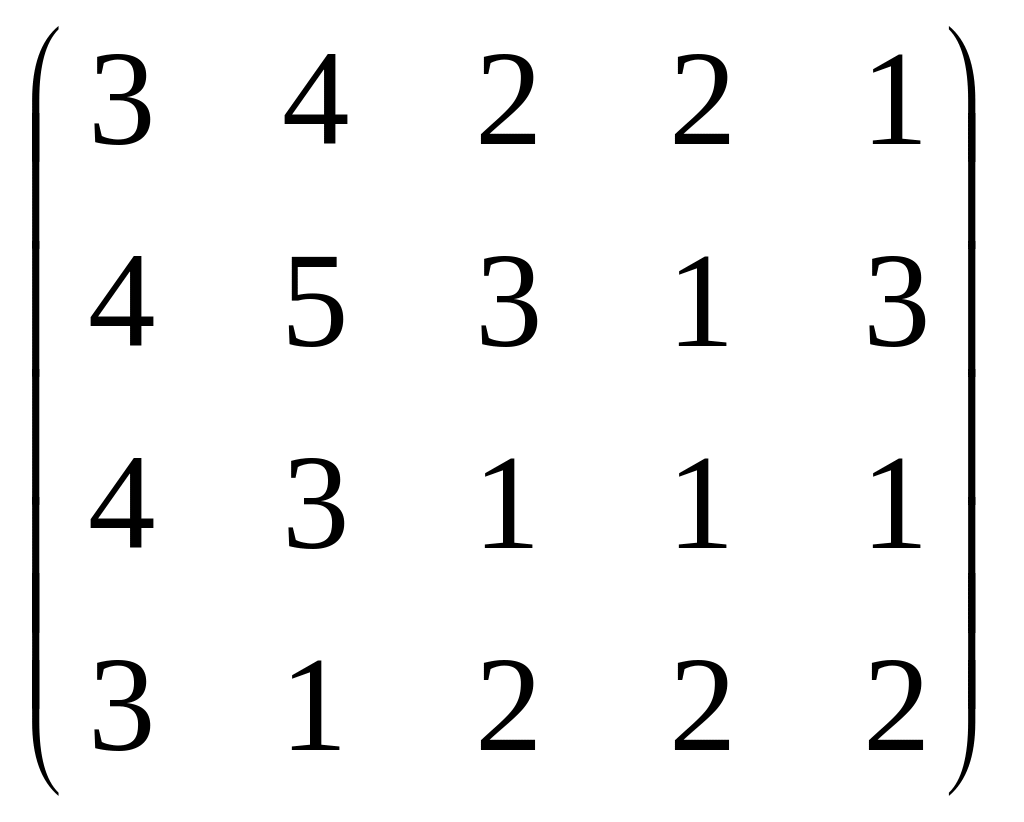
Распределить людей на работу так, чтобы выполнить ее с максимальной производительностью.
6) Институт получил гранты на выполнение четырех исследовательских проектов. Выходные результаты первого проекта являются входными данными для второго проекта, выходные результаты второго проекта – это входные данные для третьего проекта, результаты третьего проекта используются для работы над четвертым проектом. В качестве научных руководителей проектов рассматриваются кандидатуры четырех ученых, обладающих различным опытом и способностями. Каждый ученый оценил время, необходимое ему для реализации проекта.
Матрица времен имеет вид:
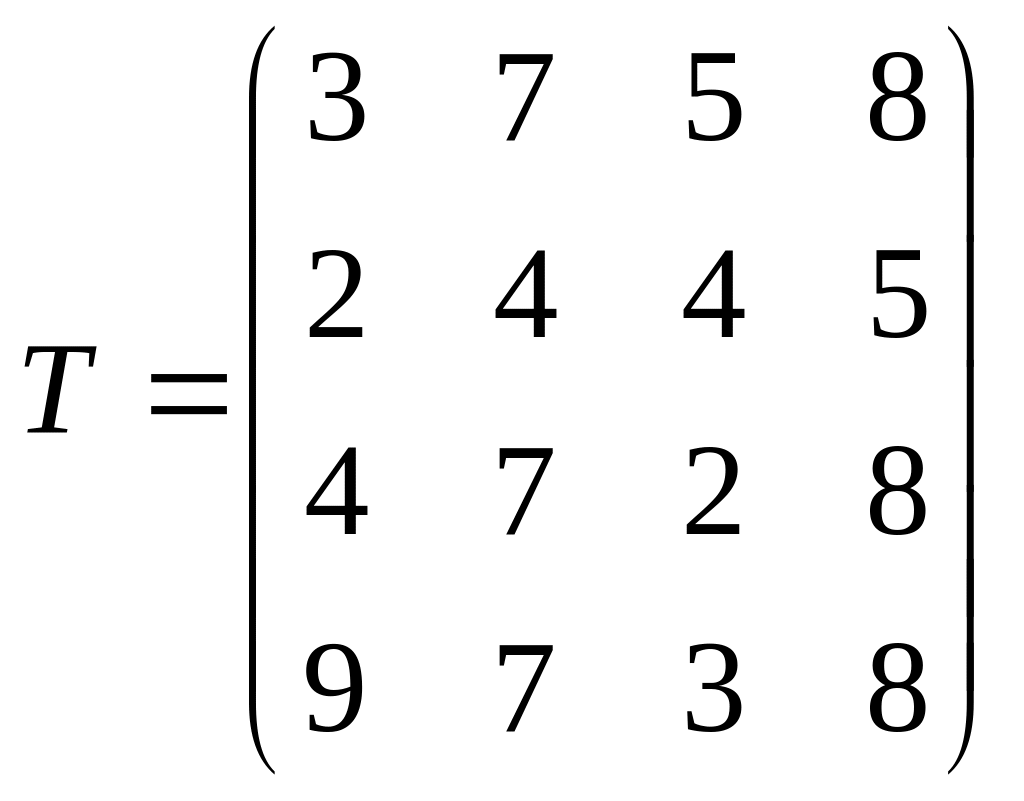
![]()
Продолжительность времени задана в месяцах. Требуется выбрать научного руководителя для выполнения каждого проекта так, чтобы суммарное время выполнения всех проектов было минимальным.
7) На предприятии имеются 5 станков различных видов, каждый из которых может выполнять пять различных операции по обработке деталей. Известна производительность каждого станка при выполнении каждой операции, заданная матрицей:
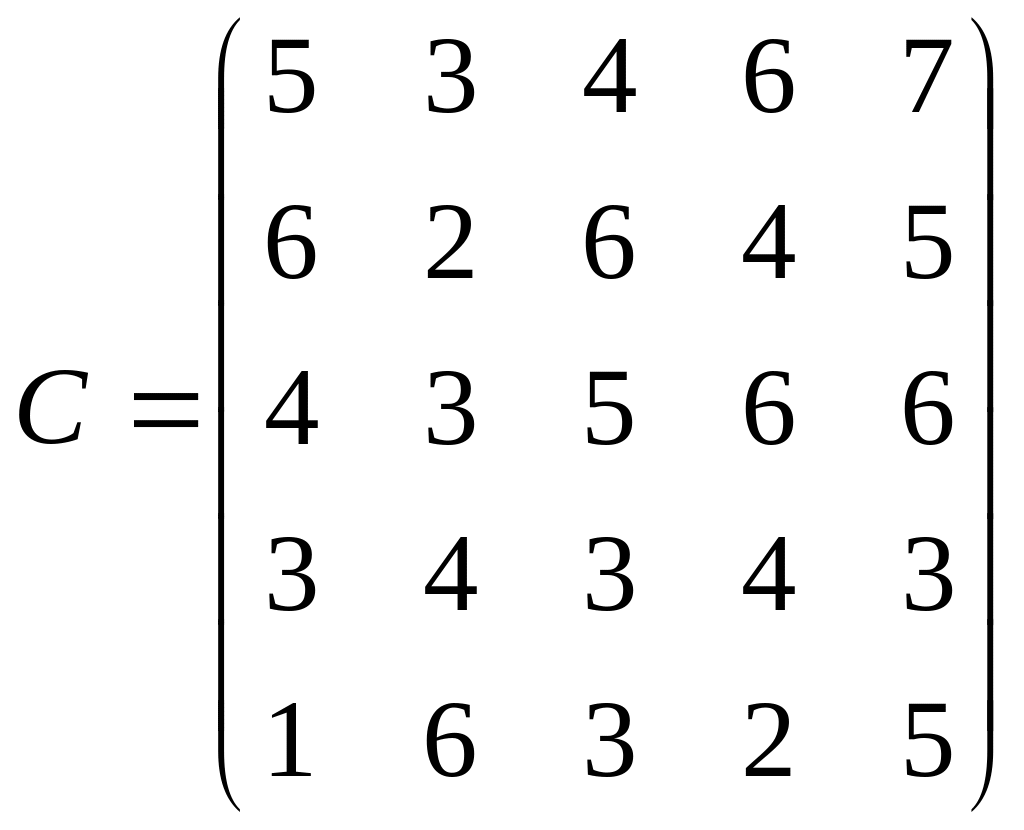
Определить какую операцию и за каким станком, нужно закрепить, чтобы суммарная производительность была максимальной при условии, что за каждым станком закреплена только одна операция.
8) На предприятии имеются 4 станка различных видов, каждый из которых может выполнять пять различных операции по обработке деталей. Известна производительность каждого станка при выполнении каждой операции, заданная матрицей:
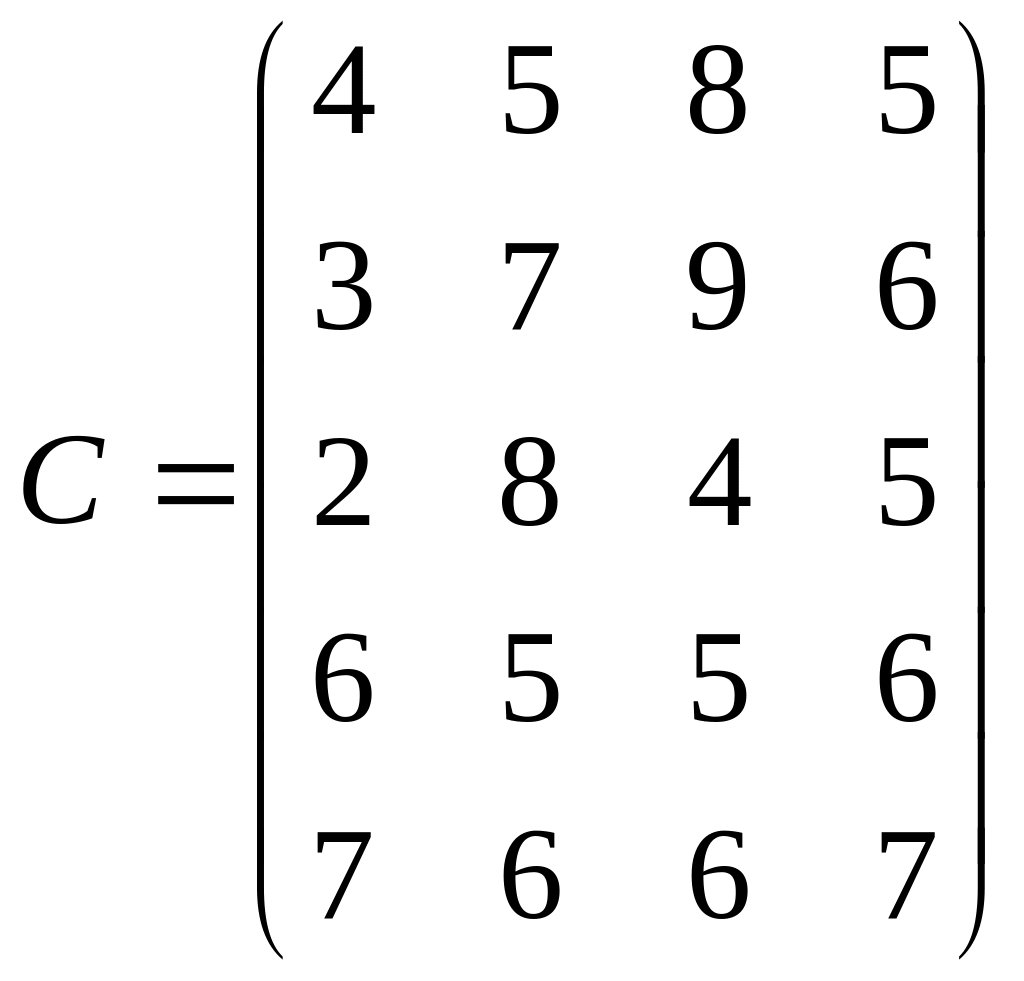
Определить какую операцию и за каким станком, нужно закрепить, чтобы суммарная производительность была максимальной при условии, что за каждым станком закреплена только одна операция.
9) Торговая фирма продает товары в 4-ех различных городах. Для реализации товаров фирма располагает 4-мя торговыми агентами. Величина покупательных способностей, реализуемых каждым из агентов в каждом городе характеризируется матрицей: 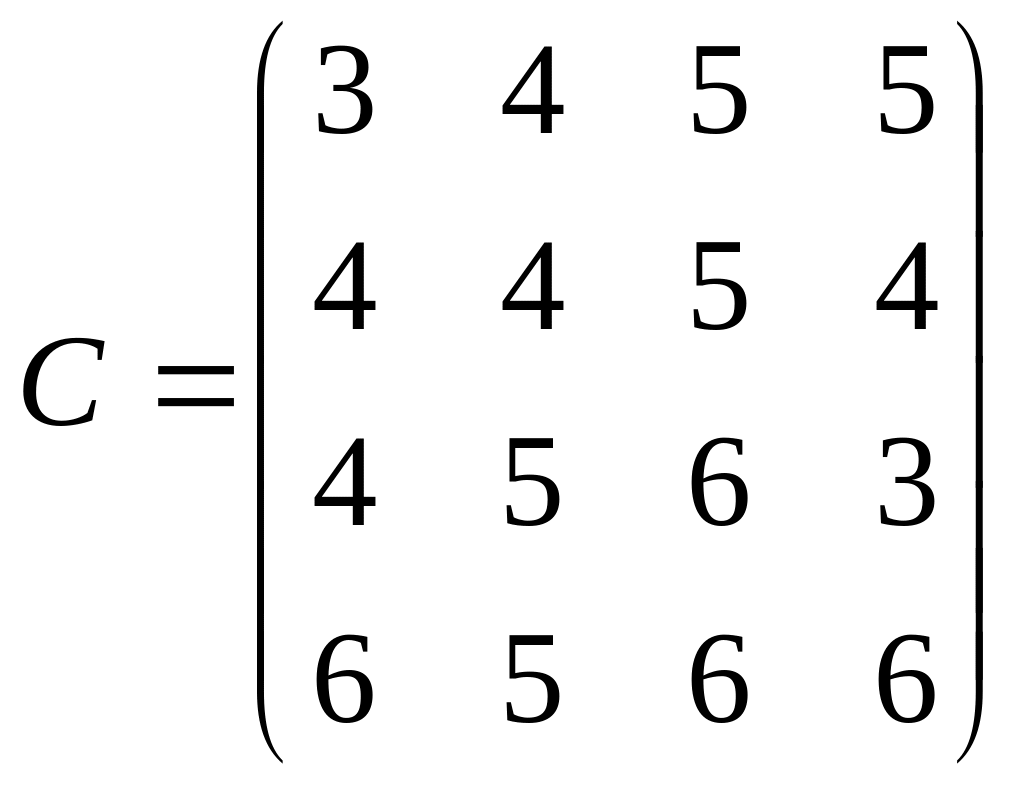 . Как следует распределить агентов по городам, чтобы фирма получила максимальную прибыль?
. Как следует распределить агентов по городам, чтобы фирма получила максимальную прибыль?
10) Группе, исследующей рынок, требуется получить данные из 5-ти различных мест. В ее распоряжении имеется 5 дней, и она предполагает провести по одному дню в каждом месте, проведя по 7 опросов (j=1,…,7). Величина матрицы Рij, показывает число успешных опросов в j-ом месте в течении i-го дня. (i=1,…,5)
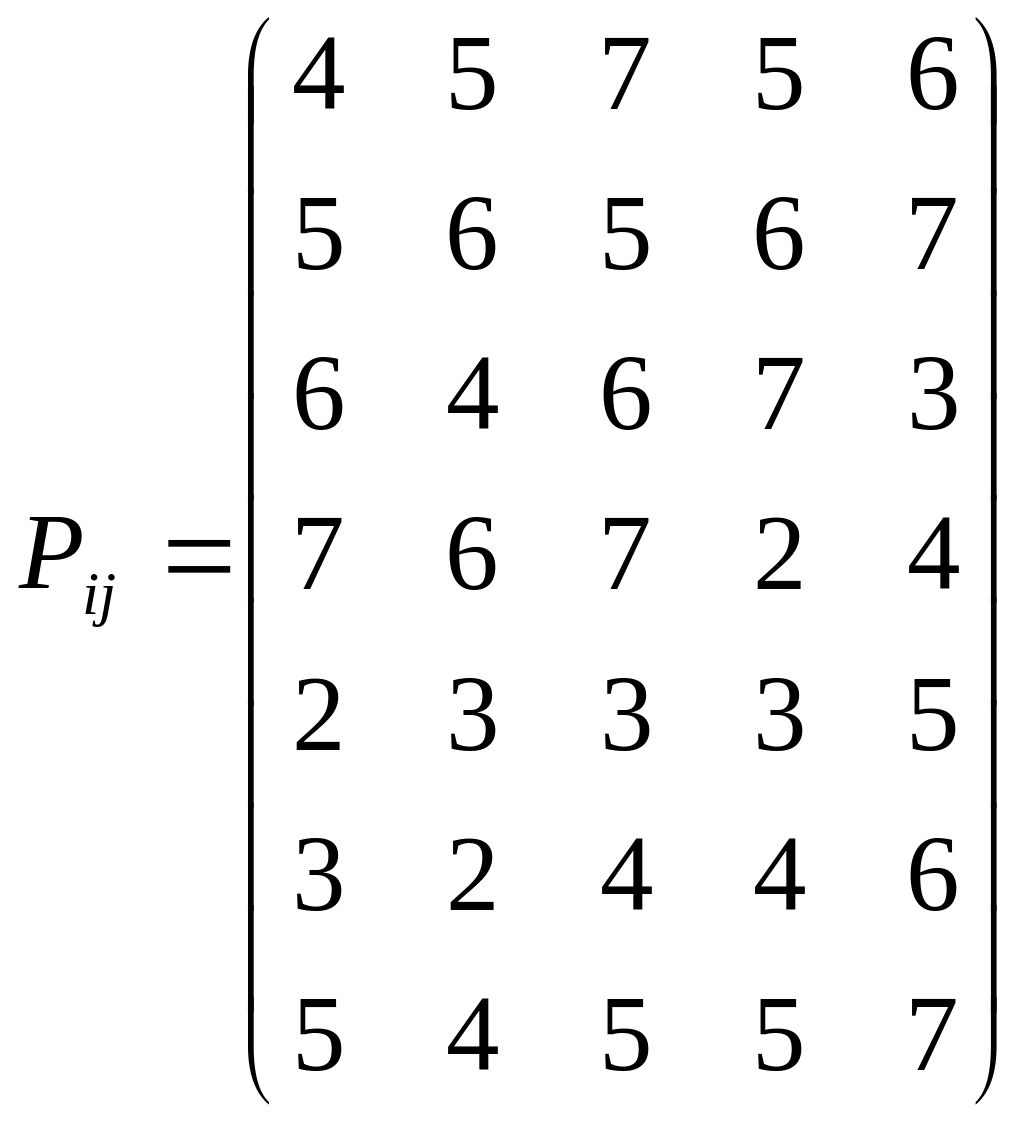 . Определить время проведения опросов, при котором общее число опросов максимально.
. Определить время проведения опросов, при котором общее число опросов максимально.
Приложение 4
Контрольные задания по теме
«Симплекс – метод»
Предприятие рекламирует свою продукцию с использованием 4-ех источников массовой информации: телевидения, радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом показал, что эти средства приводят к увеличению прибыли соответственно на a, b, c и d у .е. в расчете на 1 у.е., затраченную на рекламу. На рекламу выделено N у.е. Администрация предприятия не намерена тратить на телевидение более 40%, а на радио и газеты – не более 50% общей суммы выделенных средств. Как следует предприятию организовать рекламу, чтобы получить максимальную прибыль?
| № варианта | a | b | c | d | N |
| 1 | 10 | 5 | 7 | 4 | 50000 |
| 2 | 10 | 6 | 7 | 4 | 50000 |
| 3 | 10 | 5 | 6 | 3 | 60000 |
| 4 | 9 | 6 | 7 | 4 | 60000 |
| 5 | 9 | 6 | 5 | 4 | 48000 |
| 6 | 9 | 7 | 6 | 5 | 48000 |
| 7 | 9 | 6 | 5 | 4 | 52000 |
| 8 | 10 | 6 | 5 | 3 | 52000 |
| 9 | 10 | 5 | 6 | 3 | 54000 |
| 10 | 10 | 6 | 5 | 4 | 54000 |
Приложение 5
Вопросы к зачету
Модель. Математическая и экономико-математическая модели.
Классификация моделей и их характеристика.
Основные принципы построения моделей.
Общая постановка задачи линейного программирования. План, допустимый план, оптимальное решение задачи ЛП .
Алгоритм решения задач линейного программирования графическим методом.
Общая постановка транспортной задачи.
Открытая и закрытая транспортные задачи. Приведение открытой транспортной задачи к закрытой.
Получение начального плана перевозок транспортной задачи.
Оптимизация начального плана транспортной задачи. Метод потенциалов.
Вырожденный и невырожденный план транспортной задачи. Способы исключения вырожденности.
Приложения транспортных моделей.
Общая постановка задачи о назначениях.
Алгоритм решения задач о назначениях (венгерский метод).
Симплекс – метод. Алгоритм решения задач линейного программирования симплекс – методом.
Литература
И.Л. Акулич. Математическое программирование в примерах и задачах. Издательство «Высшая школа» Москва, 1986.
Е.К.Хеннер, А.П.Шестаков. Математическое моделирование: Пособие для учителя. Пермь, 1995.
В.И. Малыхин. Математическое моделирование экономики. Издательство УРАО Москва, 1998.
М.С. Красс, Б.П.Чупрынов. Основы математики и ее приложения в экономическом образовании. Издательство «Дело», Москва, 2000.
П.В. Конюховский. Математические методы исследования операций в экономике. Издательство «Питер», Санкт – Петербург, 2000.
О.О.Замков, А.В. Толстопятенко, Ю.Н. Черемных. Математические методы в экономике. Издательство «Дело и сервис», Москва, 2001.
Л.Э. Хазанова. Математические методы в экономике. Издательство «БЕК», Москва, 2002.
Л.Я. Разживина, И.В. Шаркевич. Решение транспортной задачи средствами MatCAD. журнал «Информатика и образование», №5, 2004.
Г.И. Просветов. Математика в экономике: Задачи и решения: Учебно-методическое пособие. – М.: Издательство РДЛ, 2004.
Г.И. Просветов. Математические методы в экономике. : Учебно-методическое пособие. – М.: Издательство РДЛ, 2004.
Похожие файлы
object(ArrayObject)#853 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(100) "Робототехника: конструирование и программирование Lego "
["seo_title"] => string(58) "robototiekhnika-konstruirovaniie-i-proghrammirovaniie-lego"
["file_id"] => string(6) "126587"
["category_seo"] => string(7) "prochee"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1415199008"
}
}
object(ArrayObject)#875 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(179) "Педагогический проект "Решение экономических задач с использованием информационных технологий" "
["seo_title"] => string(112) "piedaghoghichieskii-proiekt-rieshieniie-ekonomichieskikh-zadach-s-ispol-zovaniiem-informatsionnykh-tiekhnologhii"
["file_id"] => string(6) "172959"
["category_seo"] => string(11) "informatika"
["subcategory_seo"] => string(7) "prochee"
["date"] => string(10) "1423906724"
}
}
object(ArrayObject)#853 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(83) "Брейн-ринг "Длина окружности и площадь круга" "
["seo_title"] => string(49) "briein-ringh-dlina-okruzhnosti-i-ploshchad-krugha"
["file_id"] => string(6) "203490"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(11) "presentacii"
["date"] => string(10) "1429506592"
}
}
object(ArrayObject)#875 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(73) "Алгоритм и его практическое применение "
["seo_title"] => string(47) "alghoritm-i-iegho-praktichieskoie-primienieniie"
["file_id"] => string(6) "161279"
["category_seo"] => string(11) "informatika"
["subcategory_seo"] => string(5) "uroki"
["date"] => string(10) "1422198517"
}
}
object(ArrayObject)#853 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(181) "Эффективные алгоритмы численного решения уравнений, систем, расчета производных, интегралов в Scilab"
["seo_title"] => string(114) "effiektivnyie-alghoritmy-chisliennogho-rieshieniia-uravnienii-sistiem-raschieta-proizvodnykh-intieghralov-v-scilab"
["file_id"] => string(6) "264211"
["category_seo"] => string(11) "informatika"
["subcategory_seo"] => string(11) "presentacii"
["date"] => string(10) "1449671339"
}
}
Подтверждение авторства
Пожалуйста, введите ваш Email.
Если вы хотите увидеть все свои работы, то вам необходимо войти или зарегистрироваться
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт



















