| Целеполагание и мотивация | Обеспечение мотивации учения детьми, принятия ими целей урока | Проблемная ситуация - Какое выражение не подходит под правило делимости произведения? Почему?
Цель урока - Сформулируйте тему нашего урока. Чему мы должны научиться на уроке?
- Запишем число и тему нашего урока в тетрадях (слайд)
| В последнем выражении представлена сумма
Тема: Делимость суммы и разности выражений. Цель нашего урока: Вывести признаки делимости суммы и рахности выражений Рассмотреть, где можно их применять
Делимость суммы и разности выражений. |
|
| Усвоение новых знаний и способов усвоения | Обеспечение восприятия, осмысления и первичного запоминания детьми изучаемой темы: делимость суммы и разности чисел |
- Работа с учебником. Устно: № 768 – 771 (слайд)
– Верно ли утверждение:(слайд) (а) Если хотя бы одно слагаемое делится на некоторое число, то и сумма делится на это число ( если нет, привести контрпример) б) Если ни одно из слагаемых не делится на некоторое число, то и сумма не делится на это число
в) Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число
– Сформулируйте свойство делимости суммы чисел. Если а 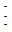 b и c b и c 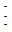 b, то (a + c) b, то (a + c) 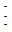 b. b.
Если а 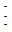 b и c не делится на b, то (a + c) не делится на b. b и c не делится на b, то (a + c) не делится на b. - Сформулируйте словами и приведите пример
Если а 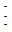 b и (a + c) b и (a + c) 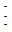 b, то ? b, то ? - Пример Если а 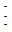 b и b b и b 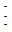 c, то ? c, то ? - Пример
| |
|
|
- утверждение неверное, контрпример: (24 + 25) не делится на 2; - утверждение не всегда верное, например, в сумме (15 + 17) ни одно из слагаемых не делится на 2, а сумма делится на 2; в сумме (14+17) ни одно из слагаемых не делится на 3 и сумма 31 не делится на 3.
- да, это утверждение всегда верное.
-если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число
- Если каждое слагаемое, кроме одного делится на некоторое число, то сумма не делится на это число - c 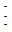 b. b.
- a 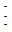 с. с. |
|
| Организация первичного закрепления | Установление правильности и осознанности изучения темы «Делимость суммы и разности чисел ». Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для диктанта по новому материалу. | Работа в парах - Решите устно № 776, 777, 778, 779. Ответьте на вопросы задач, не выполняя вычислений. Укажите, какие свойства делимости вы при этом используете?
- Письменно № 780а
– Подумайте, можно правило делимости суммы распространить и на разность? – Сформулируйте свойство делимости разности чисел.
Математический диктант.(слайд) а) (75 + 38) 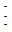 5 (нет) 5 (нет) б) (27 – 45) 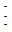 3 (да) 3 (да) в) (72 + 36 + 24) 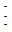 9 (нет) 9 (нет) г) (25 + 35) 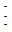 10 (да) 10 (да) д) (48 – 34 + 62) 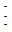 2 (да) 2 (да) е) (77 + 33) 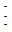 11 (да) 11 (да)
Физкультминутка Мы все вместе улыбнемся, Подмигнем слегка друг другу, Вправо, влево повернемся И кивнем затем по кругу. Все идеи победили, Вверх взметнулись наши руки. Груз забот с себя стряхнули И продолжим путь науки
№ 781 (а, в) (на доске и в тетради).
№ 799 (а, б) (с проверкой) – самостоятельно.
|
(№ 776: можно расставить на три полки, так как и 27, и 18 делятся на 3, значит, сумма также делится на 3. № 777: нельзя, так как 51 на 2 не делится. № 778: можно, так как все эти числа делятся на 4. № 779: нельзя, так как 48 на 5 не делится.)
Проверяем через документ - камеру
- можно, т.к. разность можно всегда заменить суммой
если уменьшаемое и вычитаемое делится на некоторое число, то и разность делится на это число
Решение: а) 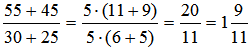 ; ; 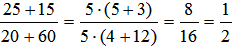 ; ; в) 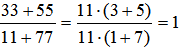 ; ; 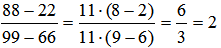 . .
|
|
| Подведение итогов урока Рефлексия | Дать качественную оценку работы класса и отдельных обучаемых Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации, их собственной деятельности и взаимодействия с учителем и другими детьми в классе | – Над какой темой работали? – Какие задания выполняли? Какие из них вызвали затруднения? Почему? – Оцените свою работу на уроке. 1 -Урок полезен, все понятно. 2 – Лишь кое –что чуть – чуть неясно. 3 – Еще придется потрудиться. 4 - Да. Трудно все – таки учиться!
|
на цветке ставят оценку |
|
















