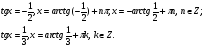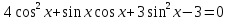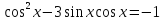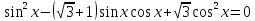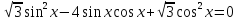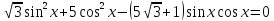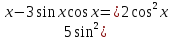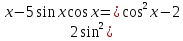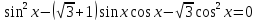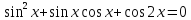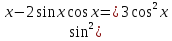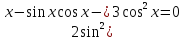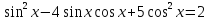10 сыныпта алгебра курсындағы тригонометриялық теңдеулерді шешу дағдыларын жетілдіру.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Біртекті тригонометриялық теңдеулерді шешу
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Біртекті тригонометриялық теңдеулерді шешу»
Полезное для учителя
Распродажа видеоуроков!
1910 руб.
3190 руб.
1690 руб.
2820 руб.
1900 руб.
3170 руб.
1730 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
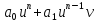 +
+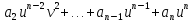
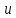 және
және 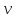 ға байланысты
ға байланысты 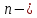 дәрежелі біртектес теңдеу деп аталады.
дәрежелі біртектес теңдеу деп аталады.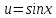 және
және 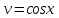 болса, онда жоғарыдағы формула біртектес тригонометриялық теңдеу деп аталады.
болса, онда жоғарыдағы формула біртектес тригонометриялық теңдеу деп аталады.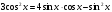 теңдеуін шешіңдер.
теңдеуін шешіңдер.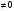 деп алып, теңдеудің екі жағын да cos
деп алып, теңдеудің екі жағын да cos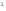 x-қа бөлеміз.
x-қа бөлеміз. 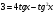 немесе
немесе 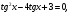 яғни tgx-ке қатысты квадрат теңдеуді аламыз. tg-ті a арқылы белгілесек,
яғни tgx-ке қатысты квадрат теңдеуді аламыз. tg-ті a арқылы белгілесек, 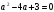 квадрат теңдеуі шығады.
квадрат теңдеуі шығады. 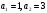 түбірлерін табамыз.
түбірлерін табамыз.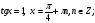
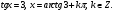
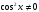 шарты қойылғанда берілген теңдеудің шешімдері жоғалуы мүмкін, болғандықтан cosx=0 теңдеуін шешіп, оның шешімдері берілген теңдеудің шешімі бола ма, соны тексеру қажет.
шарты қойылғанда берілген теңдеудің шешімдері жоғалуы мүмкін, болғандықтан cosx=0 теңдеуін шешіп, оның шешімдері берілген теңдеудің шешімі бола ма, соны тексеру қажет.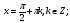 шығады.
шығады. 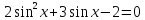 теңдеуін шешейік.
теңдеуін шешейік.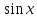 функциясына қатысты квадрат теңдеу болып табылады. Егер
функциясына қатысты квадрат теңдеу болып табылады. Егер 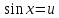 алмастыруын жасасақ, онда
алмастыруын жасасақ, онда 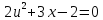 түріндегі алгебралық квадрат теңдеу аламыз, оның түбірлері
түріндегі алгебралық квадрат теңдеу аламыз, оның түбірлері 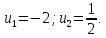
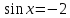 және
және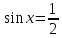 түріндегі қарапайым екі теңдеуге келеді.
түріндегі қарапайым екі теңдеуге келеді.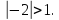
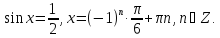 Енді табылған түбірдің берілген теңдеуді қанағаттандыратынын тексерейік.
Енді табылған түбірдің берілген теңдеуді қанағаттандыратынын тексерейік. 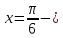 ны берілген теңдеуге қоямыз. Сонда
ны берілген теңдеуге қоямыз. Сонда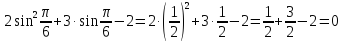 .
. 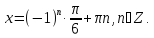
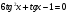 теңдеуін шешіңдер.
теңдеуін шешіңдер.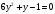 теңдеуін шешеміз. Сонда
теңдеуін шешеміз. Сонда 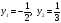 .
.