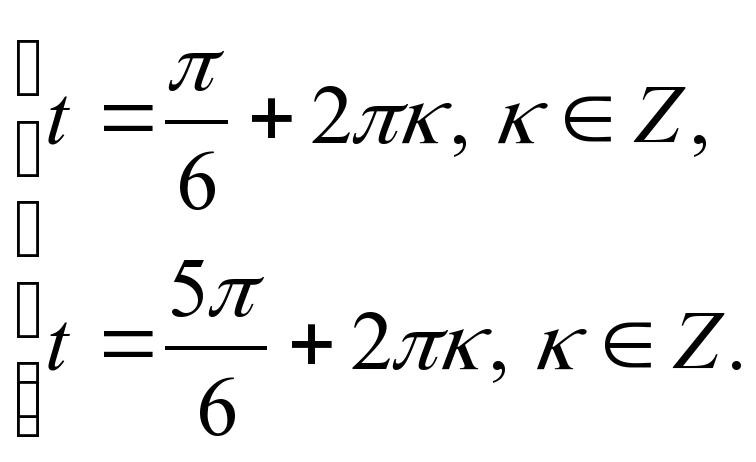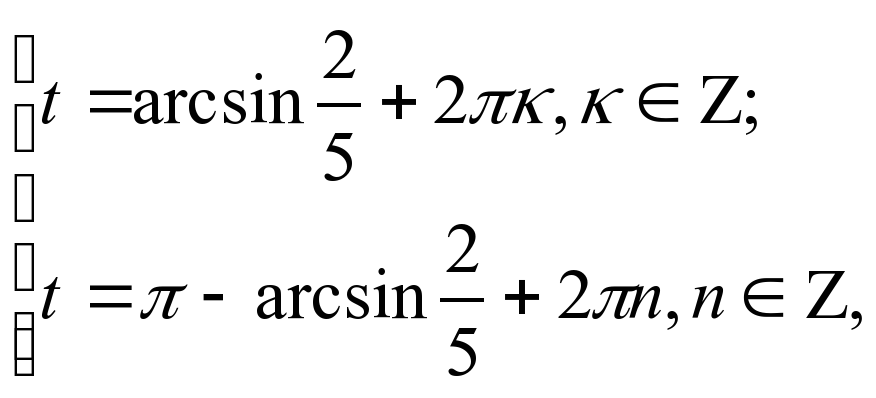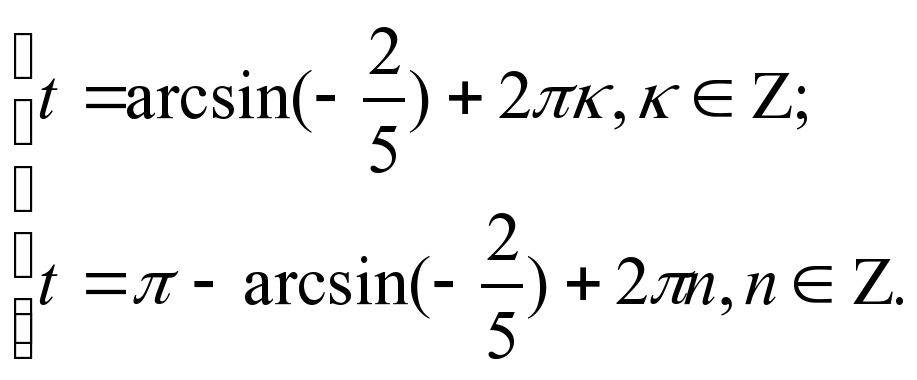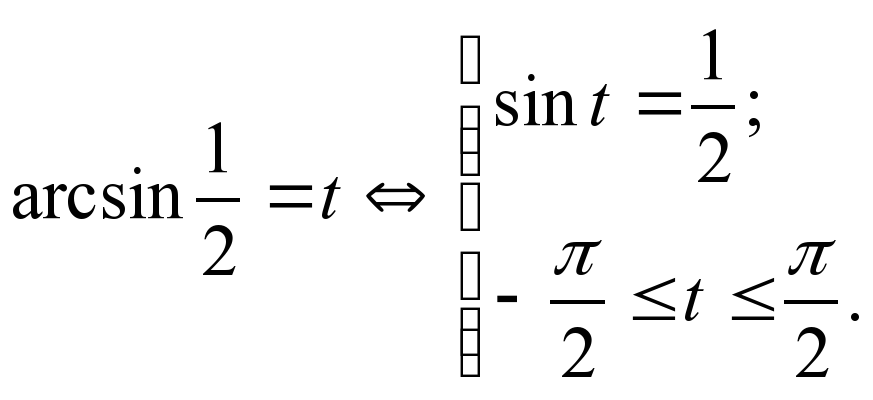| V | Изучение нового материала. Ввести проблемную ситуацию: любое ли тригонометрическое уравнение вида sint = a можно решить с помощью числовой окружности? 1) Предложить учащимся решить уравнение sin t = 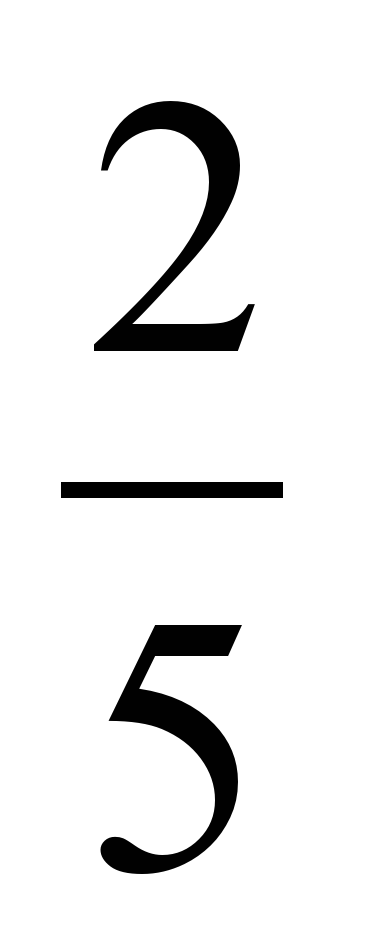 . . С помощью числовой окружности получим t1 и t2. Когда впервые возникла ситуация с решение уравнений такого типа, ученым-математикам пришлось придумать способ её описания на математическом языке. В рассмотрение был введен новый символ arcsin а. Читается: арксинус а; «arcus» в переводе с латинского значит «дуга» (сравните со словом «арка»). С помощью этого символа числа t1 и t2 записываются следующим образом: t1 = arcsin 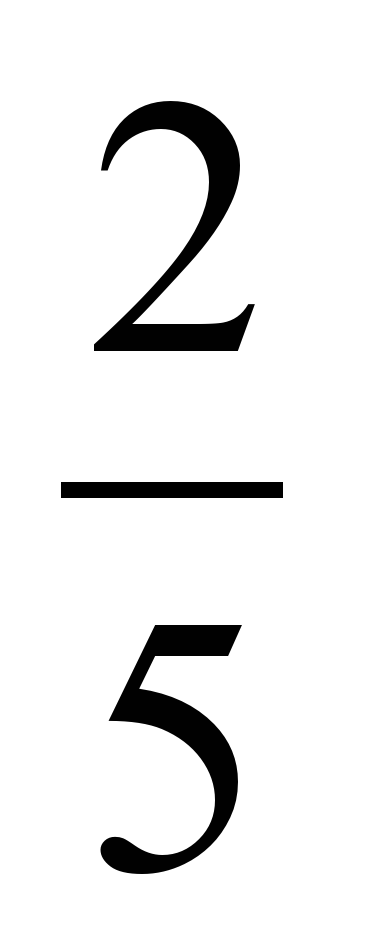 , t2 = � , t2 = �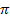 �– arcsin �– arcsin 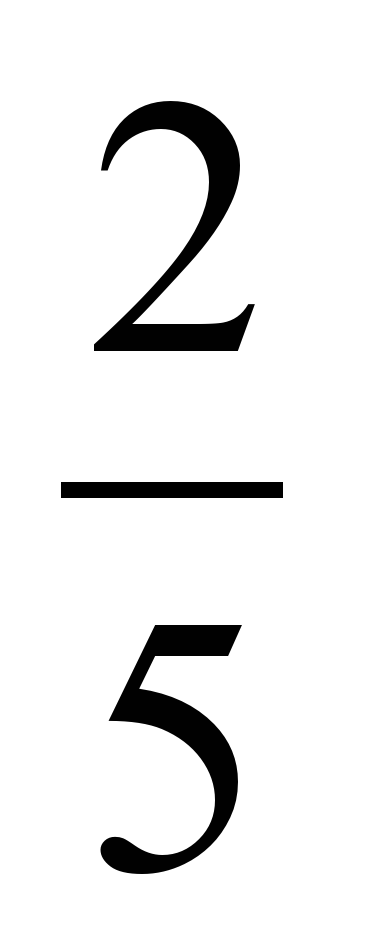 . . Теперь с помощью этого символа корни уравнения sin t = 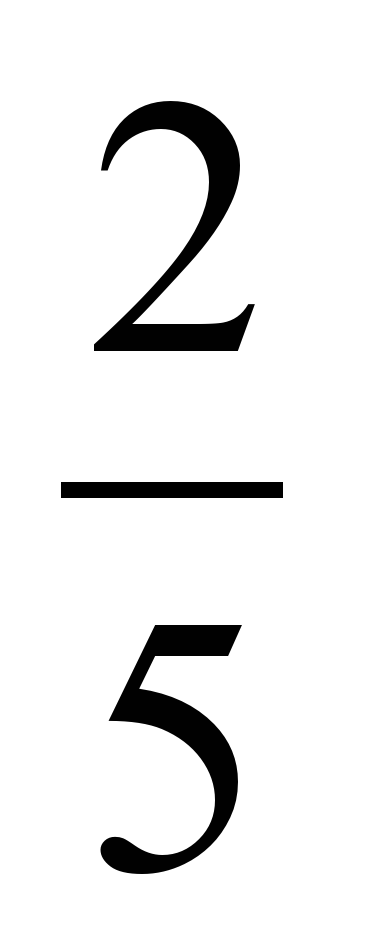 можно записать так: можно записать так: 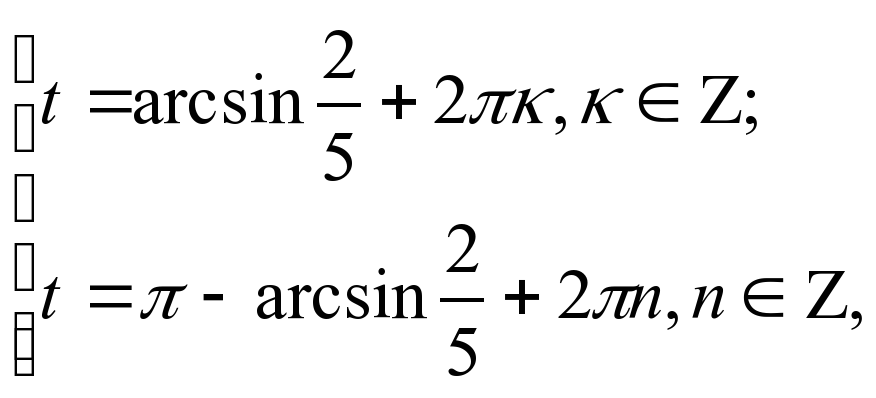 Предложить учащимся обобщить полученные знания, ответив на вопрос: «Что же означает arcsin 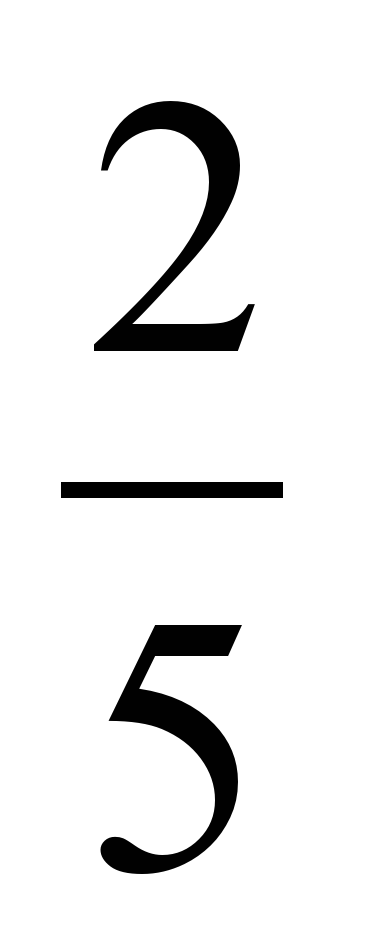 ?» ?» Вывод: это число (длина дуги), синус которого равен 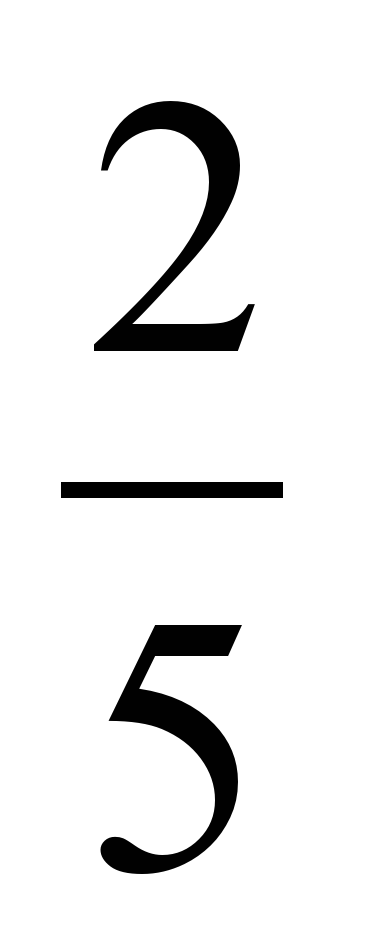 и которое принадлежит первой четверти числовой окружности. и которое принадлежит первой четверти числовой окружности. 2) Решить уравнение sin t = – 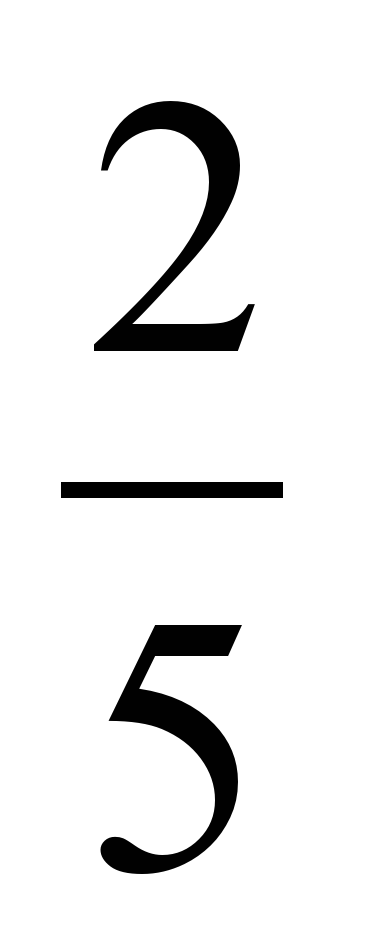 . . С помощью числовой окружности и символа arcsin а получим: 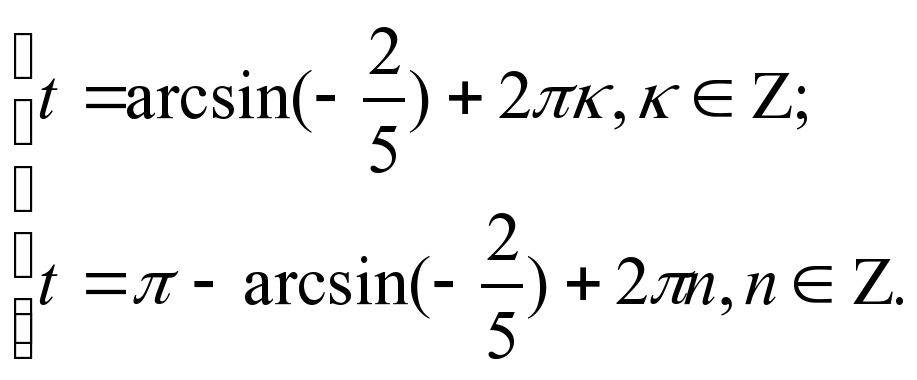
Предложить учащимся обобщить полученные знания, ответив на вопрос: «Что же означает arcsin (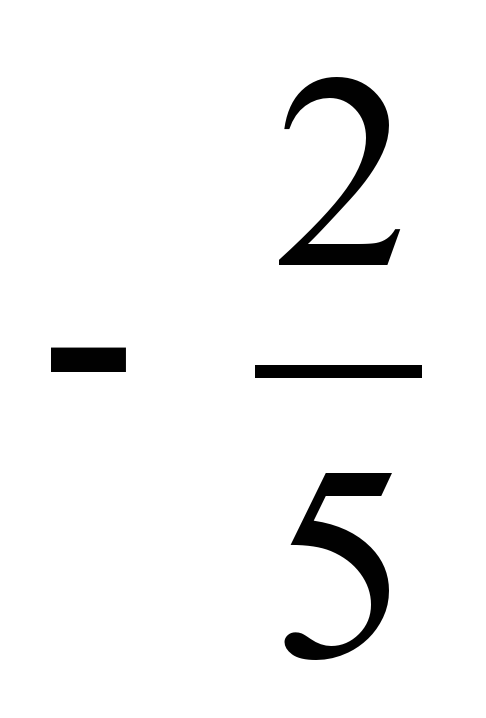 ) ?» ) ?» Вывод: это число (длина дуги), синус которого равен 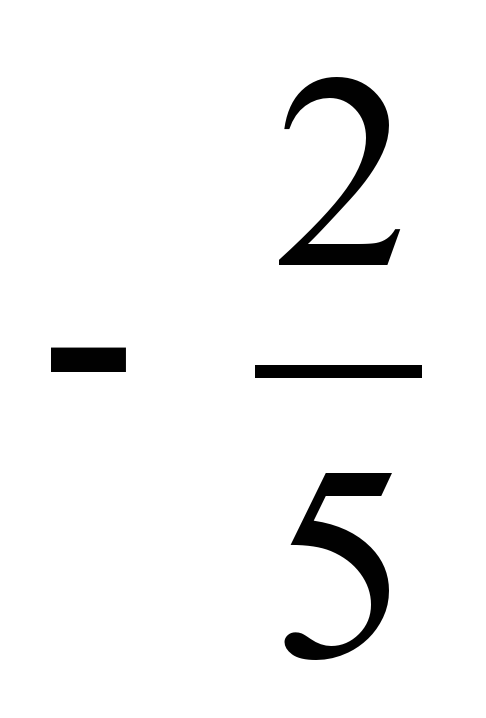 и которое принадлежит четвёртой четверти числовой окружности. и которое принадлежит четвёртой четверти числовой окружности.
3) Сформулировать определение арксинуса в общем виде.
4) Рассмотреть примеры на вычисление арксинуса. Пример 1. Вычислите arcsin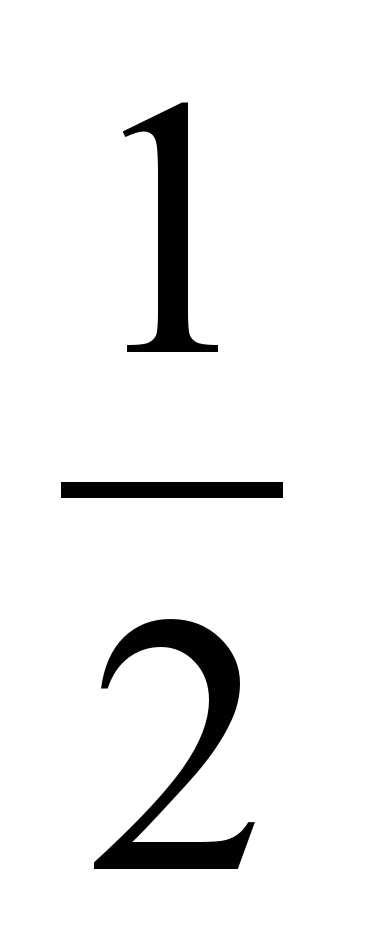 . . Решение. Пусть 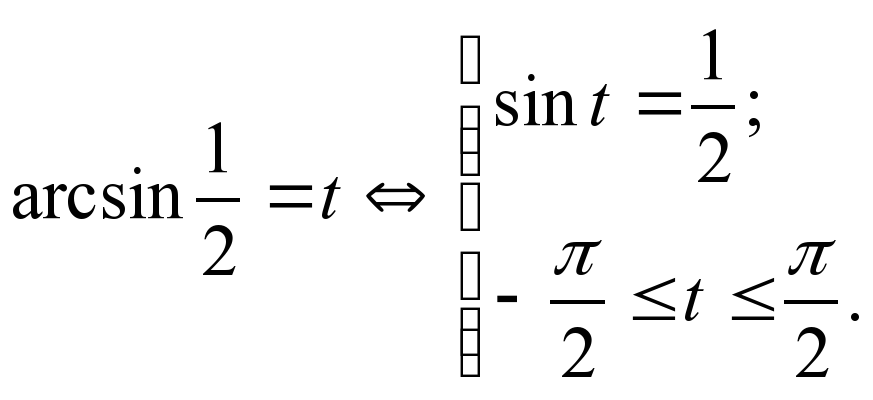 Значит, 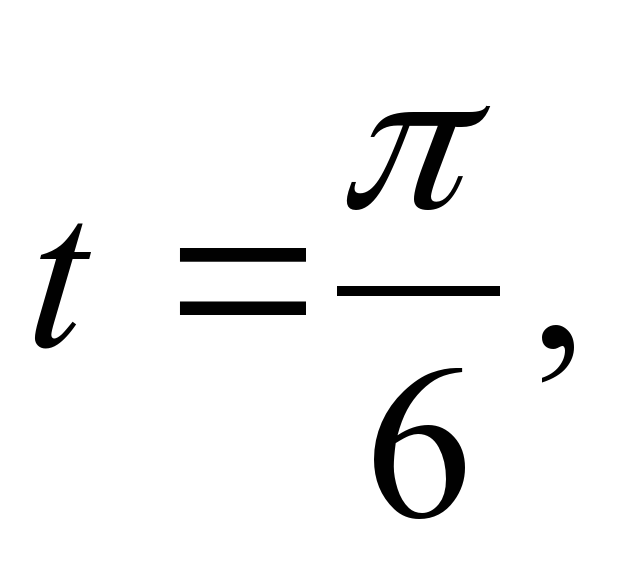 поскольку поскольку 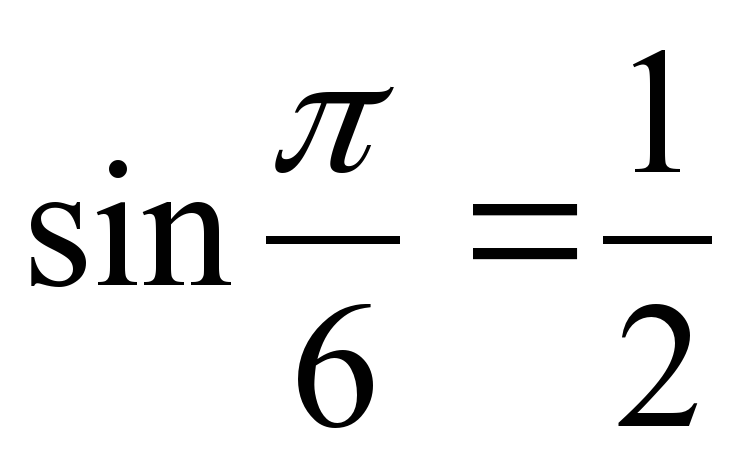 и и 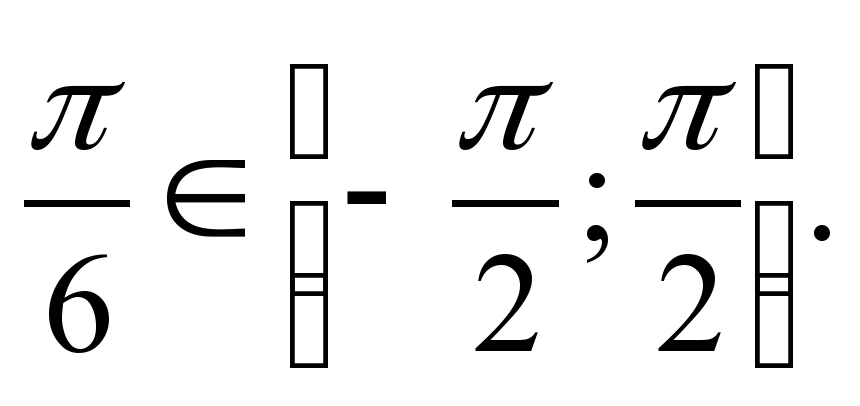 Итак, arcsin Итак, arcsin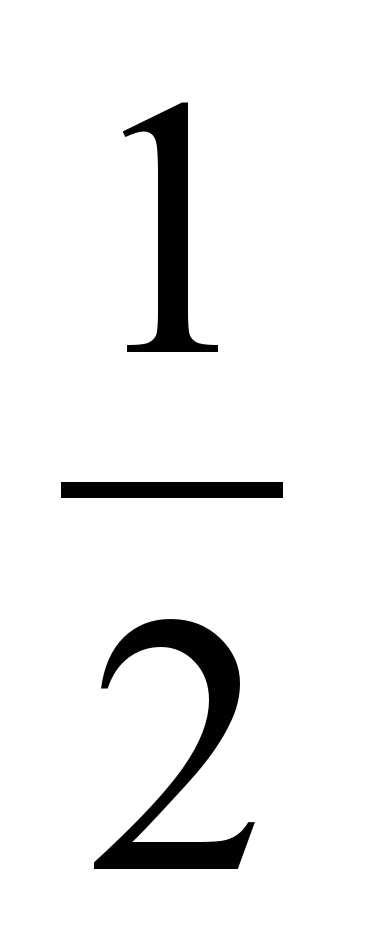 = =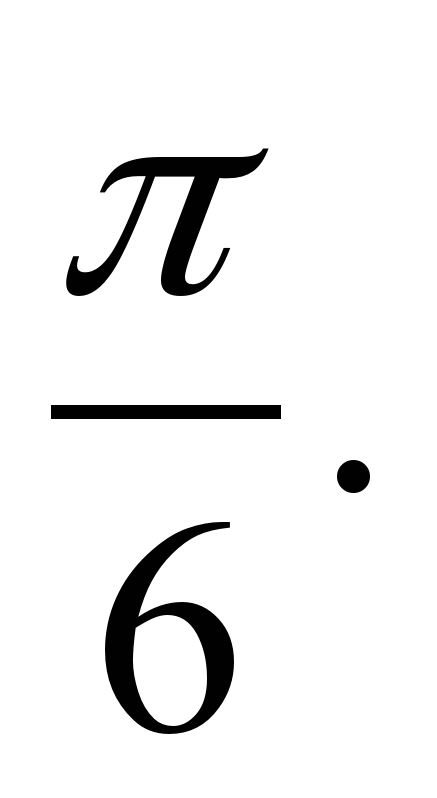 Пример 2. Вычислите arcsin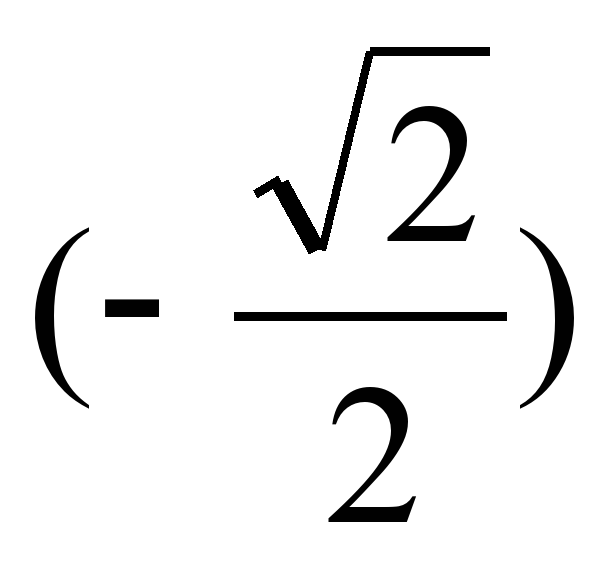 . .
Пример 3. Вычислите arcsin 0.
5) Доказать теорему и рассмотреть её применение на практике. Теорема. Для любого а [-1;1] выполняется равенство arcsin a + arcsin (-a) =0. [-1;1] выполняется равенство arcsin a + arcsin (-a) =0. Применение теоремы. На практике используется: arcsin (-a) = - arcsin a , где 0 ≤ а ≤ 1. Пример. arcsin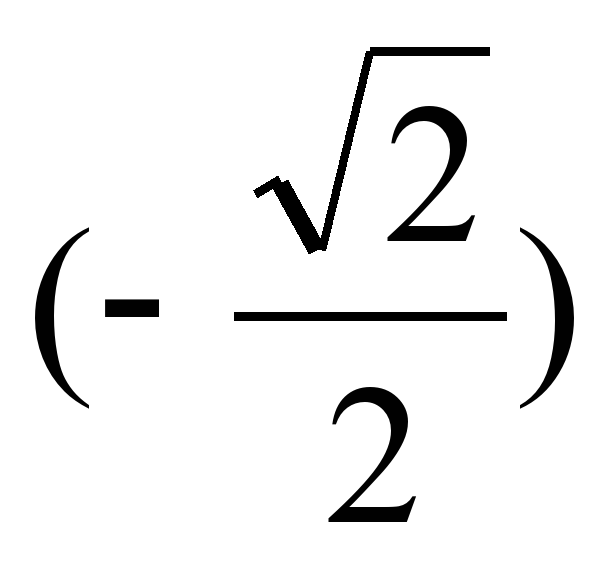 = - arcsin = - arcsin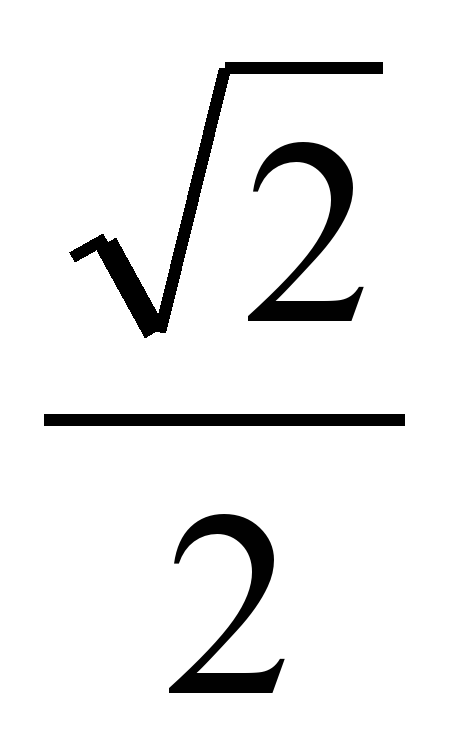 = - = - 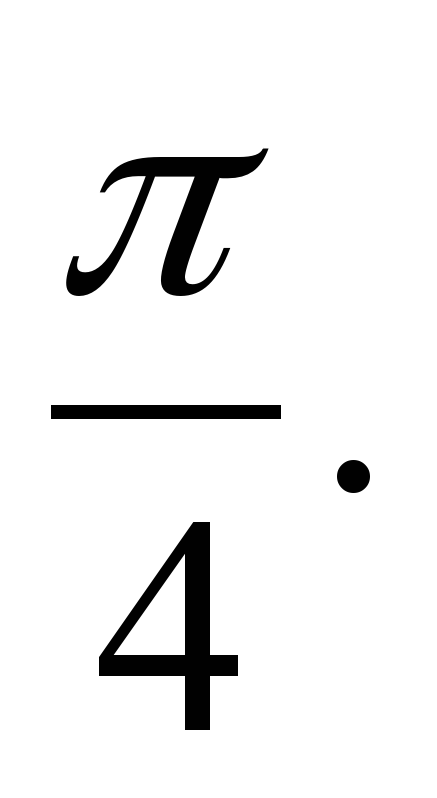 6) Сделать общий вывод о решении уравнения sin t = a . Если │a│≤ 1, то уравнение sint = a имеет решения: 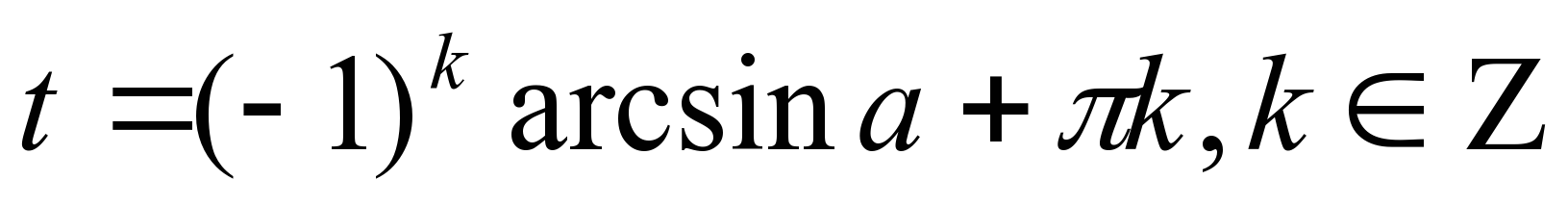 . . 7) Рассмотреть частные случи. Выделим формулы для решения следующих уравнений: sin t = 0, sin t =1 , sin t = –1. | 26 |
Слайд №4 Формулирует задание, показывает решение обсуждая каждое действие с учащимися.
Слайд №5
Слайд №6
Слайд №7 Формулирует вопрос.
Слайд №8 Показывает решение уравнения обсуждая каждое действие с учащимися.
Слайд №9 Формулирует вопрос.
Слайд №10
Слайд №11 Показывает решение обсуждая каждое действие с учащимися.
Слайд №12 Показывает решение
Слайд №13 Показывает решение.
Слайд №14 Доказывает теорему.
Слайд №15 Показывает применение теоремы на практике.
Слайд №16-17
Слайд №18
|
Отвечают на вопрос.
Работают в форме диалога с учителем, оформляют решение в тетради
Выполняют записи в тетради.
Записывают определение.
Работают в форме диалога с учителем, оформляют решение в тетради.
Записывают определение.
Записывают определение.
Работают в форме диалога с учителем, оформляют решение в тетради.
Один из учеников комментирует решение, остальные проверяют своё решение.
Выполняют записи в тетради.
Выполняют записи в тетради.
Выполняют записи в тетради.
Выполняют записи в тетради.
|
| VI | Обобщение изученного материала. Составим алгоритм решения простейшего тригонометрического уравнения вида sin t = a:
Пример 1. Решить уравнение sin t = 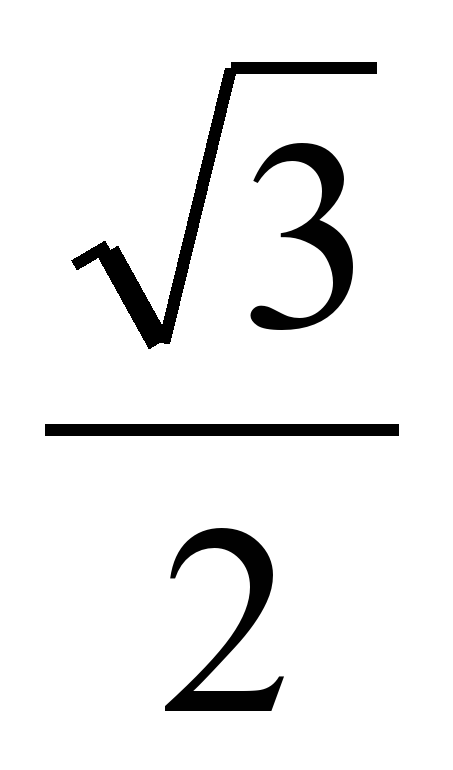 . . Пример 2. Решить уравнение sin t = 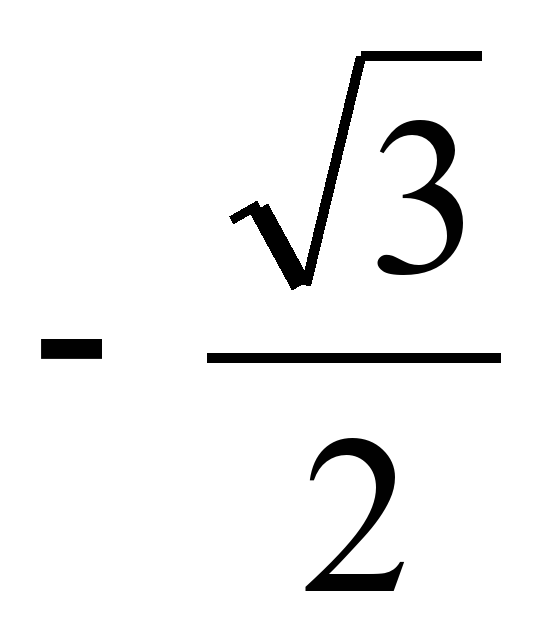 . . Пример 3. Решить уравнение sin t = 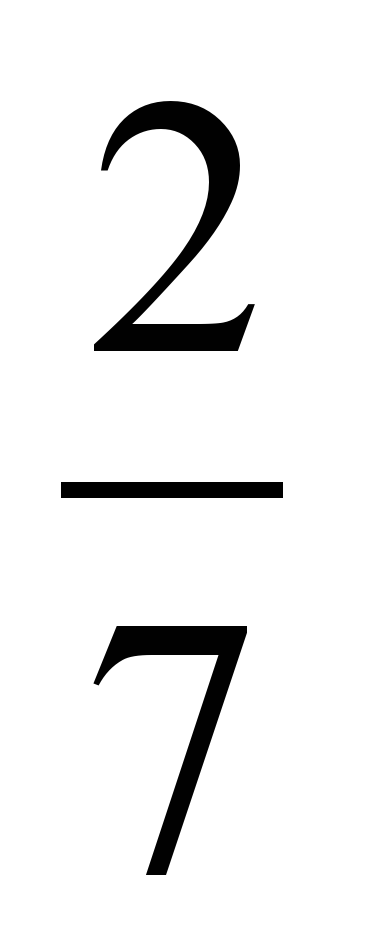 . . Пример 4. Решить уравнение sin t = - 1,2.
| 10 |
Показывает решение уравнений на примерах.
Слайд №19
Слайд №20-21 Слайд №22
Слайд №23 |
Работают в форме диалога с учителем, оформляют решение в тетради.
|