| Раздел 11.В. Уравнения и неравенства Тема: Иррациональные уравнения | Школа: НИШ ХБН г. Атырау
|
| Дата:
| Учитель математики: Адилгалиева Ж.С
|
| Класс: 11g Урок: | Количество присутствующих: 10 | Количество отсутствующих: |
| Ожидаемые результаты данного урока | АУ11.4. умеет выводить алгоритмы решения иррациональных уравнений и неравенств вида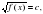 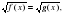 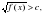 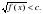
АУ 11.5.Применяет алгоритмы решения иррациональных уравнений и неравенств вида 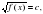 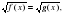 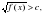 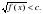 |
| Цели урока
| проверить знания корня n-ой степени, ввести понятие иррациональных уравнений и показать способы их решения. Проверить степень усвоения учащимися материала |
| Языковые цели
| Учащиеся: используют и понимают математические термины для описания решения иррациональных уравнений и неравенств. Предметная лексика и терминология Уравнение, неравенство. Рациональный, иррациональный. Радикал. Решать, решение, постороннее решение. Серия полезных фраз для диалога/письма Решить / я решил (а) иррациональное уравнение, путем избавления от радикала... . Убедитесь, что вы исключили посторонние корни. |
| Критерии успеха
| Учащийся достиг цели, если Выводит алгоритмы решения иррациональных уравнений и неравенств. |
| Ценности для реализации общенациональной идеи «
| Уважение, сотрудничество, открытость Привитие ценностей осуществляется посредством/через парную и групповую виды работ. Сотрудничество (формирование умения работать в группах, формировать навыки самоконтроля) |
| Навыки использования ИКТ
| Учащиеся могут использовать ресурсы сайта BilimLand для закрепления знаний |
| Первоначальные знания |
|
| Ход урока |
| Этапы урока Planned timings | Запланированная деятельность на уроке Planned activities
| Ресурсы Resources |
| Организационный этап 3-4 мин
| Актуализация знании. Повторение пройденного материала Организационный момент устанавливает личностный контакт учителя с учениками через формирование целей урока, их взаимного принятия и включение мотива на совместную работу. Положительная мотивация достигается анализом успешной работы учащихся с внешними углами треугольника. Создание благоприятной психологической среды. Приветствие учащихся. Добрый день, ребята! На столах у вас по три смайлика, выберите тот, который соответствует вашему настроению. - Как много улыбок засветилось. Спасибо! -А это моё настроение… Я готова продуктивно сотрудничать с вами. Удачи! |
|
| Терминология - 2 мин
| Учитель совместно с учениками проговаривают термины на трех языках.
|
|
| 2. Актуализация знаний мин
| | «Показательные уравнения и неравенства» 1.Решить уравнение: 1)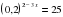 ; 2) ; 2) . . | 2.Решить неравенство  . . 3.Решить систему уравнений 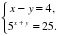
4.Решить неравенство: 1) ; 2) ; 2)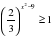 . . 5.Решить уравнение 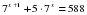 . . |
|
| Организация первичного контроля Индивидуальная работа 10 мин
| Определение. Уравнения, в которых под знаком корня содержится переменная, называют иррациональными. Из предложенных уравнений назовите номера тех, которые являются иррациональными. 1) 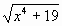 =10; =10; 2) 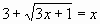 3)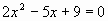 ; ; 4) 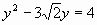 ; ; 5)  ; ; 6) 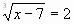 ; ; 7) 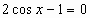 ; ; 8) 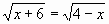 ; ; Верные ответы дают год рождения Георга Римана-1826. Решим данные иррациональные уравнения. Ход решения объясняют у доски ученики, подготовленные учителем заранее. 1-ый ученик: 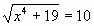
Возведём обе части уравнения в квадрат, получим: 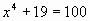 ; ;
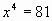 ; ;
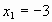 , , 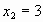
Проверка. Если 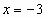 , то , то 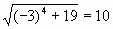 , Если , Если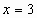 , то , то 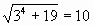 , , 10=10-верно. 10=10-верно. Значит,  корень уравнения. Значит, корень уравнения. Значит,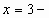 корень уравнения. корень уравнения. Ответ. -3;3. 2-ой ученик: 1-ый способ решения. 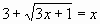 , ,
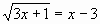 , ,
Возведём обе части уравнения в квадрат, получим:  , ,
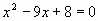 , ,
 , , 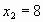
Проверка. Если 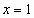 , то , то 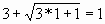 , Если , Если  , то , то  , , 5 = 1 - неверно. 8 = 8 - верно. Значит, 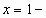 посторонний корень. Значит, посторонний корень. Значит, 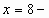 корень уравнения. корень уравнения. Ответ.  . . 2-ой способ решения (объясняет учитель). 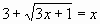 , ,
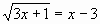
Может ли выражение в правой части быть отрицательным? Перейдём к смешанной системе:      
Ответ.  Уравнение 8) решаем самостоятельно (ученик за доской) с последующей проверкой. 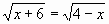
  
Ответ.  Вывод. 1) Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путём возведения в степень обеих частей уравнения. 2) При возведении обеих частей уравнения в чётную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.
|
Учащиеся отрабатывают практические навыки
|
| Формирование новых знаний учащихся. 10 мин Работа в группе | | После выполнения задания учащиеся меняются тетрадями и проводят взаимопроверку с последующим выставлением отметок в лист взаимооценивания.
|
|
Этап закрепления изученного материала. Первичное закрепление (10мин) Цель этапа: проговаривание и закрепление нового знания; выявить пробелы первичного осмысления изученного материала, неверные представления уч-ся
| Самостоятельная работа. Слайд 11. После решения и сдачи самостоятельных работ на слайде появляются ответы.
| учащимся предоставляется следующее задание – выполнение тестовой работы. Всего в задании пять примеров, за каждый правильный пример, учащаяся получает один балл. Далее, после выполнения задания, учитель совместно с учащимися проводит взаимопроверку заданий. Затем, каждая учащаяся ставит отметку в лист взаимооценивания |
|
Рефлексия (2мин)
| Домашнее задание. Home Task. Приложение 2 Подведение итогов урока. Рефлексия.Reflection Рефлексия. Учащиеся дополняют следующие пред.ложение: Сегодня на уроке я научился… Сегодня на уроке мне понравилось… Сегодня на уроке я повторил… Сегодня на уроке я закрепил… Сегодня на уроке я поставил себе оценку …
|
|
| Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности |
| Совместная работа это главная тщательно запланированная работа, так что Учащиеся менее уверенные работают с такими же как своего уровня, но очень уверенными. Диалог между партнерами таков, что оба учатся одновременно, а не так чтобы кто-то зависел от другого.
| Наблюдение Опрос Вопросы на понимание Взаимооценивание Самооценивание Рефлексия
| Здоровьесберегающие технологии. Используемые физминутки и активные виды деятельности. Пункты, применяемые из Правил техники безопасности на данном уроке. |
| Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. |
| Цели были реализованы, ожидаемый результат подтвержден. Учащийся знают и умеют решать показательные уравнения и неравенства. Атмосфера доброжелательная, рабочая. Во времени уложились. Изменения в план не вносились. |
| Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|
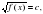
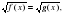
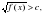
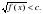
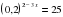 ; 2)
; 2) .
. .
.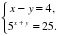
 ; 2)
; 2)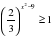 .
.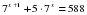 .
.















