Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №24 с углубленным изучением иностранных языков» муниципального образования городской округ Симферополь Республики Крым
Тема урока: Решение задач с
помощью квадратных уравнений.
8 класс. Алгебра.
Учитель математики:
Сулейманова А.Р.
2014-2015 уч.год
Цели урока:
выработать умение применять квадратные уравнения для решения алгебраических и геометрических задач; продолжить формирование практических и теоретических умений и навыков по теме “Квадратные уравнения”;
способствовать умению анализировать условие задач, развитию умения рассуждать, развитию познавательного интереса, умению видеть связь между математикой и окружающей жизнью;
воспитывать внимательность и культуру мышления, самостоятельность и взаимопомощь.
Тип урока: комбинированный.
Оборудование: учебник.
План урока:
1) Тема урока. Постановка целей урока.
2) Актуализация знаний (Самостоятельная работа).
3) Составление опорной схемы действий.
4) Решение задач по схеме.
5) Практикум по решению уравнений.
6) Подведение итогов. Рефлексия.
7) Домашнее задание.
Ход урока
1х30
Организационный момент.
Постановка целей урока.
Проверка домашнего задания.
№534. Решите уравнение:
в)  D=169-4*3*14=1;
D=169-4*3*14=1;
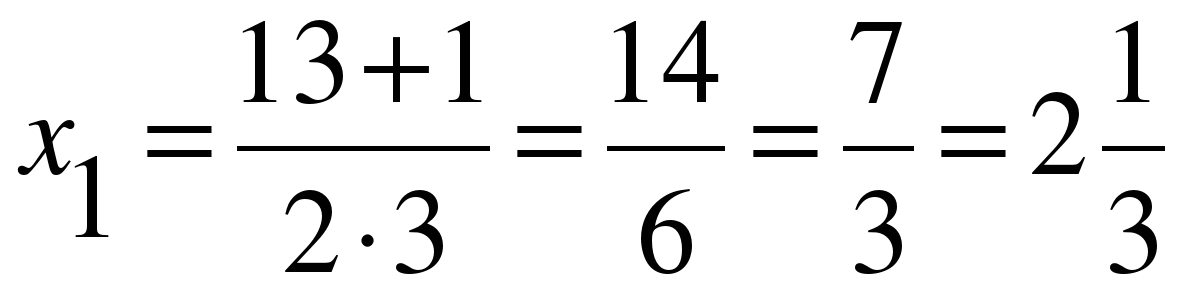 ;
; 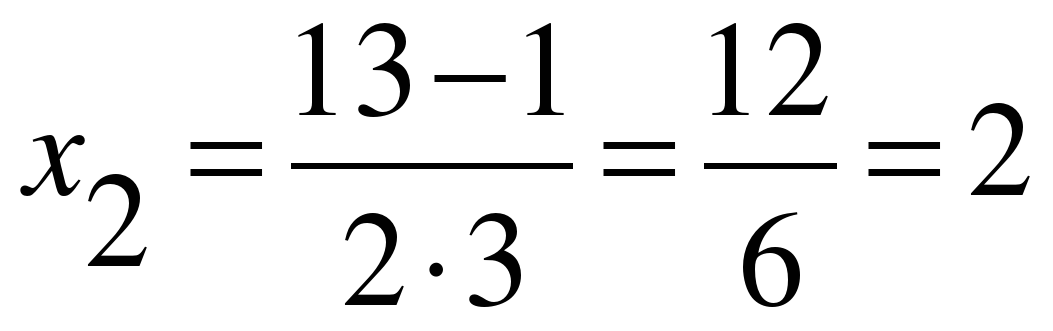 .
.
г) 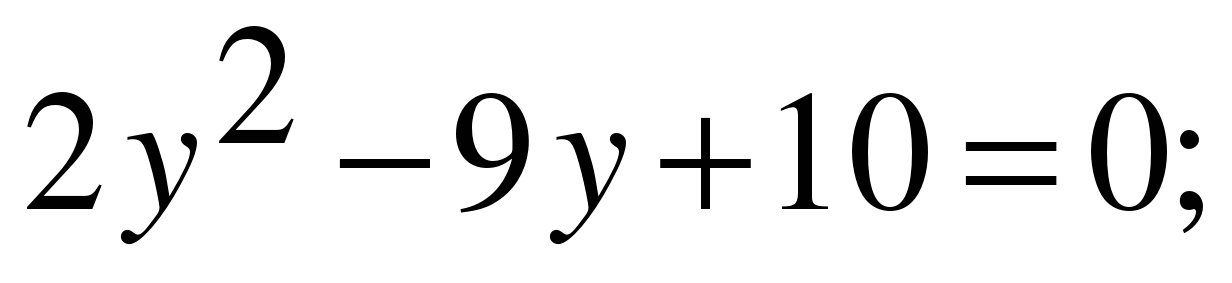 D=81-4*2*10=1;
D=81-4*2*10=1;
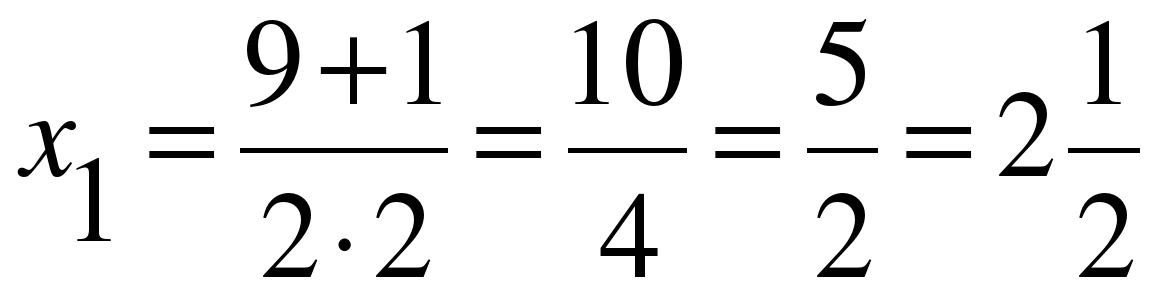 ;
; 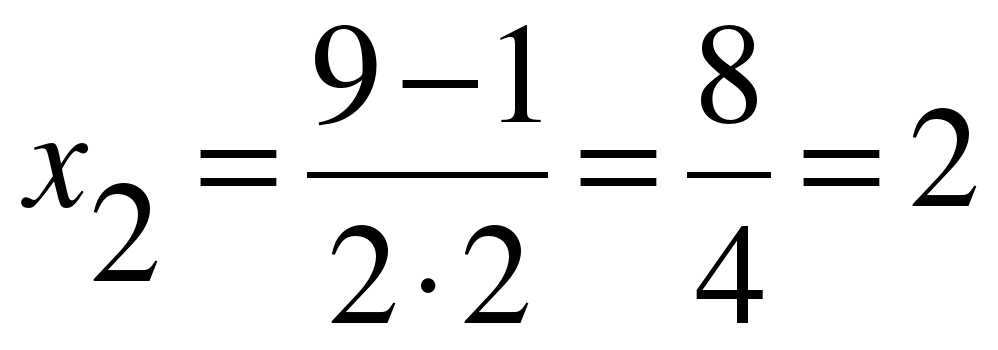 .
.
№535. Решите уравнение:
в) 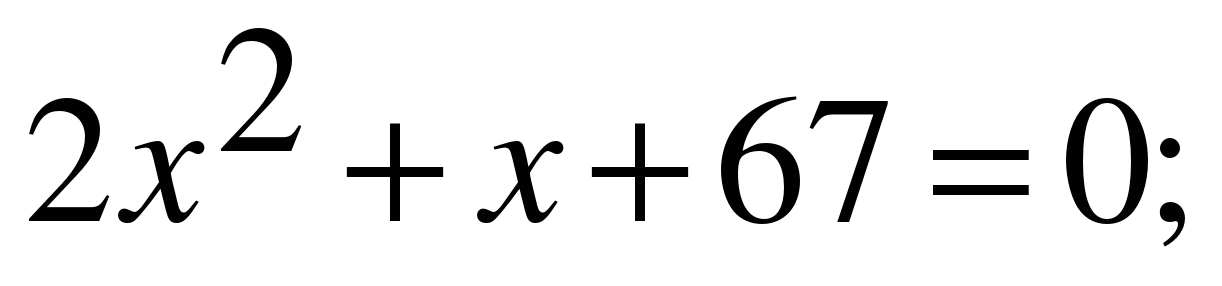 D=1-4*2*67=-535;
D=1-4*2*67=-535;
Уравнение корней не имеет, так как дискриминант отрицательный.
г) 
D=324-4*1*81=0;
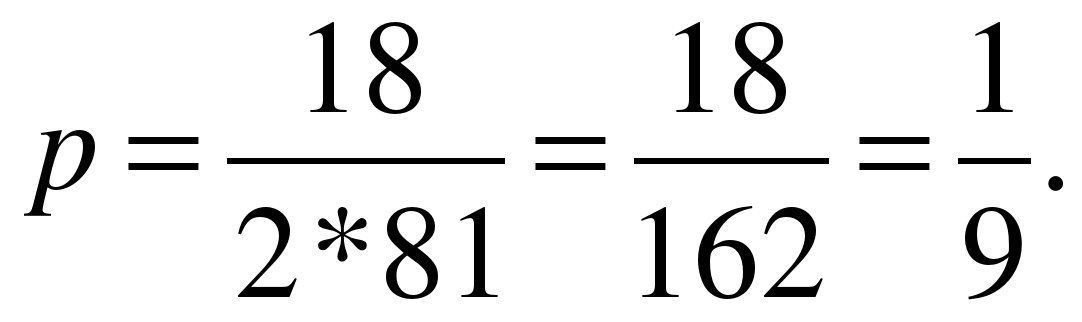
№539. Решите уравнение:
в) 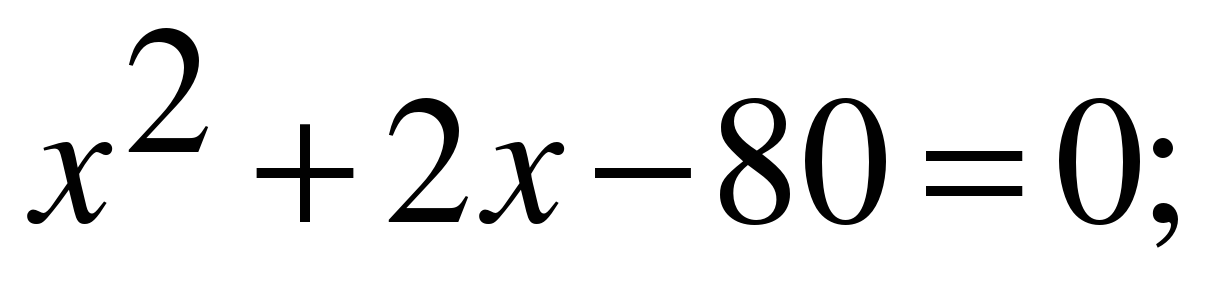 D=4-4*1*(-80)=324;
D=4-4*1*(-80)=324;
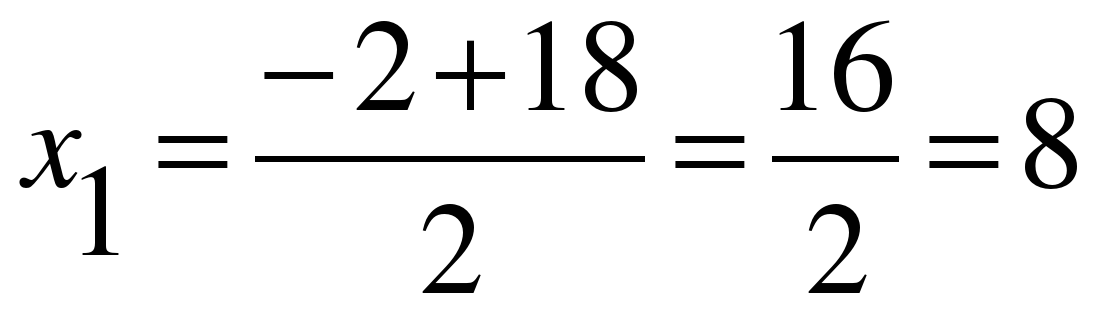 ;
; 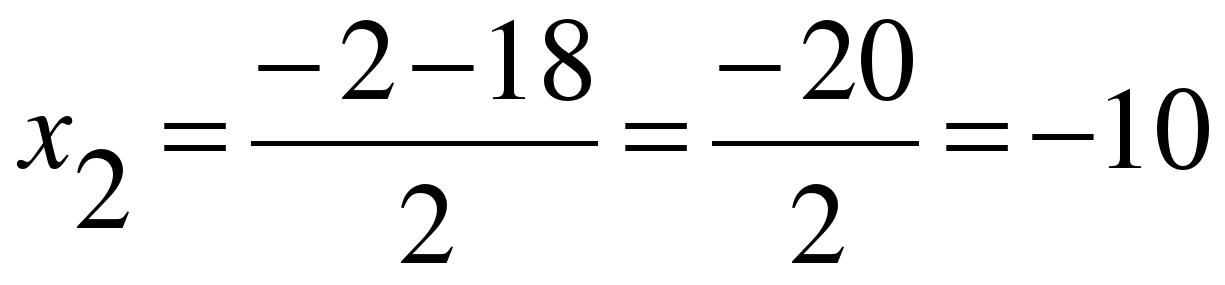 .
.
г) 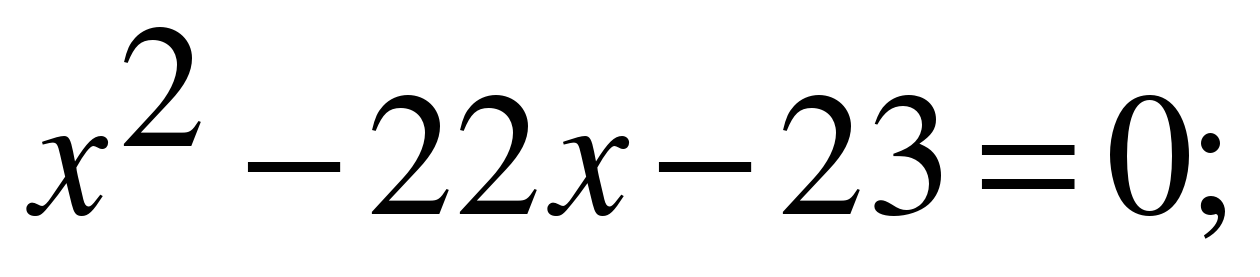 D=484-4*1*(-23)=576;
D=484-4*1*(-23)=576;
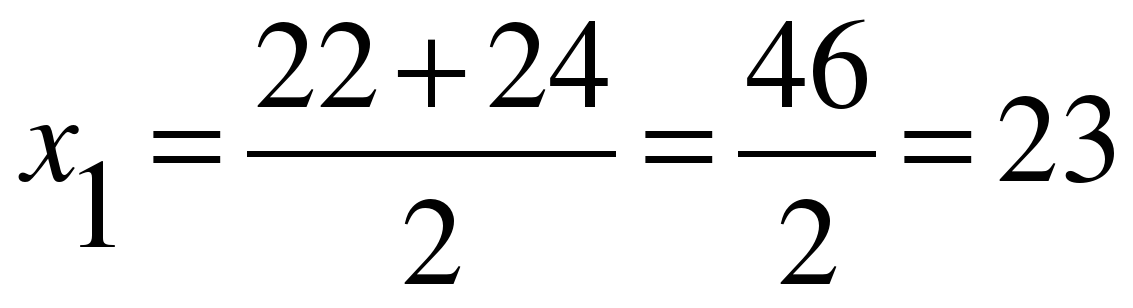 ;
; 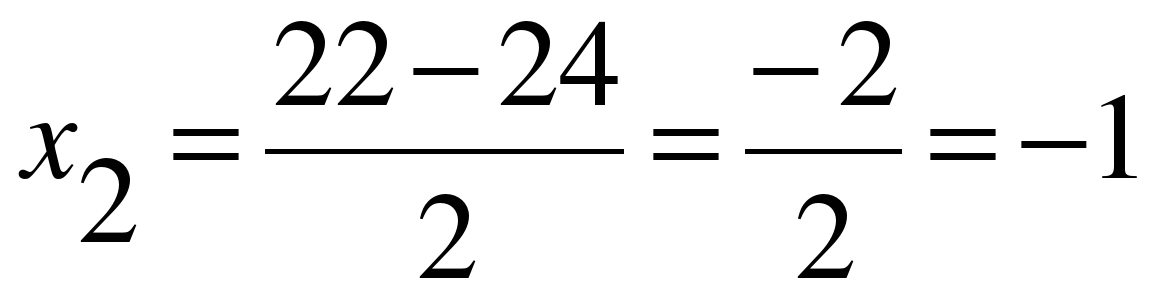 .
.
д) 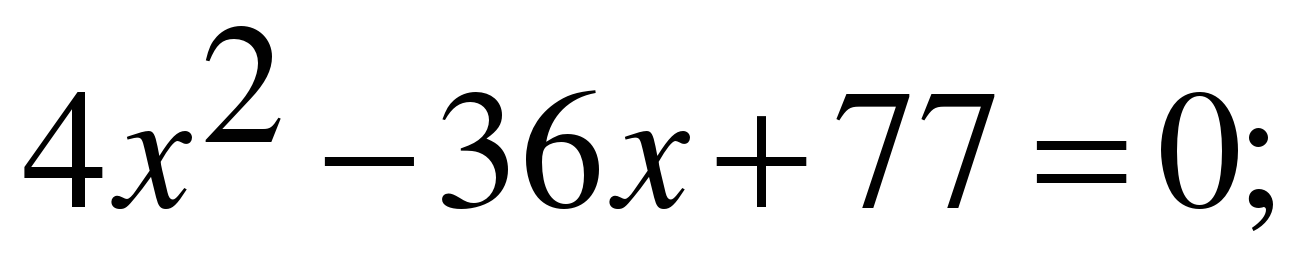 D=1296-4*4*77=64;
D=1296-4*4*77=64;
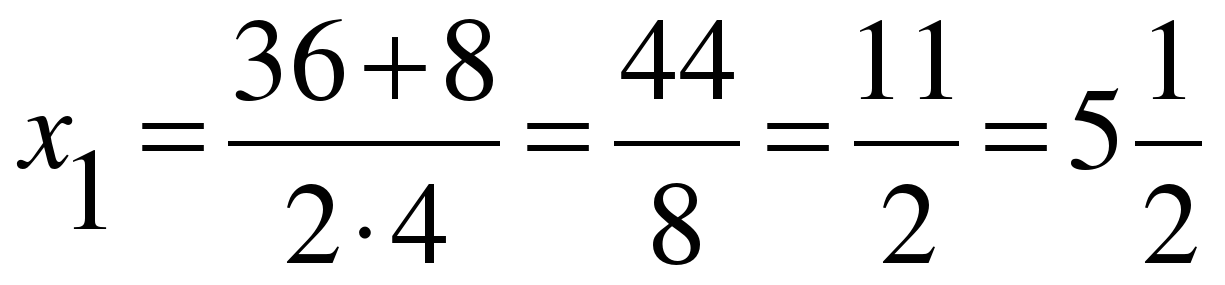 ;
; 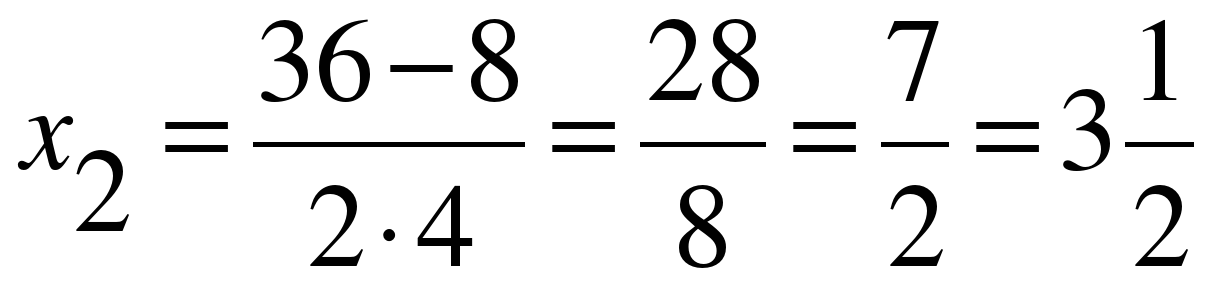 .
.
Контроль усвоения материала.
Вариант 1.
Заполните таблицу:
| Уравнение | а | в | с | в2-4ас | х1 | х2 | х1+х2 | х1*х2 |
| х2-6х+9=0 | | | | | | | | |
| | 2 | 7 | 9 | | | | | |
| 4х2=-7х | | | | | | | | |
Вариант 2.
Заполните таблицу:
| Уравнение | а | в | с | в2-4ас | х1 | х2 | х1+х2 | х1*х2 |
| 5х2-4х=0 | | | | | | | | |
| | 3 | 0 | -27 | | | | | |
| -2х2=-5-3х | | | | | | | | |
Физкультминутка.
2х30
Изучение нового материала.
Многие задачи алгебры, геометрии, физики, техники приводят к необходимости решения квадратных уравнений.
Мы с вами должны научиться проводить анализ задачи, вводить неизвестные величины, находить зависимость между данными задачи и неизвестными величинами.
Составление схемы действий.
Анализ условия
Выделение главных ситуаций
Введение неизвестных величин
Установление зависимости между данными задачи и неизвестными величинами
Составление уравнения
Решение уравнения
Запись ответа
Если в уравнении дискриминант положителен, решениями задачи могут быть оба корня уравнения. Иногда бывает, что по смыслу задачи ей удовлетворяет лишь один из корней квадратного уравнения.
Решение упражнений.
№559. Произведение двух натуральных чисел, одно из которых на 6 больше другого, равно 187. Найдите эти числа.
Решение.
Пусть х - одно натуральное число, тогда (х+6) – второе натуральное число. Зная, что произведение чисел равно 187, составим уравнение:
х(х+6)=187;
х2+6х-187=0;
D=784;
x1=11, x2=-17.
Второй корень по смыслу задачи не подходит, т.к. даны натуральные числа. Значит меньшее число равно 11. Второе число равно 11+6=17.
Ответ: 11 и 17.
№561. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 см больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м2.
Решение.
Пусть х см – длина одной стороны огородного участка, тогда (х+10) см – длина второй стороны. Так как площадь участка равна 1200 м2, составим уравнение:
х(х+10)=1200;
х2+10х-1200=0;
D=4900;
x1=30, x2 =-40 (не удовлетворяет условию задачи),
тогда вторая сторона равняется:
30+10=40.
Найдем длину всей изгороди:
Р=(30+40)*2=140 (м).
Ответ: 140м.
№563. Найдите катеты прямоугольного треугольника, если известно, что их сумма равна 23 см, а площадь данного треугольника равна 60 см2.
Решение.
Пусть х см – длина одного катета прямоугольного треугольника, тогда (23 – х) см – длина второго катета. Зная, что площадь прямоугольного треугольника равна половине произведения катетов и составляет 60 см2, составим уравнение:
1/2· х · (23 – х) = 60;
х (23 – х) = 120;
23х – х2 – 120 = 0;
х2 – 23х + 120 = 0;
D = (–23)2 – 4 · 1 · 120 = 529 – 480 = 49; D 0; 2 корня.
x1 = 15;
x2 = 8.
Оба корня удовлетворяют условию задачи.
О т в е т: 8см, 15см.
Физкультминутка.
3х30
Решение упражнений.
№564. Произведение двух последовательных натуральных чисел больше их суммы на 109. Найдите эти числа.
Решение.
Пусть х – первое натуральное число, тогда (х+1) – второе натуральное число. Так как произведение этих натуральных чисел больше их суммы на 109, составим уравнение:
х (х+1) = 109 + х + х+1;
х2 + х = 109 + 2х +1;
х2 – х - 110 = 0;
D = (–1)2 – 4 · 1 · (-100) = 441; D 0; 2 корня.
x1 = 11;
x2 = 12.
Ответ: 11; 12.
№567. В прямоугольном треугольнике один из катетов на 3 см меньше гипотенузы, а другой – на 6 см меньше гипотенузы. Найдите гипотенузу.
Решение.
Пусть х см – один из катетов в прямоугольном треугольнике, а второй катет (х-3) см, тогда гипотенуза равна (х+3) см. Так как в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, составим уравнение:
х2 + (х - 3)2 = (х + 3)2;
х2 + х2 – 6х + 9 = х2 + 6х + 9;
х2 – 12х = 0;
х (х – 12) = 0;
x1 = 0; (не имеет смысла данное решение)
x2 = 12 (см) – первый катет;
12 + 3 = 15 (см) – гипотенуза треугольника.
Ответ: 15 см.
Дополнительное задание.
№568. В кинотеатре число мест в ряду на 8 больше числа рядов. Сколько рядов в кинотеатре, если всего в нем имеется 884 места?
Решение.
Пусть х – число рядов в кинотеатре, тогда (х + 8) – число мест в ряду. Количество мест в кинотеатре равно х · (х + 8). Зная, что всего в кинотеатре 884 места, составим уравнение:
х · (х + 8) = 884;
х2 + 8х – 884 = 0;
D = 82 – 4 · 1 · (–884) = 64 + 4 · 884 = 3600; D 0; 2 корня.
x1 = 26;
x2 = –34 – не удовлетворяет условию задачи.
О т в е т: 26 рядов.
Рефлексия
Учащиеся заполняют таблицу на карточке. В соответствующей ячейке таблице ставится «галочка» или знак «+».
| | Нет | Не очень
хорошо | Хорошо | Отлично, без ошибок |
| Знаю формулы для решения уравнений | | | | |
| Понимаю, как решать уравнения. Знаю алгоритм. | | | | |
| Умею решать квадратные уравнения. | | | | |
Домашнее задание: п. 23, читать, № 560, 562, 565.