Цель:
Помочь ученикам в сдаче единого национального тестирования. Обеспечить всей необходимой информацией.
Еще раз напоминаю, что оптимальное время выполнения тестового задания ЕНТ по математике составляет 37,5 минуты. Значит, на решение каждого тестового задания следует тратить не боле 1,5 минуты. Поэтому покажу некоторые практические приемы решения тестовых заданий ЕНТ, которые позволяют очень быстро находить правильные ответы. Здесь важны не только каждая минута, но и секунда. Предлагаю рассмотреть некоторые решения тестовых заданий ЕНТ.
Просмотр содержимого документа
«Уровень А»
Уровень А
1) Перечислите в ответе номера верных равенств.
1:45=45
1,4⋅37=0,6
0,51−34=0,2
0,7+35=1,3
A) 4 B) 2 C) 1 И 2 D) 2 И 4
Решение:
Утверждение под номером 1 неверно, так как 1:45=1⋅54=54≠45.
Утверждение под номером 2 верно, действительно, 1,4⋅37=1410⋅37=2⋅310⋅1=0,6.
Утверждение под номером 3 неверно, поскольку 0,51−34=12:(1−34)=12:14=12⋅41=2≠0,2
Утверждение под номером 4 верно, так как 0,7+35=710+35=7+610=1310=1,3
2) На координатной прямой отмечено число x

Какое из следующих неравенств верно?
x² 1
x−12
x−1≥0
x+5
A) 4 B) 2 C) 1 D) 3
Решение:
По рисунку видно, что число x находится между 0 и 1 ближе к 1, поэтому 0,5x1.
Первое неравенство неверно: если положительное число меньше 1, то и его квадрат меньше 1.
Второе неравенство неверно: число x больше 0,5, поэтому при вычитании из x числа 0,5 получится положительный результат.
Третье неравенство неверно: число x меньше 1, поэтому при вычитании из x числа 1 получится отрицательный результат.
Четвертое неравенство верно: действительно, если к 5 прибавить число, меньшее 1, то получится число, меньшее 6.
3) Какая из прямых, изображенных на рисунке, является графиком функции y= − 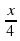 ?
?
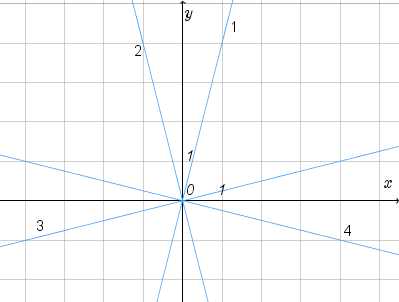
A) 4 B) 2 C) 1 D) 3
Решение:
Нам дано уравнение функции y=− 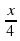 . При x=1 значение y=−
. При x=1 значение y=− 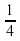 . Точка с координатами (1;−
. Точка с координатами (1;− 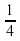 ) лежит на графике под номером 4. Другие графики ее не содержат.
) лежит на графике под номером 4. Другие графики ее не содержат.
4) Дана арифметическая прогрессия 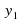 =−3
=−3 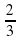 ,
,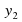 = −1
= −1 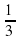 ,… Найдите сумму первых шести членов этой прогрессии.
,… Найдите сумму первых шести членов этой прогрессии.
A) 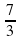 B)
B)  C) 13 D) -13
C) 13 D) -13
Решение:
Напомним, что арифметическая прогрессия - это последовательность чисел, в которой каждое следующее число, начиная со второго (y2), получается из предыдущего члена последовательности добавлением к нему постоянное число d, называемое разностью арифметической прогрессии. Нам даны первый и второй члены арифметической прогрессии.
Для удобства вычислений запишем их в виде дробей:
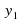 =−3
=−3 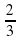 =−
=− 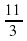 ,
, 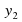 =−1
=−1 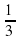 =−
=−  .
.
Найдем разность прогрессии, вычтя из второго члена прогрессии первый.
d=−  −(−
−(−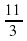 )=−
)=−  +
+ 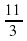 =
= 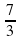 .
.
Вычислив разность прогрессии, для нахождения суммы первых шести членов прогрессии можно было воспользоваться формулой Sn=[(2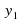 +(n−1)d)∕2]⋅n, где
+(n−1)d)∕2]⋅n, где 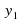 - первый член арифметической прогрессии, d - разность прогрессии, n - количество суммируемых членов.
- первый член арифметической прогрессии, d - разность прогрессии, n - количество суммируемых членов.
В нашем случае 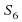 =[(2⋅(−
=[(2⋅(−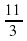 )+(6−1)⋅
)+(6−1)⋅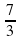 )∕2]⋅6=(−
)∕2]⋅6=(− 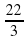 +
+ 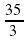 )⋅3=13.
)⋅3=13.
Один из углов равнобедренного треугольника равен 100 ̊. Найдите любой другой его угол. Ответ дайте в градусах.
A) 80 ̊ B) 40 ̊ C) 20 ̊ D) 100 ̊
Решение:
Угол 100 ̊ - тупой и поэтому не может быть углом при основании равнобедренного треугольника. Значит, это угол при вершине.
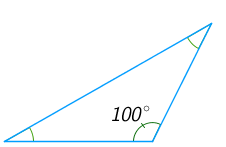
Тогда на два угла при основании приходится 180 ̊−100 ̊=80 ̊. Поэтому угол при основании равен 80 ̊:2=40 ̊.
Просмотр содержимого документа
«Уровень В»
Уровень В
Диагонали ромба равны 24 и 7,5. Найдите его площадь.
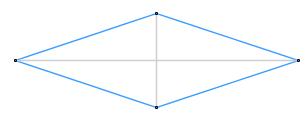
A) 180 B) 22,5 C) 90 D) 100
Решение:
Вспомним формулу для вычисления площади четырехугольника через его диагонали 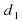 и
и 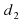 и угол α между ними: S =
и угол α между ними: S = 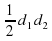 sinα. Угол между диагоналями ромба равен 90 ̊, поэтому его площадь равна S=
sinα. Угол между диагоналями ромба равен 90 ̊, поэтому его площадь равна S=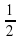 ⋅24⋅7,5⋅sin90 ̊=12⋅7,5⋅1=90.
⋅24⋅7,5⋅sin90 ̊=12⋅7,5⋅1=90.
После того, как цены на посуду в магазине были подняты на 20%, чашка стала стоить 132 тг. Сколько тенге стоила чашка до повышения цены?
A) 180 B) 158 C) 110 D) 112
Решение:
До повышения цены стоимость чашки составляла 100%, а после повышения цены – 120%. Обозначив за x руб.– начальную цену чашки в рублях, составим пропорцию:
x тг :100%=132 тг :120%
Найдем x:
x=132⋅100 :120=110.
До повышения цены чашка стоила 110 тг.
Решите уравнение 3x−7+2(3−x)=−x+8
A) 7 B) 4, 5 C) 9 D) 3
Решение:
3x−7+2(3−x)=−x+8
Раскроем скобки и приведем подобные слагаемые:
3x−7+6−2x=−x+8
x−1=−x+8.
Перенесем слагаемые, содержащие неизвестную x, в левую часть, не содержащие x – в правую, меняя при этом знак.
x+x=8+1
2x=9
x=4,5.
Выписаны первые несколько членов геометрической прогрессии: 1,5;−3; 6; …. Какое из следующих чисел есть среди членов этой прогрессии?
A) 9 B) -12 C) -9 D) 12
Решение:
Напомним, что геометрическая прогрессия - это последовательность чисел, в которой каждое следующее число, начиная со второго (b2), получается из предыдущего члена последовательности умножением его на постоянное число q, называемое знаменателем геометрической прогрессии. 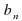 =
= ⋅q.
⋅q.
Знаменатель геометрической прогрессии можно найти, разделив любой ее член на предыдущий: q=−3:1,5=−2.
Каждый следующий член прогрессии получается из предыдущего умножением на −2. Запишем несколько первых членов данной прогрессии 1,5; −3; 6; −12… Мы и нашли, что число −12 есть среди членов прогрессии.
Расстояние между двумя селами равно 10 км. Два человека выходят одновременно из одного села в другое, причем первый за час проходит на 3 км больше второго. Определите скорость первого, если известно, что он приходит в пункт назначения на 3 часа раньше второго. Ответ дайте в км/ч.
A) 2 B) 5 C) 7 D) 3
Решение:
|
| Скорость(V) | Время(t) | Расстояние(S) |
| 1 | Х+3 | 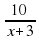
| 10 |
| 2 | х | 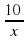
| 10 |
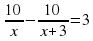
10(х+3)- 10х=3х(х+3)
10х+30-10х=3х²+9х
х²+3х-10=0
х=2км/ч- скорость второго
2+3=5 км/ч- скорость первого
Ответ: 5 км/ч.
Просмотр содержимого документа
«Уровень С»
Уровень С
1) Одна бочка содержит смесь спирта с водою в отношении 2 : 3, а другая – в отношении 3 : 7. Поскольку ведер нужно взять из каждой бочки, чтобы составить 12 ведер смеси, в которой спирт и вода были бы в отношении 3 : 5?
А) 8; 7 В) 3; 5 С) 5; 10 D) 9; 3 Е) 8; 3
Решение:
Пусть первая бочка содержит  ведер смеси спирта с водою, а вторая бочка -
ведер смеси спирта с водою, а вторая бочка - 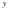 ведер смеси спирта с водою. Составим таблицу:
ведер смеси спирта с водою. Составим таблицу:
| п/п | I бочка | II бочка | Новая смесь |
| в частях | в ведрах | в частях | в ведрах | в частях | в ведрах |
| Спирт | 2 | 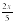
| 3 | 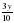
| 3 | 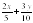
|
| Вода | 3 | 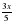
| 7 | 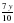
| 5 | 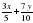
|
| Всего | 5 | 
| 10 | 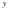
|
|
|
По условию: 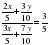
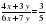 , по основному свойству пропорции имеем:
, по основному свойству пропорции имеем:
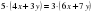
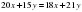
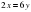 или
или
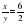
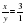
Новая смесь должна содержать 3 части I бочки и одну часть II бочки. Всего 3+1=4 части.
Так как новая смесь содержит 12 ведер, то на одну часть приходится:
12 (в) : 4 (ч) = 3 (в).
Тогда,
3 (в)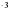 (ч)=9 (в)
(ч)=9 (в)
3 (в)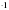 (ч)=3 (в)
(ч)=3 (в)
Ответ: D)
2) В трапеции ABCD AB=BC=CD. Точки K,L,M и N - середины сторон трапеции. Найдите наибольший угол четырёхугольника KLMN, если угол BAD равен 40 ̊. Ответ дайте в градусах.
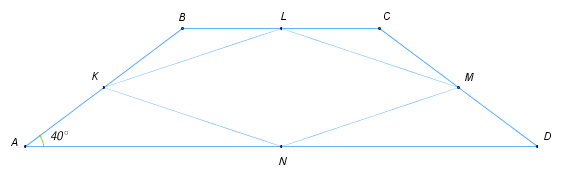
A) 40 ̊ B) 140 ̊ C) 20 ̊ D) 100 ̊
Решение:
Проведем диагонали AC и BD. KL и NM – это средние линии в треугольниках ABC и ADC соответственно, поэтому они параллельны стороне AC. Аналогично, LM и KN параллельны BD. Значит, стороны четырехугольника KLMN параллельны диагоналям трапеции, и поэтому, во-первых, этот четырехугольник – параллелограмм, во-вторых, его углы равны углам между диагоналями трапеции.
Теперь найдем углы между диагоналями трапеции. Данная нам трапеция особенная, в ней равны три стороны, и поэтому диагональ AC является биссектрисой угла A. Действительно, ∠BAC=∠BCA (это углы при основании равнобедренного треугольника ABC), но и ∠CAD=∠BCA (это накрест лежащие угла при параллельных прямых). Значит, углы BAC, CAD и BCA равны: ∠BAC=∠CAD=∠BCA=40 ̊:2=20 ̊.
Аналогично можно найти угол BDA – он тоже равен 20∘.
Пусть O – точка пересечения диагоналей трапеции. В треугольнике AOD два угла равны по 20 ̊, следовательно, углы между диагоналями трапеции равны 140 ̊ и 40 ̊. Значит, и углы четырехугольника KLMN равны тому же самому. Нам нужен наибольший угол – он равен 140 ̊.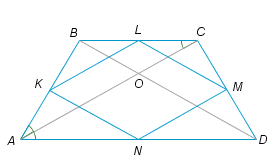
3) Какие из следующих утверждений верны?
Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.
Диагонали ромба пересекаются под прямым углом.
Диагонали прямоугольника пересекаются под прямым углом.
A) 4 и 3 B) 2 и 1 C) 1 и 2 D) 2 и 3
Решение:
Утверждение под номером 1 неверно. Вписанные углы, опирающиеся на одну хорду, но с разных сторон окружности, могут быть неравными (см. рис).

Утверждение под номером 2 верно: вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.
Утверждение под номером 3 верно: диагонали ромба перпендикулярны.
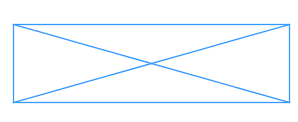
Утверждение под номером 4 неверно. Диагонали прямоугольника не обязательно перпендикулярны, например, у прямоугольника на рисунке диагонали явно не перпендикулярны.
Игральную кость бросают 2 раза. Найдите вероятность того, что выпавшие числа разной четности.
A) 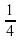 B)
B) 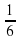 C)
C) 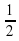 D)
D) 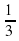
Решение:
Вероятность – это отношение количества благоприятных вариантов к количеству всех возможных вариантов.
На первой игральной кости может выпасть любое число от 1 до 6, и на второй тоже. Значит, всего вариантов выпадения двух костей 6⋅6=36.
Посчитаем благоприятные варианты, т.е. те, в которых выпавшие числа разной четности. Если на первой кости выпало четное число (а это три варианта: 2, 4 и 6), то на второй кости должно выпасть нечетное число (это тоже три варианта: 1, 3 и 5). Значит, всего 9 таких вариантов. И еще столько же вариантов, когда наоборот, на первой кости выпало нечетное число, а на второй четное. Следовательно, благоприятных вариантов всего 9+9=18.
Тогда искомая вероятность равна 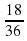 =0,5.
=0,5.
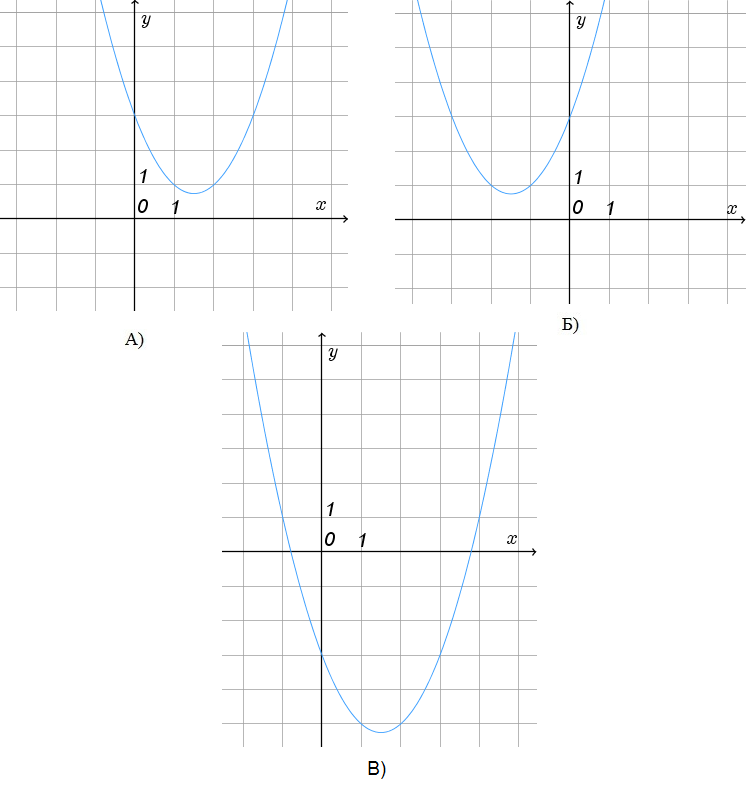
Установите соответствие между графиками и формулами.
1) y=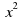 +3x−3; 2) y=
+3x−3; 2) y=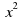 −3x+3; 3) y=
−3x+3; 3) y=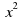 −3x−3; 4) y=
−3x−3; 4) y=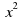 +3x+3
+3x+3
A) А: 2; Б: 4; В: 3
B) А: 3; Б: 1; В: 2
C) А: 1; Б: 4; В: 3
D) А: 2; Б: 4; В: 1
Решение:
Параболы А и Б не пересекают ось OX, значит, соответствующие квадратные трехчлены имеют отрицательный дискриминант.
Из четырех данных квадратный трехчленов таких ровно два – это второй и четвертый.
Парабола А проходит через точку (1;1). Подставим в уравнения 2 и 4 значение x=1, получим соответственно 1 и 7. Это означает, что парабола А задается уравнением 2, а парабола Б – уравнением 4.
График В проходит через точку (1;−5). Подставим значение x=1 в оставшиеся уравнения 1 и 3, получим соответственно 1 и −5. Это означает, что парабола В задается уравнением 3.

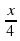 ?
?

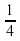 . Точка с координатами (1;−
. Точка с координатами (1;− 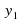 =−3
=−3 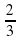 ,
,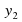 = −1
= −1 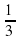 ,… Найдите сумму первых шести членов этой прогрессии.
,… Найдите сумму первых шести членов этой прогрессии.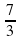

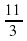 ,
,  .
. 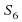 =[(2⋅(−
=[(2⋅(−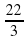 +
+ 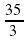 )⋅3=13.
)⋅3=13.

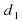 и
и 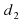 и угол α между ними: S =
и угол α между ними: S = 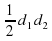 sinα. Угол между диагоналями ромба равен 90 ̊, поэтому его площадь равна S=
sinα. Угол между диагоналями ромба равен 90 ̊, поэтому его площадь равна S=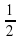 ⋅24⋅7,5⋅sin90 ̊=12⋅7,5⋅1=90.
⋅24⋅7,5⋅sin90 ̊=12⋅7,5⋅1=90.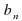 =
= ⋅q.
⋅q. 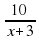
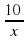
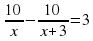
 ведер смеси спирта с водою, а вторая бочка -
ведер смеси спирта с водою, а вторая бочка - 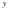 ведер смеси спирта с водою. Составим таблицу:
ведер смеси спирта с водою. Составим таблицу: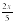
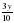
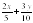
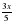
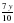
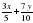
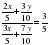
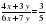 , по основному свойству пропорции имеем:
, по основному свойству пропорции имеем: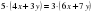
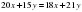
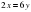 или
или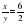
 (ч)=9 (в)
(ч)=9 (в) (ч)=3 (в)
(ч)=3 (в)



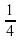 B)
B) 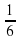
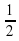
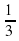
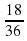 =0,5.
=0,5.
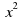 +3x−3; 2) y=
+3x−3; 2) y=















