Тесты по стереометрии

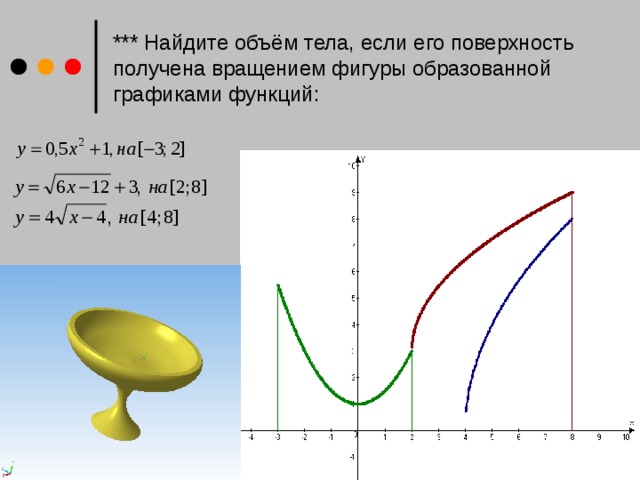
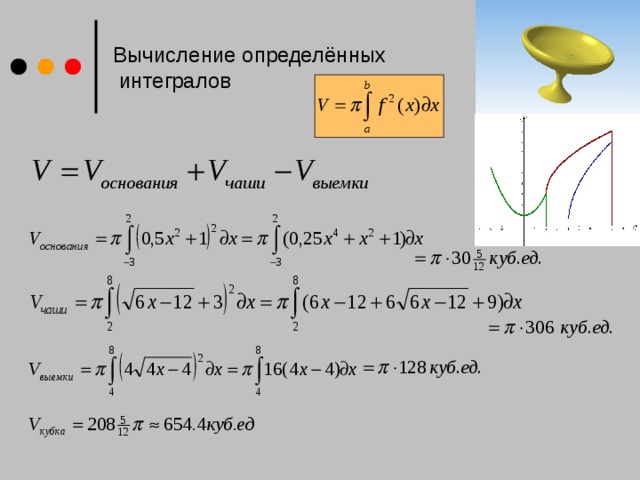
Тесты необходимы для проверки знаний по математике, поэтому нужно тестировать учеников для полной картины: поняли студенты темы или нет

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Тесты по стереометрии»

Вычисление объемов тел вращения

Применение интеграла

Преподаватель ГБПОУ “СПК” Тихонова Надежда Викторовна

Постановка задачи

y=f(x)

Пусть функция y = f(x) определена, неотрицательна и непрерывна на отрезке [a; b], тогда график кривой у= f(x) на [a; b], ось OX, прямые x = a, x = b образуют криволинейную трапецию.

Рассмотрим тело, образованное вращением этой криволинейной трапеции вокруг оси OX и найдем его объем.

Разобьем отрезок [a;b] на n частей произвольным образом, через каждую точку деления проведем плоскость, перпендикулярную к оси ОХ и найдём площади полученных поперечных сечений.

y=f(x)

Очевидно, что любое поперечное сечение тела вращения – круг. Радиус круга равен значению функции в х с

Площадь этого круга – S(x) = π · f 2 (x с )

Построим на каждом промежутке цилиндрическое тело, образующая которого параллельна оси ОХ, а основанием является сечение - круг.

Радиус круга равен значению функции в х с

Площадь этого круга –

S(x) = π f 2 (x с )

Объём цилиндра –

V=S(x)∙ Δx

y=f(x)

f(x с )

x с

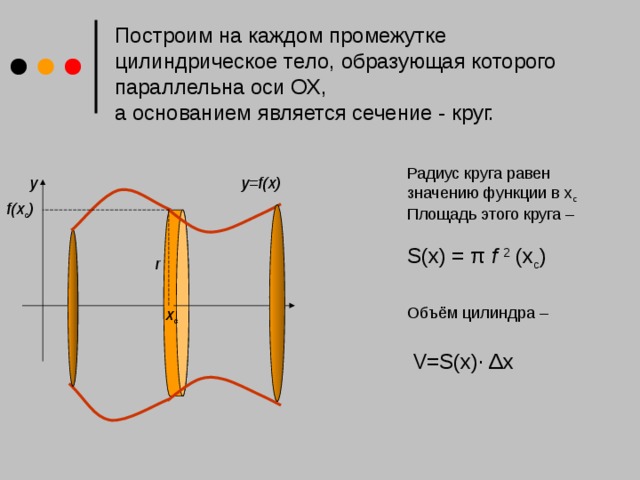
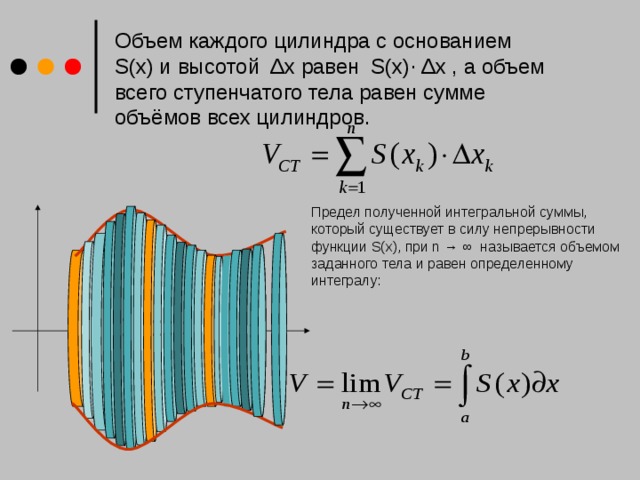
Объем каждого цилиндра с основанием S(x) и высотой Δx равен S(x) ∙ Δx , а объем всего ступенчатого тела равен сумме объёмов всех цилиндров.

Предел полученной интегральной суммы, который существует в силу непрерывности функции S(x), при n → ∞ называется объемом заданного тела и равен определенному интегралу:

Предел полученной интегральной суммы, при n → ∞ равен определенному интегралу:

Тогда объем тела вращения вокруг оси ОХ:
Если тело образовано вращением криволинейной трапеции, образованной функцией у= f(x) на отрезке [a;b],вокруг оси ОХ, то его объём можно найти по формуле:

y=f(x)

Задача.

Пусть тело образовано вращением параболы у=х 2 на отрезке [0;2] вокруг оси ОХ.

Найдите объём тела вращения.

у=х 2

Задача.

Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг оси ОХ.

Найдите объём тела вращения.

Рассмотрим конус и найдём его объём

Рассмотрим усечённый конус и найдём его объём

*** Найдите объём тела, если его поверхность получена вращением фигуры образованной графиками функций:

Вычисление определённых интегралов

Предмет: Математика

Категория: Тесты

Целевая аудитория: 10 класс.
Урок соответствует ФГОС

Скачать
Тесты по стереометрии

Автор: Тихонова Надежда Викторовна

Дата: 07.12.2017

Номер свидетельства: 442798

Похожие файлы

Создание теста по геометрии в 10 классе «Аксиомы стереометрии» в сервисе Simpoll

object(ArrayObject)#863 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(142) "Создание теста по геометрии в 10 классе «Аксиомы стереометрии»  в сервисе Simpoll "
    ["seo_title"] => string(89) "sozdaniie-tiesta-po-ghieomietrii-v-10-klassie-aksiomy-stierieomietrii-v-siervisie-simpoll"
    ["file_id"] => string(6) "140698"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1417984389"
  }
}

Презентация по математике "Уроки стереометрии"

object(ArrayObject)#885 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(87) "Презентация по математике "Уроки стереометрии" "
    ["seo_title"] => string(53) "priezientatsiia-po-matiematikie-uroki-stierieomietrii"
    ["file_id"] => string(6) "170798"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1423586554"
  }
}

Тест по теме "Аксиомы стереометрии и следствия из них"

object(ArrayObject)#863 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(99) "Тест по теме "Аксиомы стереометрии и следствия из них" "
    ["seo_title"] => string(61) "tiest-po-tiemie-aksiomy-stierieomietrii-i-sliedstviia-iz-nikh"
    ["file_id"] => string(6) "190708"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "testi"
    ["date"] => string(10) "1427211511"
  }
}

Тест по темам : «Аксиомы стереометрии и их следствия» , «Параллельность прямой и плоскости»

object(ArrayObject)#885 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(167) "Тест по темам : «Аксиомы стереометрии и их следствия» , «Параллельность прямой и плоскости»"
    ["seo_title"] => string(80) "tiest_po_tiemam_aksiomy_stierieomietrii_i_ikh_sliedstviia_paralliel_nost_priamoi"
    ["file_id"] => string(6) "428154"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "testi"
    ["date"] => string(10) "1505387289"
  }
}

Тесты по стереометрии

object(ArrayObject)#863 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(40) "Тесты по стереометрии"
    ["seo_title"] => string(21) "testy_po_stereometrii"
    ["file_id"] => string(6) "519105"
    ["category_seo"] => string(9) "geometria"
    ["subcategory_seo"] => string(5) "testi"
    ["date"] => string(10) "1567670267"
  }
}

Тесты по стереометрии

Просмотр содержимого документа «Тесты по стереометрии»

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Тесты по стереометрии»