| № | Вариант 1 |
| 1 часть |
|
1. | Вычислите 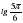
1) 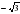 ; 2)1; 3) ; 2)1; 3) 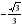 ; 4) -1 ; 4) -1 |
| 2. | Решите уравнение 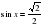
1) 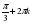 , k , k  Z, Z, 2) 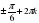 , k , k  Z, Z, 3) 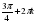 , k , k  Z , Z ,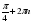 , n , n Z, Z,
4) 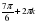 , , 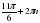 , , 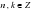 |
| 3. | Решите неравенство 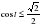 1) 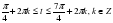 2) 2) 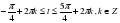
3) 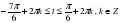 4) 4)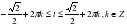 |
| 4. | Упростите выражение 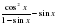 1)sin2x 2) cos2x 3) 1 4) 0 |
| 5. | Найдите значение функции: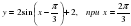 1) 3 2)  3) 2 3) 2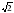 4) 5 4) 5 |
| 6. | Вычислите: cos 4050 – sin 6600 – tg 1500 1) 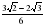 2) 2) 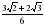 3) 3) 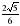 4) -2 4) -2 |
| 7. | Найдите значение sin1200 1) 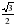 2) 2) 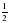 3) - 3) - 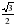 4) - 4) -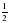 |
| 8. | Упростите выражение: 12+7sin2х+7cos2х
1) 12 2) 7 3) 26 4) 19 |
| 9. | Решите уравнение cos х=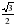 1) ± 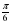 +2πп, пϵZ 2) ± +2πп, пϵZ 2) ± 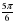 +2πп, пϵZ 3) ± +2πп, пϵZ 3) ± 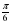 +πп, пϵZ 4) ± +πп, пϵZ 4) ± 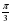 +2πп, пϵZ +2πп, пϵZ
|
| 10. | Укажите, на каком рисунке изображен график функции у= sinх. 1) 2)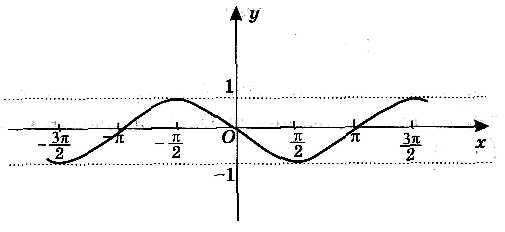 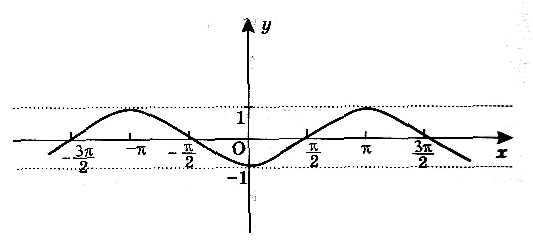
3) 4)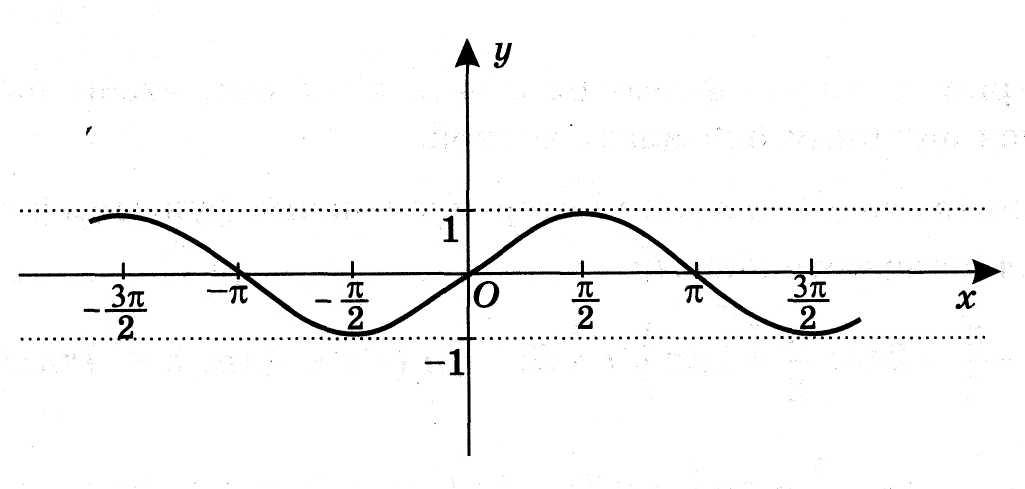 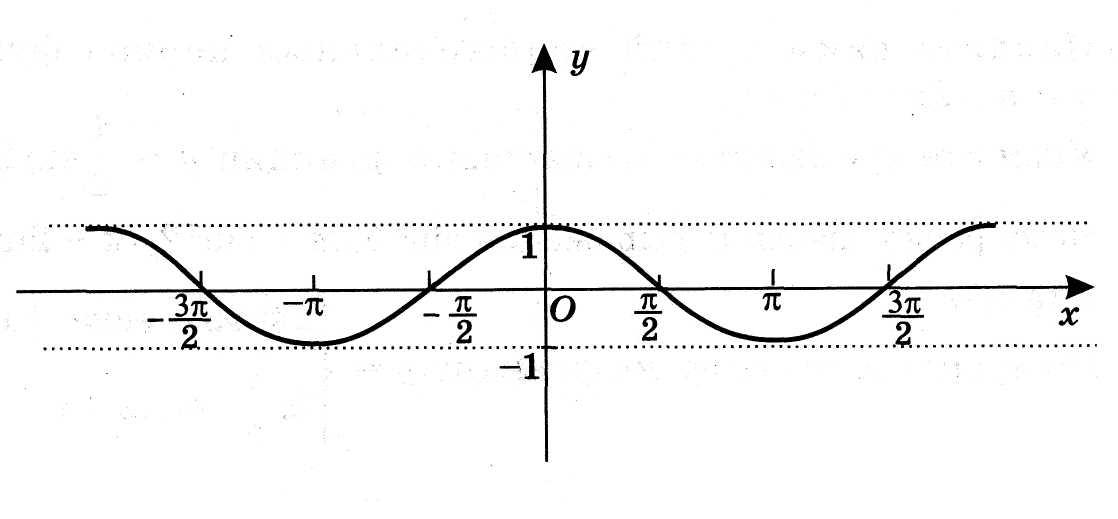
|
| 11. | Вычислите: sin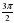 + tg + tg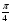 - cos - cos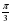
а) 1,5 б) - 0,5 в) 0,5 г) 1 |
| 12. | Вычислите: arccos( -  ) – arctg1 + arcsin0 ) – arctg1 + arcsin0 а) 0 б) -1 в) π г) 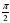 |
| 13. | Найдите множество значений функции у= cosх – 3
а) [-1;1] б) [- ∞; + ∞] в) [- 4;- 2] г) [2;4] |
| II часть |
| 1. | Известно, что cost = - 0,8, где  . Найдите tgt . Найдите tgt |
| 2. | Решите уравнение: │х-4│+│2х-3│=35 |
| 3. | Найти область определения функции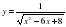 |
| 4. | Построить график функции у=3sin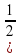 x- x-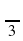 ) ) |
| 5. | Упростите выражение: 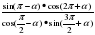 . .
|
| 6. | Найдите сtgα, если sinα = -  , π˂ α ˂ , π˂ α ˂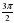 . . |
| 7. | Решите уравнение tg( ) = - ) = - |
| 8. | Отрезок АВ не пересекает плоскость  , точка С – середина отрезка АВ. Через точки А, В, С проведены параллельные прямые, пересекающие , точка С – середина отрезка АВ. Через точки А, В, С проведены параллельные прямые, пересекающие  в точках в точках  .Найти .Найти  ,если ,если  =17см, =17см,  =24см. =24см. |
| 9. | Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке М, а сторону BC - в точке N. Найдите длину отрезка MN , если АВ=15, АМ : AC=2 : 3. |
| 10. | В треугольнике угол АВС угол С равен 90°, угол А равен 30°, АС= . Найдите ВС. . Найдите ВС. |
| III часть |
| 1. | Найдите корни уравнения 2cos2х – cosх – 3 = 0, принадлежащие отрезку [ - 3π; 3π] . |
| 2. | Решить уравнение   |
| 3. | Через точку К, лежащую между параллельными плоскостями  , проведены прямые a и b. Первая прямая пересекает плоскости , проведены прямые a и b. Первая прямая пересекает плоскости  в точках в точках  и и  соответственно, вторая- в точках соответственно, вторая- в точках  и и  . Вычислите длину отрезка К . Вычислите длину отрезка К , если , если  : :  =3:5, =3:5,  =16 см. =16 см. |
| № | Вариант 2 |
| 1 часть |
| 1. | Вычислите 
1) 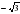 ; 2)1; 3) ; 2)1; 3) 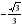 ; 4) -1 ; 4) -1 |
| 2. | Решите уравнение 
1) 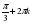 , k , k  Z, Z,
2) 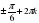 , k , k  Z, Z,
3) 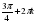 , k , k  Z , Z ,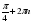 , n , n Z, Z,
4) 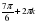 , , 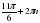 , , 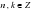 |
| 3. | Решите неравенство 
1) 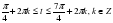 2) 2) 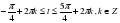
3) 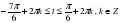 4) 4)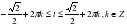 |
| 4. | Упростите выражение  1) sin2x 2) cos2x 3) 1 4) 0 |
| 5. | Найдите значение функции: 1)  2) 2)  3) - 3) -  4) - 4) - 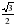 |
| 6.
| Вычислите: 1) 0 2) 1 3) – 1 4) 2
|
| 7. | Найдите значение cos1500 а) 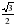 б) б)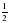 в) - в) - 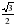 г) - г) -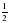 |
| 8. | Упростите выражение: 15+3sin2х+3cos2х
А) 18 б) 15 в) 19 г) 21 |
| 9. | Решите уравнение sinх= а) (-1)п  +πп, пϵZ б) (-1)п +πп, пϵZ б) (-1)п 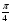 +πп, пϵZ в) ± +πп, пϵZ в) ± 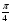 +2πп, пϵZ г) (-1)п +2πп, пϵZ г) (-1)п 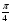 +2πп, пϵZ +2πп, пϵZ |
| 10. | Укажите, на каком рисунке изображен график функции у=cosх. а) б) 
в) г) 
|
| 11. | Вычислите: cos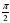 - сtg - сtg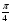 + sin + sin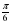 а) - 0,5 б) 1,5 в) 1 г) 0,5 |
| 12. | Вычислите: arcsin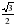 + arccos( - + arccos( - 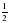 ) – arctg0 ) – arctg0 а) 1 б) 0 в) π г) - 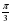 |
| 13. | Найдите множество значений функции у=sinх+2
а) [- ∞; + ∞] б) [-1;1] в) [- 3;- 1] г) [1;3] |
| II часть |
| 1. | Известно, что sint = - 0,8, где  . Найдите сtgt. . Найдите сtgt. |
| 2. | Решите уравнение: │х+10│+│2х-1│=16 |
| 3. | Найти область определения функции:  |
| 4. | Построить график функции у=1/2cos(2x+ ) ) |
| 5. | Упростите выражение:  . .
|
| 6. | Найдите tgα, если cosα = -  , , 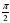 ˂ α ˂ π. ˂ α ˂ π. |
| 7. | Решите уравнение сtg( ) = 1 ) = 1 |
| 8. | Отрезок АВ не пересекает плоскость  , точка С – середина отрезка АВ. Через точки А, В, С проведены параллельные прямые, пересекающие , точка С – середина отрезка АВ. Через точки А, В, С проведены параллельные прямые, пересекающие  в точках в точках  . Найти . Найти  ,если ,если  =27см, =27см,  =16см. =16см. |
| 9. | Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке М, а сторону BC - в точке N. Найдите длину отрезка MN , если NC=10, АB : BC = 4 : 5. |
| 10. | В треугольнике угол АВС угол С равен 90°, угол А равен 30°, ВС= . Найдите АС. . Найдите АС. |
| III часть |
| 1. | Найдите корни уравнения sin2х – 6sinх +5 = 0, принадлежащие отрезку [ - 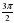 ; ;  ] . ] . |
| 2. | Найдите наибольший целый корень уравнения  |
| 3. | Луч КМ пересекает параллельные плоскости  в точках в точках  и и  , а луч КР - в точках , а луч КР - в точках  и и  соответственно. Вычислите длину отрезка соответственно. Вычислите длину отрезка  , если К , если К =8см, =8см,  : :  = 4:9. = 4:9. |
Каждое задание 1 части оценивается в 1 балл, 2 части – в 2 балла, 3 части – в 3 балла.