В данном тесте 30 вопросов по всему курсу тригонометрии. Рекомендую данную работу дать учащимся 10 класса на 2 урока. Ответы на задания выделены красным шрифтом, поэтому распечатывать, в дальнейшем, работу на цветном принтере нет смысла. Очень надеюсь на то, что многим учителям пригодится данная работа, т.к. такой способ периодической оценки знаний учащихся очень хорошо сэкономит время учителя при проверке.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Тест по тригонометрии № 1
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Тест по тригонометрии № 1 »
Полезное для учителя
Распродажа видеоуроков!
1630 руб.
2330 руб.
2100 руб.
3000 руб.
2100 руб.
3000 руб.
1970 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
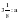 , если
, если 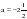
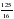
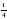
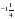
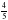
 k2
k2 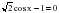
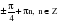
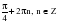
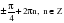
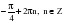
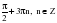
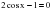
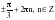
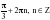
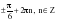
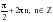
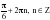
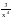 + 2
+ 2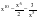
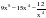
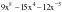
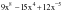
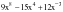
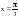
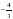
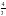
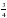
 м
м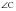 =30о,
=30о, 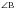 = 45о. Найти АС.
= 45о. Найти АС.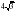
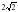
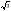
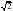
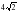
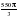 см3
см3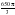 см3
см3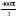 см3
см3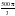 см3
см3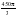 см3
см3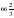 % от производительности завода А, определить, через сколько дней будет выполнен заказ.
% от производительности завода А, определить, через сколько дней будет выполнен заказ. 10
10















