Тест по теме: "Решение линейных неравенств" разработан в двух вариантах.
ТЕСТ ПО ТЕМЕ «РЕШЕНИЕ ЛИНЕЙНЫХ НЕРАВЕНСТВ» 8 КЛАСС ВАРИАНТ № 1
1. На каком из чертежей изображен числовой промежуток ( - ∞; 3]?
1)
2)
3) 4)
2. На каком из чертежей изображен числовой промежуток, соответствующий неравенству - 4 < х ≤ 5?
1) 2)
3) 4)
3. Какое из чисел является решением неравенства 3х > х + 3?
1) - 1; 2) 2; 3) 0; 4) -2.
4. Неравенству х < 5 соответствует промежуток
1) ( - ∞; 5]; 2) [5; +∞); 3) ( - ∞; 5); 4) (5; +∞).
5. Решите неравенство 3х < 18
1) ( - ∞; 6]; 2) [6; +∞); 3) (6; +∞); 4) ( - ∞; 6).
6. При каких значениях х значение выражения - 4х меньше 20?
1) ( - ∞;); 2) (; +∞); 3) ( - ∞; -5); 4) (-5; +∞).
7. Решите неравенство 3(х – 2) ≤ 6х – 4
1) [; 2) (- ∞; ; 3) (- ∞; ; 4) [ .
8. На каком чертеже изображено множество решений неравенства
-3(5 – 2х) + 5 > 4 – 2(х – 1)?
1) 2)
3) 4)
9. При каких значениях х выражение принимает неотрицательные значения?
1) [3; +∞); 2) ( - ∞; 3]; 3) [; 4) (- ∞;.
10. Решите неравенство
1) (8; +∞); 2) ( - ∞; 8]; 3) [8; +∞); 4) ( - ∞; 8).
11. Решите неравенство +
1) [12,5; +∞); 2) ( - ∞; 12,5]; 3) ( - ∞; 0,08]; 4) [0,08; +∞).
12. Укажите наибольшее целое решение неравенства 3(х – 6) – 2(х + 8) < 7
1) 41; 2) 40; 3) 1; 4) 42.
13. Укажите наименьшее целое решение неравенства
1) 1; 2) -2; 3) -1; 4) 0.
14. При каких значениях х имеет смысл выражение ?
1) ( - ∞; 4); 2) (4; +∞); 3) [4; +∞); 4) ( - ∞; 4].
15. Решите неравенство 6(3 – 2х) + 3(4х – 2) ≥ 0
1) х ≥ 0; 2) нет решений; 3) х – любое число; 4) х ≥ -12.

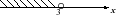
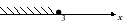 4)
4) 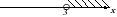
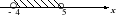 2)
2) 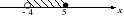
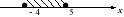 4)
4) 
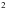 1)
1) 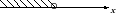 2)
2) 
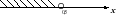 4)
4) 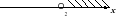
 2)
2) 
 3)
3)  4)
4) 
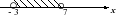 2)
2) 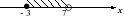
 3)
3)  4)
4) 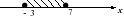
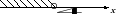 2)
2) 
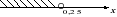 4)
4) 
















