Итоговая контрольная работа.
I вариант
1.Точки А, В, С, и D не лежат в одной
плоскости. Докажите, что прямая,
проходящая через середины отрезков DA и
DB, параллельна плоскости АВС.
2. Из точки к плоскости проведены две
наклонные. Одна из наклонных равна 10см и
имеет проекцию длиной 8см. Найдите длину
второй наклонной, если она образует с данной
плоскостью угол 30 .
.
3. SC – перпендикуляр к плоскости
прямоугольного треугольника АВС
(В = 90 ). Найдите расстояние от точки S до
). Найдите расстояние от точки S до
прямой АВ, если АС = 13см, АВ = 5см,
SC = 16см.
4. Даны координаты точки А(3;-1;2) и В(2;1;-4).
Найдите координаты точки D, если
А – середина отрезка ВD. Сравните модули
векторов 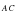 и
и 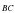 , если С(1;5;-2)
, если С(1;5;-2)
I вариант
1.Точки А, В, С, и D не лежат в одной
плоскости. Докажите, что прямая,
проходящая через середины отрезков DA и
DB, параллельна плоскости АВС.
2. Из точки к плоскости проведены две
наклонные. Одна из наклонных равна 10см и
имеет проекцию длиной 8см. Найдите длину
второй наклонной, если она образует с данной
плоскостью угол 30 .
.
3. SC – перпендикуляр к плоскости
прямоугольного треугольника АВС
(В = 90 ). Найдите расстояние от точки S до
). Найдите расстояние от точки S до
прямой АВ, если АС = 13см, АВ = 5см,
SC = 16см.
4. Даны координаты точки А(3;-1;2) и В(2;1;-4).
Найдите координаты точки D, если
А – середина отрезка ВD. Сравните модули
векторов 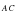 и
и 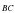 , если С(1;5;-2)
, если С(1;5;-2)
II вариант
1.Точки А, В, С, и D не лежат в одной
плоскости. Докажите, что прямая,
проходящая через середины отрезков AВ и
АС, параллельна плоскости DВС.
2. Из точки к плоскости проведены две
наклонные. Одна из наклонных равна 16см и
образует с данной плоскостью угол 30 .
.
Найдите длину второй наклонной, если ее
проекция на данную плоскость равна 6см.
3. SА – перпендикуляр к плоскости
прямоугольника АВСD. Найдите его длину,
если АВ = 5см, если ВD = 13см, а точка S
удалена от прямой СD на 15см.
4. Даны координаты точки А(3;-1;2) и В(2;1;-4).
Найдите координаты точки D, если В –
середина отрезка АD. Сравните модули
векторов 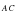 и
и 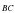 , если С(-4;3;2)
, если С(-4;3;2)
II вариант
1.Точки А, В, С, и D не лежат в одной
плоскости. Докажите, что прямая,
проходящая через середины отрезков AВ и
АС, параллельна плоскости DВС.
2. Из точки к плоскости проведены две
наклонные. Одна из наклонных равна 16см и
образует с данной плоскостью угол 30 .
.
Найдите длину второй наклонной, если ее
проекция на данную плоскость равна 6см.
3. SА – перпендикуляр к плоскости
прямоугольника АВСD. Найдите его длину,
если АВ = 5см, если ВD = 13см, а точка S
удалена от прямой СD на 15см.
4. Даны координаты точки А(3;-1;2) и В(2;1;-4).
Найдите координаты точки D, если В –
середина отрезка АD. Сравните модули
векторов 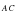 и
и 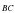 , если С(-4;3;2)
, если С(-4;3;2)
 .
.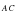 и
и 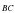 , если С(1;5;-2)
, если С(1;5;-2)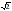 см. Найдите площадь квадрата.
см. Найдите площадь квадрата.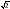 см, а прямая МВ наклонена к плоскости квадрата под углом 450. Найдите расстояние от точки М до плоскости квадрата.
см, а прямая МВ наклонена к плоскости квадрата под углом 450. Найдите расстояние от точки М до плоскости квадрата.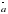 (1; -2; 4
(1; -2; 4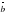 (2; 2
(2; 2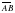 и
и 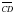 коллинеарны, если А(-2; -1; 2), В(4; -3; 6),
коллинеарны, если А(-2; -1; 2), В(4; -3; 6), 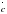 (1; 4; -3).
(1; 4; -3). 
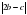 .
.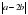 .
. , В
, В ВВ
ВВ , а сторону РК в точке К
, а сторону РК в точке К проведены две
проведены две  , а расстояние
, а расстояние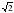 дм.
дм.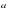 ,
,  и
и 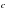 , причем:
, причем: 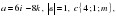
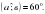
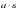 ;
;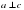 .
.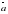 (0; 2; 1) и
(0; 2; 1) и 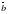 (1; 0; 2).
(1; 0; 2).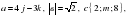
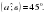 Найти:
Найти: 















