Тест
1.Вычислите √((-27)^2 )+(-4)^3+(-8)^2
А)0
В)27 +
С)75
Д)-75
Е)51
2. Вычислите √(0,04+) ?0,125-√100
А)-11,7
В)-10,3
С)-9,3 +
Д)-9,2
Е)-9,1
3. Вычислите х<0,у>0; х√у+√(х^2 )?у
А)√(2х&у)
В)1
С)0 +
Д)√(-2х&у)
Е)ху
4.Освободитесь от иррациональности в знаменатели дроби1/√(2-√3)
А)3
В)2+√3
С) √(2+√3) +
Д)√(2+√3) /3
Е) √(2-√3)
5.Найдите наименьшее значение х, если (√2?√3?√4?√5???√10)/х
А)√2
В)√6
С) √7 +
Д) √8
Е) √5
Вычислите: √(а+1/а+2) + √(а+1/а-2), если а>1.
1
A
1/(√a)
2/(√a)
2√a +
Вычислите выражение: x-√(4-√2-y),если x=√(3-√2) , y=(√8х?√(10&x^5 ))/√(3-2√2+1) .
6
√2
2√2
1 +
-6
Вычислите: √((x-2y))2 - ?(?8y?^3 )-√(x^2 ), где х<0; у>0.
1
0 +
-2х
2y
y
Сократите дробь: ((√45-√20)(√12+√75)?7√3)/(√5+√180)
10
12+
6
8
14
Упростите выражение: (1-√3)?(√(1+√3) )?(1+√3) ?√(6&1+√3)
-2+
2
4
1
1+√3
Упростите выражение: (2a-3)/√(2a+√24a+3) + (a+√3a)/√(6&a^3 )
2√a
2√a-1
2√a+1
(√2+1)√a +
√a
√((-4)^2 )-√(4^2 )- √((-9)^2 )-√(10-2√9) =?
А)-10
В)-11 +
С)-9
Д)9
Е)5
13. А=√(2х-6+2√(х^2-6х+5)-) √(2х-6-2√(х^2-6х+5).) Найдите А² , если х≥ 5
А)х-2
В)2х+4
С)4(х-5) +
Д)2х+1
Е)2х
14. Освободитесь от иррациональности в знаменатели дроби:√(6-1)/?(73-√4704) .
А)2-√6
В)1-√6
С)1+√6
Д)1 +
Е)3
15. Вычислите 1/(2-√3) - 3/√3.
А)2 +
В) √3
С)2+√3
Д)3+2√3
Е)3
16. Упростите выражение: 1+1/(1+√2) + 1/(√2+√3) + 1/(√3+√4) +???+ 1/(√97+√98).
А)6√2
В)7√2 +
С)54
Д)63
Е)8√2
17. Вычислите: х^(1/4) + х^(-1/4) + ((1-√х) (1- х^(-1/4) ))/(1+ х^(1/4) )
А) 2 +
В) х^(1/4) - √х
С) ( √х-1)/х^(1/4)
Д) (х^(1/4)- √х)/√х
Е)0
18. Упростите выражение: (?(-8)- ?((-4)^2 ))/((-1)^(-1)-2^2 )
А)-1
В)0
С)4⁄5 +
Д)1
Е)5⁄4
19. Упростите выражение:(√8? ?4? ?2)/(√(16&16)? ?2)
А)√(2&2^11 ) +
В)2√(6&36)
С)√(12&1/8)
Д)√(12&2)
Е)2
20. Упростите выражения:?(-9?√(8+3/2)) ?√(2/9??8)
А)3√3
В)- 3√3
С)1⁄2
Д)3
Е)-3 +
21. Упростите выражение:√0,001?(√(4,9 )- √0,9)
А)1⁄5
В)1⁄25 +
С) 3⁄5
Д)16⁄25
Е)4⁄25
22. Упростите выражение:(√(75-) √(48+) √108+√12):3√3
А)2
В)3 +
С)5
Д)9
Е)12
23. √(9&8)+?512+√(12&16)=?
А)√(6&2)
В)6?2
С)4^(1⁄3)
Д)2?2^(1/3)+8 +
Е)3^(1⁄3)
24. Выразите число √200 через х , если х=√(1+√50) .
А)4(х^2-1)
В)4(х+1)
С)4(х-1)
Д)2(х^2-1) +
Е)2(1-х^2)
25.Упростите выражение:(1+3/√3)/(3/√3-1) - √3
А)√3
В)2+√3
С)2-√3
Д)2 +
Е)1
Первообразная и интеграл
Дифференцируемая функция F(x) называется первообразной для функции f(x) на промежутке X, если для любого x є X справедливо равенство F’(x)=f(X). F(x) = ∫?(x)dx. Если F(x) – первообразная для функции f(x) на промежутке Х, то у функции f(x) бесконечно много первообразных, и все эти первообразные имеют вид F(x) +C, где С – произвольная постоянная. Пусть задана f(x) функция. Множество всех первообразных для f(x) называется неопределенным интегралом от f(x) и обозначается ∫?f(x)dx.Операция нахождения неопределенного интеграла по заданной функции f(x) называется интегрированием этой функции.
Свойства неопределенного интеграла
Первообразная суммы функций, равна сумме их первообразных. ∫??[(x)+g(x)]dx?=∫?f(x)dx+∫?g(x)dx
Например: ∫?(sinx+lnx)dx=∫?sinxdx+∫?lnxdx
Первообразная разности функций, равна разности их первообразных. ∫??[f(x)-g(x)]dx?=∫?f(x)dx-∫?g(x)dx
Например: ∫?(x^2-2^x )dx=∫??x^2 dx?-∫??2^x dx?
Постоянный множитель выносится перед знаком первообразной функции. ∫??a?f(x)dx?=а? ∫?f(x)dx
Например: ∫??2?x^3 dx?=2? ∫??x^3 dx?
Производная от неопределенного интеграла равна подынтегральной функции, а дифференциал – подынтегральному выражению.
d/dx ∫?f(x)dx=f(x) и d∫??f(x)dx=f(x)dx?
Например: d/dx [∫?ln?xdx ]=ln?x
Основные правила интегрирования
∫?x^n dx = x^(n+1)/(n+1)+c,n ≠ -1
Например: ∫??x^2 dx=x^(2+1)/(2+1)+c=x^3/3+c?
∫??(f’(x))/(f(x)) dx=ln|f(x) |+c?
∫??a^x dx=a^x/lna?+C
Например: ∫??6^x dx=6^x/ln6+С?
∫??e^x dx?=e^x+C
∫?sin xdx=-cosx+C
∫?cos??xdx=sin??x+C? ?
∫?1/(?cos?^2 x) dx=tgx+C
∫??1/(?sin?^2 x) dx=-ctgx+C?
∫?1/√(1-x^2 ) dx=arcsinx+c=-arcosx +C
∫?1/(1+x^2 ) dx = arctgx +c=-arcctgx+c
Неопределенный интеграл
Определенным интегралом на промежутке [а;b] от непрерывной функций y=f(x) является интеграл функции f(x) на промежутке от a до b . Здесь a и b нижний и верхний пределы интегрирования соответственно. Если функция F(x)- первообразная функции f(x) на отрезке [a;b], тогда ∫_a^b??f(x)dx=F(x)?|?(b@a)= F(b) – F(a) Эта формула называется формулой Ньютона-Лейбница.
Пример 1: ∫_1^2?x^5 =x^6/6??(2@1)=2^6/6-1^6/6=64/6-1/6=21/2
∫_0^1??e^x dx?=e^x ??(1@0)=e^1-e^0=e-1
∫_0^(π/2)?cos??xdx=sin??x??(π⁄2@0)? ? = sin??π/2?- sin??0=1-0=1?
∫_0^2??(x+?1)3dx= ((x+1)^4)/4 ??(2@0) = 3^4/4-1^4/4=20
∫_1^2?1/(2x-1) dx= ln???2x-1??/2 ??(2@1)= ln3/2-ln1/2=ln/2=ln√3
Свойства определенного интеграла
∫_a^b??[f(x)+ g(x)]dx= ? ∫_a^b??f(x)dx+ ∫_a^b?g(x)dx?
∫_a^b??k ?f(x)dx=k∫_a^b?f(x)dx?
∫_a^b??(x)? dx=∫_a^c??(x)? dx+∫_c^b??(x)? dx,
C є [a;b]
∫_a^b??f(x)? dx=-∫_b^a?f(x)dx
∫_a^a??f(x)? dx=0
Пример 2:
∫_0^(π⁄3)??(cos??x-sin??x)? ? ? dx= ∫_0^(π⁄3)?cos??xdx- ? ∫_0^(π⁄3)?sin?xdx =(sin??x+cos??x)? ???(π⁄3@0)= ?(sin???π/3+cos??π/3)? ? - (sin??0+ cos?0 ?)= (√3-1)/2
Тест
Вычислите:∫?sin?2х dх.
sin2x+c
1/2sin2x+c
1/2 cos2x+c
-1/2 cos2x+c +
-1/2 sin2x+c
2. Вычислите: ∫??(х+1)^21 ? dх.
А) ((x+?1)?^22)/22+c +
В) ((x+?1)?^20)/20+c
С) 21(x+?1)?^20+c
D) ((x+?1)?^20)/22+c
Е) ((x+?1)?^21)/22+c
3. Вычислите: ∫??(3х^2-2х+1?) dх.
А)х^3+х^2+х+с.
В) х^3+х^2-х+с.
С) х^3-х^2+х+с. +
Д) ?3х?^3-2х^2+х+с.
Е) ?3х?^3+2х^2+х+с.
4. Вычислите: ∫?sin^2 3хdх.
А)х/2+sin?6х/12+с.
В) х/2-sin?6х/12+с. +
С) х/2-cos?6х/12+с.
Д) х/2+cos?6х/12+с.
Е) х/2-sin?6х/6+с.
5. Вычислите: ∫?tg хdх.
А)-ln|cos?х|+с +
В) ln|cos?х|+с
С) -ln|sin?х|+с
Д) ln|sin?х|+с
Е)(?tg?^2 х)/2+с
6. Вычислите: ∫??[sin^х]?dх.
А) sin2x+c
В) 1/3 sin3x+c
С) 1/3 sin3x+1/3 cos3x+c
D) x+c +
Е) sin2x+cos2x+c
7. Вычислите: ∫??1/(x+5) dx?
A) ln?x+5?+c +
B) 1/5 ln?x+5?+c
C) 5ln?x+5?+c
D) 1/(x+5)
E) √(x+5)+c.
8. Вычислите:∫??(х^2 )/√(6&х^2 )dх
А)√(6&х^5 )+с
В)5/6?√(6&х^5 )+с
С) 6/5?√(6&х^5 )+с +
Д√(5&х^6 )+с
Е) - 5/6?√(6&х^5 )+с
9. Вычислите:∫?sin??(е^х ? +1)? е^хdх.
А)cos??(e^х ?+1)+с
В)- cos??(e^х ?+1)+с +
С) - sin??(e^х ?+1)+с
Д)- e^х?cos??(e^х ?+1)+с
Е)- (??e^х ?+1) cos??(e^х ?+1)+с
10.Вычислите:∫?е^(1+sinx) ?cosxdx.
E1+sinx+c. +
sinx?e1+sinx+c
cosx?e1+sinx+c
(1+sinx)?esinx+c
E1+sinx+c
11.Вычислите: ∫??√(x-1)/√x dx?
X+2√x+2
X-√(x+c)
2x-√x+c
1-1/√x+c
X-2√х+с +
12.Вычислите: ∫?(cos42x-sin42x)dx
A) 1/4 sin4x+c +
B) sin4x+c
C) 4sin4x+c
D) 1/4 cos4x+c
E) 1/2 sin2x+c
13.Найдите площадь фигуры, ограниченной линиями:
Y=x2, y=0, x=4.
512
64/3 +
256/5
64/5
256
14.Найдите площадь фигуры, ограниченной линиями: y=4+3x-x2, y=0, x=0, x=1.
A) 45/6.
B) 13/6
C) 31/6 +
D) 29/6
E) 37/6
15. Найдите площадь фигуры, ограниченной линиями: y=x3, y=0, x=1.
A) ¼ +
B) 1/3
C) 1
D) 1/2
E) 1/6
16.Найдите объем тела, полученного в результате вращении трапеции, ограниченной линиями у=2х-6, х=5, у=0 вокруг оси ОХ.
A) 4π
B) 8 π
C) 32/3 π +
D) 20π
E) 36π
17.Найдите объем тела полученного и результате вращения ограниченной линиями у=ех, х=-1, х=2 у=0 и х=0 вокруг своей оси ОХ.
A) ((e^4-e^(-1))π)/2 +
B) ((e^4+e^(-1))π)/2
C) ((e^4-e^(-1))π)/4
D) ((e^4-e^(-1))π)/4
E) ((e^4-e^(-1))π)/4
18. Вычислите: ∫_(-2)^3?(2x+3)dx
A) 12
B) 13
C ) 20 +
D) 15
E) 16
19.Вычислите: ∫_1^2?(?3x?^2-4x+1)dx
A) 6
B) 5
C) 4
D) 3
E) 2 +
20.Вычислите: ∫_10^11?dx/(x-9).
A) 2 ln 2
B) 3 ln 2
C) 4 ln 2
D) ln2 +
E) ln√2
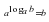 .
.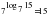 ,
, 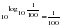 , и т.д.
, и т.д.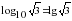 (так как основание равно 10 оно не пишется).
(так как основание равно 10 оно не пишется). 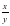
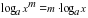
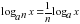
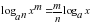
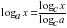
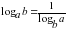
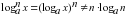
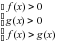 ;
;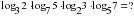
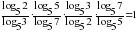
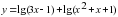
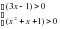 , так как
, так как 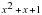 0 при любых значениях, остается 3х-10, т.е.
0 при любых значениях, остается 3х-10, т.е. 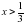 или
или 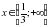
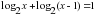
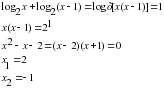
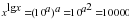
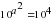

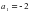 и
и 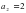
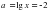 и
и 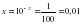
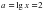 и
и 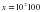
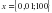

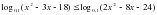
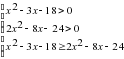

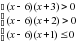
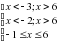
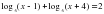 :
: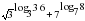
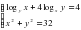
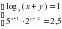
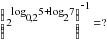
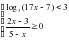
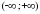
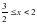 +
+















