Экзаменационная контрольная работа составлена для студентов 1 курса СПО/НПО техникумов и колледжей. Задания составлены по всем текущим темам, предусмотренных программой, с целью проведения итоговой аттестации. Данная работа может быть использована при подготовке к ЕГЭ учащихся 11 класса.Работа содержит 10 вариантов по 10 заданий в каждом варианте. На все варианты представленной контрольной работы имеются ответы, что позволит быстро проверить решения заданий.
Просмотр содержимого документа
«Экзаменационная контрольная работа »
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ЛЕНИНГРАДСКИЙ ТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
Экзаменационный материал
по математике
за II семестр
для специальности
260502 Технология продукции общественного питания
080501 Менеджмент (по отраслям)
Преподаватель:
Миргородская И.Н.
ст.Ленинградская
2010г.
Вариант № 1
Решить тригонометрическое уравнение:
а) 3 cos2 х - 4 cosх - 7 = 0
б) ctg (2х -
Решить показательное уравнение:
а)
б) 8·22x - 9·2x + 1 = 0
Решить показательное неравенство:
Решить логарифмическое уравнение:
а) log3 (1 + x) + log3 (x + 3) = 1
б) lg2 x – lg x - 6 = 0
Решить логарифмическое неравенство:
Исследовать функцию на монотонность и экстремум: f(x) = 2x3 + x2 – 3
Написать уравнение касательной к графику функции f (х)= 4х2 – 2х3 – 2х в точке с абсциссой х0 = -2.
Найти наибольшее и наименьшее значение функции f(x) = x3 - 3х + 7 на отрезке[- 3; 1].
Для функции f(x) = 2х – 3х2 + 1 найдите первообразную F ( x ), график которой проходит через точку К ( -1 ; 0 ).
Вычислите площадь фигуры, ограниченной линиями: у = - х2 + 3х; у = 0.
Вариант № 2
Решить тригонометрическое уравнение:
а) 4 sin2 х - 5sinх + 1 = 0
б) sin (3х -
Решить показательное уравнение:
а) 165 – x = 2 x + 2
б) 2·9x – 3x + 1 – 9 = 0
Решить показательное неравенство:
x - 1
Решить логарифмическое уравнение:
а) log2 (4x +3) + log2 (1 - 2x) = 1
б) log5 2 x – 2log5 x - 3 = 0
Решить логарифмическое неравенство:
Исследовать функцию на монотонность и экстремум: f(x) = - х3 + 6х2 - 4
Написать уравнение касательной к графику функции f (х) = - 4х3 + 6х2 + 5 в точке с абсциссой х0 = -1.
Найти наибольшее и наименьшее значение функции f(x) = x3 + 3х2 - 5 на отрезке [- 2; 3].
Для функции f(x) = 9x3 – 2х4 - 11 найдите первообразную F ( x ), график которой проходит через точку М(- 1 ; 18)
Вычислите площадь фигуры, ограниченной линиями: у = - х2 + х + 6; у = 0.
Вариант № 3
1. Решить тригонометрическое уравнение:
а) 3sin2 х + 5sinх = 2
б) ctg (4х -
2. Решить показательное уравнение:
а)
б) 6 ∙ 4х + 2 + 4х + 1 = 50
3. Решить показательное неравенство:
4. Решить логарифмическое уравнение:
а) lg (x – 2) + lg x = lg 8
б)log3 2 x – 3 log3 x + 2 = 0
5.Решить логарифмическое неравенство:
log4 (2x – 1) ≤ 2
Исследовать функцию на монотонность и экстремум: f(x) = 4x2 – 2x3 + 7
Написать уравнение касательной к графику функции f (х)= 2х4 – 4х + 8 в точке с абсциссой х0 = -1.
Найти наибольшее и наименьшее значение функции f(x) = x3 – 3x2 + 7
на отрезке [ 1; 3].
Для функции f(x) = 5х + х2 найдите первообразную F ( x ), график которой проходит через точку Р( - 3; 9 ).
Вычислите площадь фигуры, ограниченной линиями: у = 2х2 ; у = 0; х = 1; х = 2
Вариант № 4
Решить тригонометрическое уравнение:
а) 6sin2 х + sinх – 1 = 0
б) tg (3х +
Решить показательное уравнение:
а) 4х =
б) 72х - 8·7х + 7 = 0
Решить показательное неравенство:
271 + 2 x
Решить логарифмическое уравнение:
а) log2 (3 – x) + log2 (1 – x) = 3
б)log2 2 x – 6 log2 x = - 8
Решить логарифмическое неравенство:
Исследовать функцию на монотонность и экстремум: f(x) = 2x4 – 8x3 + 12
Написать уравнение касательной к графику функции f (х)= 7х2 – 2х3 – 12х в точке с абсциссой х0 = -1.
Найти наибольшее и наименьшее значение функции f(x) = 4x2 – x4 - 3 на отрезке [- 1; 1].
Для функции f(x) = 3 – 2х3 найдите первообразную F ( x ), график которой проходит через точку А( 1 ; 3 ).
Вычислите площадь фигуры, ограниченной линиями: у = х2 + 1; у = 0; х = 0; х = 2.
Вариант № 5
Решить тригонометрическое уравнение:
а) 2 cos2 х + 5 cosх + 2 = 0
б) 2sin(
Решить показательное уравнение:
а) 32 x – 2 = 81x
б) 22 x + 1 + 7·2x = 4
Решить показательное неравенство:
x -1
Решить логарифмическое уравнение:
а) log2 (x - 2) + log2 (x - 3) = 1
б) 2log3 2 x – 7log3 x + 3 = 0
Решить логарифмическое неравенство:
log2 (1 – 2x) ≤ 4
Исследовать функцию на монотонность и экстремум: f(x) = 7x3 + 9x2 – 3х + 6
Написать уравнение касательной к графику функции f (х)= 3х2 + 4х3 – 2 в точке с абсциссой х0 = -2.
Найти наибольшее и наименьшее значение функции f(x) = - x4 + 4х - 3 на отрезке [- 1; 1].
Для функции f(x) = - х + 1 найдите первообразную F ( x ), график которой проходит через точку В( -2 ; - 3)
Вычислите площадь фигуры, ограниченной линиями: у = х3 ; у = 0; х = - 1.
Вариант № 6
Решить тригонометрическое уравнение:
а) 3 sin2 х + sinх – 4 = 0
б) 2 cos(
Решить показательное уравнение:
а)
б) 3х+2 +4·3х + 1 = 21
Решить показательное неравенство:
x +3
Решить логарифмическое уравнение:
а) log2 (4 – x) + log2 (1 – 2x) = log2 9
б) 2log2 2 x – 5log2 x -3 = 0
Решить логарифмическое неравенство:
Исследовать функцию на монотонность и экстремум: f(x) = х3 - 12х + 2
Написать уравнение касательной к графику функции f (х)= 5х2 + 3х – 2 в точке с абсциссой х0 = 4.
Найти наибольшее и наименьшее значение функции f(x) = - x3 + 9х2 – 24х +10 на отрезке [ 0; 3 ].
Для функции f(x) = 2х + 6х2 найдите первообразную F ( x ), график которой проходит через точку N(1; 5 )
Вычислите площадь фигуры, ограниченной линиями: у = х2 + 3; у = 0; х = - 1;
х = 1;
Вариант № 7
Решить тригонометрическое уравнение:
а) 2 cos2 х + 15 cosх - 8 = 0
б) 6sin (4х -
Решить показательное уравнение:
а) 81x – 2 = 27
б) 49x - 8·7x + 7 = 0
Решить показательное неравенство:
361 – x ≤
Решить логарифмическое уравнение:
а) log5 (2x -5) + log5 (1 + x) = log5 4
б) 2log3 2 x – 3log3 x - 2 = 0
Решить логарифмическое неравенство:
log7 (x + 18) ≤ log7 8 + log7 3
Исследовать функцию на монотонность и экстремум: f(x) = 4x – х4 - 16
Написать уравнение касательной к графику функции f (х) = - 3х2 - 6х - 1в точке с абсциссой х0 =3.
Найти наибольшее и наименьшее значение функции f(x) = 3х2 – 2х3 - 4 на отрезке [ - 1; 4 ].
Для функции f(x) = 4х3 – 3х2 найдите первообразную F ( x ), график которой проходит через точку М( -1 ; 2 )
Вычислите площадь фигуры, ограниченной линиями: у = 3х2 + 3х; у = 0;
х = - 3; х = - 1.
Вариант № 8
Решить тригонометрическое уравнение:
а) 3сtg2 х + 7 сtg х - 6 = 0
б) 4cos5х - 2 = 0
Решить показательное уравнение:
а) 32х – 1 + 32х = 108
б) 4х -9·2х + 8 = 0
Решить показательное неравенство:
81x – 2 ≥
Решить логарифмическое уравнение:
а) log6 (2x - 1) + log6 (x + 5) = log6 13
б) log2 2 x – log2 x = 6
Решить логарифмическое неравенство:
log4 (x - 1) ≤ log4 8 + log4 3
Исследовать функцию на монотонность и экстремум: f(x) = 1,5х4 + 3х3
Написать уравнение касательной к графику функции f (х) = 6х– 2х3 – 2х2 в точке с абсциссой х0 = 2.
Найти наибольшее и наименьшее значение функции f(x) = 6х2 – х3 - 1 на отрезке [ - 1; 4 ].
Для функции f(x) = х – 3х2 найдите первообразную F ( x ), график которой проходит через точку А( -2; 2 )
Вычислите площадь фигуры, ограниченной линиями: у = - х2 + 2х + 3; у = 0.
Вариант № 9
Решить тригонометрическое уравнение:
а) 4 cos 2 х + 4sinх = 5
б) tg
Решить показательное уравнение:
а) 4х+1 +8·4х = 3
б) 72х - 6·7х + 5 = 0
Решить показательное неравенство:
271 + 2 x
Решить логарифмическое уравнение:
а) log2 (3 – x) + log2 (1 – x) = 3
б) 2log2 2 x – 5 log2 x - 3 = 0
Решить логарифмическое неравенство:
Исследовать функцию на монотонность и экстремум: f(x) = 0,8x5 – x4 - 8x3
Написать уравнение касательной к графику функции f (х)= 2х4 + 3х2 +3 в точке с абсциссой х0 = -2.
Найти наибольшее и наименьшее значение функции f(x) = 3x2 – x3 + 8 на отрезке[- 4; 3].
Для функции f(x) = 3x2 + 2х - 4 найдите первообразную F ( x ), график которой проходит через точку С( - 3 ; 11 ).
Вычислите площадь фигуры, ограниченной линиями: у = х2 - 4х+ 5; у = 0;
х = 1; х = 4.
Вариант № 10
Решить тригонометрическое уравнение:
а) 6 cos 2 х - 7cosх – 3 = 0
б) tg (4х +
Решить показательное уравнение:
а) 3х +2 - 5·3х = 324
б) 22х - 3·2х+1 + 8 = 0
Решить показательное неравенство:
+1
Решить логарифмическое уравнение:
а) log5 (12x+8) – log5 4 = log5 23
б) 2log3 2 x – 3 log3 x - 2= 0
Решить логарифмическое неравенство:
log4 (6x – 10) log4 24 - log4 3
Исследовать функцию на монотонность и экстремум: f(x) = - 4 - 9х + x3 – 3х2
Написать уравнение касательной к графику функции f (х)= 6х2 – х3 - 1 в точке с абсциссой х0 = -3.
Найти наибольшее и наименьшее значение функции f(x) = 2x4 – 8x + 5 на отрезке [- 3; 2].
Для функции f(x) = 4х3 - 12х + 9 найдите первообразную F ( x ), график которой проходит через точку Е(-2 ; -15).
Вычислите площадь фигуры, ограниченной линиями: у = 2х2 + 1; у = 0; х = 2; х = 3.
ОТВЕТЫ:
Вариант № 1
1
2
3
4
5
а) Х = π+2 πn, nZ
б) Х =+, nZ
а) - 3;0,5
б) 0; - 3
х (-∞;-2] [3; ∞)
а) 0
б)1000; 0,01
х [-8; )
6
7
8
9
10
f(x) возр. (-∞; -) (0; ∞)
f(x) убыв. (- ;0)
х = - т.max; х = 0 т.min
у = - 42х - 48
min f(x) = f(- 3) = -11
[-3; 1]
max f(x) = f(- 1) = 9
[-3; 1]
F(х) = х2 - х3 + х - 1
4,5 ед.кв.
Вариант № 2
1
2
3
4
5
а) Х = +2 πn, nZ
Х = (- 1)n arcsin + πn, nZ
б) Х = (- 1)n + +, nZ
а) - 5
б) 1
х ( ; + ∞)
а) - 0,5; 0,25
б)125; 0,2
х [-5,5; 2,5)
6
7
8
9
10
f(x) возр ( 0; 4)
f(x) убыв. (-∞;0) (4; ∞)
х = 4 т.max; х = 0 т.min
у = - 24х - 9
min f(x) = f( 0 ) = -5
[-2; 3]
max f(x) = f( 3) = 49
[-2; 3]
F(х) = х4 - х5 -11 х + 4
ед.кв.
Вариант № 3
1
2
3
4
5
а) Х = (- 1)n arcsin + πn, nZ
б) Х =+ , nZ
а) 2; 3
б) – 0,5
х (-∞;- 13]
а) 4
б) 3; 9
х (0,5; 8,5]
6
7
8
9
10
f(x) возр ( 0; 1)
f(x) убыв. (-∞;0) (1; ∞)
х = 1 т.max; х = 0 т.min
у = - 12х + 2
min f(x) = f( 2 ) = 3
[ 1; 3]
max f(x) = f( 3) = 7
[ 1; 3]
F(х) = х2 + х3 - 4,5
ед.кв.
Вариант № 4
1
2
3
4
5
а) Х = (- 1)n arcsin + πn, nZ
Х = (- 1)n +1 + πn, nZ
б) Х = +n, nZ
а) 2; - 3
б) 1;0
х ( - ; + ∞)
а) - 1
б) 4; 16
х ( 1; 28]
6
7
8
9
10
f(x) возр ( 3; +∞ )
f(x) убыв. (-∞;0) (0; 3)
х = 3 т.min
у = - 32х - 11
min f(x) = f( 0 ) = - 3
[ -1; 1]
max f(x) = f(- 1) = f( 1) = 0
[ -1; 1]
F(х) = 3х - х4 + 0,5
ед.кв.
Вариант № 5
1
2
3
4
5
а) Х = ± +2 πn, nZ
б) Х = (- 1)n - + πn, nZ
а) - 1
б) - 1
х (- ∞;- )
а) 4
б) 27;
х [-7,5; 0,5)
6
7
8
9
10
f(x) возр. (-∞;- 1) (; +∞)
f(x) убыв. ( - 1; )
х = т.min; х = - 1 т.max
у = 36х + 50
min f(x) = f( - 1 ) = - 8
[ -1; 1]
max f(x) = f( 1) = 0
[ -1; 1]
F(х) = - х2 + х + 1
ед.кв.
Вариант № 6
1
2
3
4
5
а) Х = +2 πn, nZ
б) Х = ± +4 πn, nZ
а) 1; 3
б) 0
х [ - 1,2 ; + ∞)
а) – 0,5
б) 8;
х ( 1; 10)
6
7
8
9
10
f(x) возр (-∞;- 2) (2; +∞)
f(x) убыв. ( - 2; 2 )
х = 2 т.min; х = - 2 т.max
у = 43х - 82
min f(x) = f( 2 ) = - 10
[ 0; 3]
max f(x) = f( 0) = 10
[ 0; 3]
F(х) = х2 + х3 + 2
ед.кв.
Вариант № 7
1
2
3
4
5
а) Х = ± +2 πn, nZ
б) Х = (- 1)n + + , nZ
а)
б) 0; 1
х [ 2 ; + ∞)
а) 3
б) 9;
х ( - 18; 6]
6
7
8
9
10
f(x) возр (-∞; 1)
f(x) убыв. ( 1; +∞)
х = 1 т.max
у = - 24х + 26
min f(x) = f( 4 ) = - 84
[- 1; 4]
max f(x) = f( -1) = 1
[- 1; 4]
F(х) = х4 – х3
14 ед.кв.
Вариант № 8
1
2
3
4
5
а) Х = π – arcctg3 + πn, nZ
Х = arcctg + πn, nZ
б) Х = ± +, nZ
а)
б) 0; 3
х [ 1 ; + ∞)
а) 1,5
б) 8; 0,25
х ( 1; 25]
6
7
8
9
10
f(x) возр (-1,5; 0) (0; + ∞)
f(x) убыв. ( - ∞; -1,5 )
х = - 1,5 т.min
у = - 26х + 40
min f(x) = f( 0 ) = - 1
[- 1; 4]
max f(x) = f( 4) = 31
[- 1; 4]
F(х) = х2 – х3 - 8
ед.кв.
Вариант № 9
1
2
3
4
5
а) Х = (- 1)n + πn, nZ
б) Х = +2 πn, nZ
а) - 1
б) 0;
х ( - ; + ∞)
а) - 1
б) 8;
х ( 1; 7]
6
7
8
9
10
f(x) возр (-∞;- 2) (3; +∞)
f(x) убыв. ( - 2; 0 ) (0; 3)
х = 3 т.min; х = - 2 т.max
у = -76х - 105
min f(x) = f( 0) = f( 3) = 8
[ - 4; 3]
max f(x) = f( - 4) = 120
[ - 4; 3]
F(х) = х3 + х2 – 4х + 17
ед.кв.
Вариант № 10
1
2
3
4
5
а) Х =±( π-arccos ) + 2πn, nZ
б) Х = - +, nZ
а) 4
б) 1; 2
х ( - ; + ∞)
а) 7
б) 9;
( 3; +∞)
6
7
8
9
10
f(x) возр (-∞;- 1) (3; +∞)
f(x) убыв. ( -1; 3)
х = 3 т.min; х = - 1 т.max
у = - 63х - 109
min f(x) = f( 1) = - 1
[ - 3; 2]
max f(x) = f( - 3) = 191
[ - 3; 2]
F(х) = х4 -6 х2 + 9х+11
ед.кв.
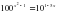
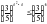
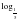 (1 – 3x) ≥ - 2
(1 – 3x) ≥ - 2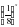 64x - 1
64x - 1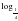 (5 – 2x) ≥ - 2
(5 – 2x) ≥ - 2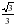

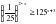
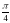 ) =
) = 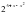
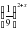
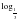 (x – 1) ≥ - 3
(x – 1) ≥ - 3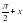 ) =
) = 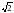
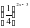
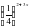 8x -1
8x -1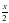 -
- 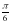 ) =
) = 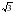
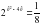
 ≤ 64x+3
≤ 64x+3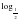 (10 – x)
(10 – x) 
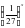
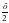 =
= 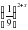
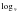 (x – 1) ≤
(x – 1) ≤  x+1
x+1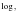 5
5















