Формирование вычислительных умений и навыков – это сложный длительный процесс, его эффективность зависит от индивидуальных особенностей ребенка, уровня его подготовки и организации вычислительной деятельности.
- Вычислительный навык – это высокая степень овладения вычислительными приемами. Вычислительные навыки рассматриваются как один из видов учебных навыков, функционирующих и формирующихся в процессе обучения.
Полноценный вычислительный навык характеризуется
- правильностью;
- осознанностью;
- рациональностью;
- обобщенность;
- автоматизмом;
- прочностью.
На современном этапе развития образования необходимо выбирать такие способы организации вычислительной деятельности школьников, которые способствуют не только формированию прочных вычислительных умении и навыков, но и всестороннему развитию личности ребенка.
Для формирования и закрепления выше перечисленных умений и навыков используются следующие приемы:
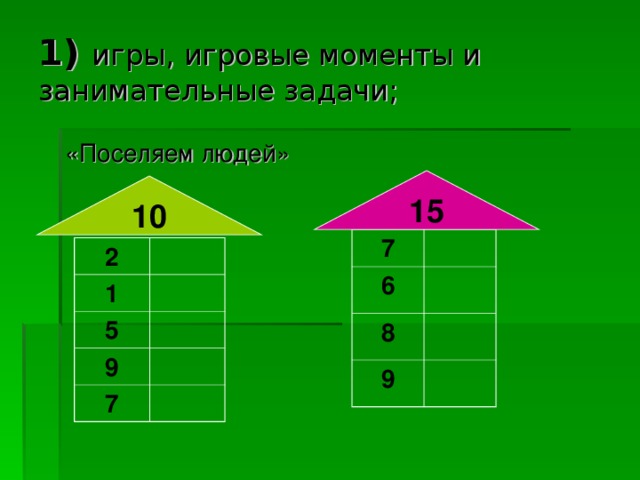
- игры, игровые моменты
- тесты «Проверь себя сам»;
- математические диктанты;
- интересные задачи
- нестандартные задачи
- занимательные задачи
- творческие задания и конкурсы;
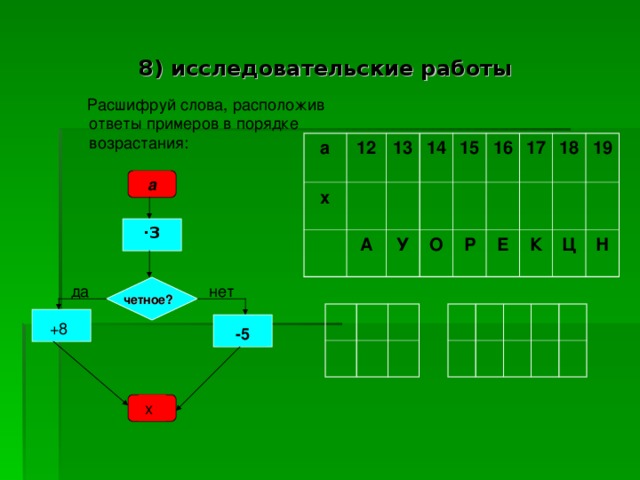
- исследовательские работы
- закономерность
Применение игр в первую очередь предназначено для того, чтобы заинтересовать наиболее пассивную часть класса, редко принимающую участие в работе на уроке при традиционном его проведении. Поэтому на начальном этапе, при введении в практику урока дидактических игр, представляет целесообразным применять игры, не требующие глубокого знания и даже понимания текущего материала. В этом случае назначение дидактических игр – в развитии познавательного интереса, способствующего накопления знаний, умений, навыков, в придании уроку более неформального характера, в привлечении внимания учащихся к проводящейся работе.
Постепенно назначение дидактических игр изменяется. Они начинают применяться для проверки полуученых знаний посредством решения не стандартных задач в привлекательной, интересной для детей форме. При этом во время игры в группе главным действующим лицом на уроке становятся сами дети, а не учителя.
При выборе способов организации вычислительной деятельности необходимо ориентироваться на развивающийся характер работы, отдавать предпочтение обучающим заданиям. Используемые вычислительные задания должны характеризоваться вариативностью формулировок, неоднозначностью решений, выявлением различных моделей (предметных, графических, символических), что позволяет учитывать индивидуальные особенности ребенка, его жизненный опыт, предметно- действенное и наглядно- образное мышление и постепенно вводить ребенка в мир математических понятий, терминов и символов.
Устные вычисления имеют большое образовательное, воспитательное и практическое и чисто методическое значение. Помимо того практического значения, которое имеет для каждого человека, умение быстро и правильно произвести несложные вычисления «в уме», устный счет всегда рассматривался методистами как одно из лучших средств углубления приобретаемых детьми на уроках математики теоретических знаний.
Упражнениям в устном счете всегда придавалось также воспитательное значение: считалось, что они способствуют развитию у детей находчивости, сообразительности, внимания, развитию памяти детей, активности, быстроты, гибкости и самостоятельности мышления.
Устные вычисления развивают логическое мышление учащихся, творческие начала и волевые качества, наблюдательность и математическую зоркость, способствуют развитию речи учащихся, если с самого начала обучения вводить в тексты заданий и использовать при обсуждении упражнений математические термины.
Вычислительные навыки формируются у учащихся на всех этапах изучения курса математики, но основа ее закладывается в первые 5-6 лет обучения. В этот период школьники обучаются именно умению осознано использовать законы математических действий (сложение, вычитание, умножение, деление, возведение в степень). В последующие годы полученные умения и навыки совершенствуются и закрепляются в процессе изучения алгебры, физики, черчении и других предметов.
В связи с этим хочется сказать, что проблема преемственности очень актуальна. И те вычислительные навыки, которые дети отрабатывают в начальном звене, должны продолжать отрабатывать и в среднем, а затем и в старшем звене.
Поэтому учителя математики, начиная со 2 полугодия, начинают посещать 4 классы.
И выявлять чем и как владеют дети, чтобы продолжить данную работу в 5 классе.
Формирование вычислительных умений и навыков – это сложный длительный процесс, его эффективность зависит от индивидуальных особенностей ребенка, уровня его подготовки и организации вычислительной деятельности.
- Вычислительный навык – это высокая степень овладения вычислительными приемами. Вычислительные навыки рассматриваются как один из видов учебных навыков, функционирующих и формирующихся в процессе обучения.
Полноценный вычислительный навык характеризуется
- правильностью;
- осознанностью;
- рациональностью;
- обобщенность;
- автоматизмом;
- прочностью.
На современном этапе развития образования необходимо выбирать такие способы организации вычислительной деятельности школьников, которые способствуют не только формированию прочных вычислительных умении и навыков, но и всестороннему развитию личности ребенка.
Для формирования и закрепления выше перечисленных умений и навыков используются следующие приемы:
- игры, игровые моменты
- тесты «Проверь себя сам»;
- математические диктанты;
- интересные задачи
- нестандартные задачи
- занимательные задачи
- творческие задания и конкурсы;
- исследовательские работы
- закономерность
Применение игр в первую очередь предназначено для того, чтобы заинтересовать наиболее пассивную часть класса, редко принимающую участие в работе на уроке при традиционном его проведении. Поэтому на начальном этапе, при введении в практику урока дидактических игр, представляет целесообразным применять игры, не требующие глубокого знания и даже понимания текущего материала. В этом случае назначение дидактических игр – в развитии познавательного интереса, способствующего накопления знаний, умений, навыков, в придании уроку более неформального характера, в привлечении внимания учащихся к проводящейся работе.
Постепенно назначение дидактических игр изменяется. Они начинают применяться для проверки полуученых знаний посредством решения не стандартных задач в привлекательной, интересной для детей форме. При этом во время игры в группе главным действующим лицом на уроке становятся сами дети, а не учителя.
При выборе способов организации вычислительной деятельности необходимо ориентироваться на развивающийся характер работы, отдавать предпочтение обучающим заданиям. Используемые вычислительные задания должны характеризоваться вариативностью формулировок, неоднозначностью решений, выявлением различных моделей (предметных, графических, символических), что позволяет учитывать индивидуальные особенности ребенка, его жизненный опыт, предметно- действенное и наглядно- образное мышление и постепенно вводить ребенка в мир математических понятий, терминов и символов.
Устные вычисления имеют большое образовательное, воспитательное и практическое и чисто методическое значение. Помимо того практического значения, которое имеет для каждого человека, умение быстро и правильно произвести несложные вычисления «в уме», устный счет всегда рассматривался методистами как одно из лучших средств углубления приобретаемых детьми на уроках математики теоретических знаний.
Упражнениям в устном счете всегда придавалось также воспитательное значение: считалось, что они способствуют развитию у детей находчивости, сообразительности, внимания, развитию памяти детей, активности, быстроты, гибкости и самостоятельности мышления.
Устные вычисления развивают логическое мышление учащихся, творческие начала и волевые качества, наблюдательность и математическую зоркость, способствуют развитию речи учащихся, если с самого начала обучения вводить в тексты заданий и использовать при обсуждении упражнений математические термины.
Вычислительные навыки формируются у учащихся на всех этапах изучения курса математики, но основа ее закладывается в первые 5-6 лет обучения. В этот период школьники обучаются именно умению осознано использовать законы математических действий (сложение, вычитание, умножение, деление, возведение в степень). В последующие годы полученные умения и навыки совершенствуются и закрепляются в процессе изучения алгебры, физики, черчении и других предметов.
В связи с этим хочется сказать, что проблема преемственности очень актуальна. И те вычислительные навыки, которые дети отрабатывают в начальном звене, должны продолжать отрабатывать и в среднем, а затем и в старшем звене.
Поэтому учителя математики, начиная со 2 полугодия, начинают посещать 4 классы.
И выявлять чем и как владеют дети, чтобы продолжить данную работу в 5 классе.
Формирование вычислительных умений и навыков – это сложный длительный процесс, его эффективность зависит от индивидуальных особенностей ребенка, уровня его подготовки и организации вычислительной деятельности.
- Вычислительный навык – это высокая степень овладения вычислительными приемами. Вычислительные навыки рассматриваются как один из видов учебных навыков, функционирующих и формирующихся в процессе обучения.
Полноценный вычислительный навык характеризуется
- правильностью;
- осознанностью;
- рациональностью;
- обобщенность;
- автоматизмом;
- прочностью.
На современном этапе развития образования необходимо выбирать такие способы организации вычислительной деятельности школьников, которые способствуют не только формированию прочных вычислительных умении и навыков, но и всестороннему развитию личности ребенка.
Для формирования и закрепления выше перечисленных умений и навыков используются следующие приемы:
- игры, игровые моменты
- тесты «Проверь себя сам»;
- математические диктанты;
- интересные задачи
- нестандартные задачи
- занимательные задачи
- творческие задания и конкурсы;
- исследовательские работы
- закономерность
Применение игр в первую очередь предназначено для того, чтобы заинтересовать наиболее пассивную часть класса, редко принимающую участие в работе на уроке при традиционном его проведении. Поэтому на начальном этапе, при введении в практику урока дидактических игр, представляет целесообразным применять игры, не требующие глубокого знания и даже понимания текущего материала. В этом случае назначение дидактических игр – в развитии познавательного интереса, способствующего накопления знаний, умений, навыков, в придании уроку более неформального характера, в привлечении внимания учащихся к проводящейся работе.
Постепенно назначение дидактических игр изменяется. Они начинают применяться для проверки полуученых знаний посредством решения не стандартных задач в привлекательной, интересной для детей форме. При этом во время игры в группе главным действующим лицом на уроке становятся сами дети, а не учителя.
При выборе способов организации вычислительной деятельности необходимо ориентироваться на развивающийся характер работы, отдавать предпочтение обучающим заданиям. Используемые вычислительные задания должны характеризоваться вариативностью формулировок, неоднозначностью решений, выявлением различных моделей (предметных, графических, символических), что позволяет учитывать индивидуальные особенности ребенка, его жизненный опыт, предметно- действенное и наглядно- образное мышление и постепенно вводить ребенка в мир математических понятий, терминов и символов.
Устные вычисления имеют большое образовательное, воспитательное и практическое и чисто методическое значение. Помимо того практического значения, которое имеет для каждого человека, умение быстро и правильно произвести несложные вычисления «в уме», устный счет всегда рассматривался методистами как одно из лучших средств углубления приобретаемых детьми на уроках математики теоретических знаний.
Упражнениям в устном счете всегда придавалось также воспитательное значение: считалось, что они способствуют развитию у детей находчивости, сообразительности, внимания, развитию памяти детей, активности, быстроты, гибкости и самостоятельности мышления.
Устные вычисления развивают логическое мышление учащихся, творческие начала и волевые качества, наблюдательность и математическую зоркость, способствуют развитию речи учащихся, если с самого начала обучения вводить в тексты заданий и использовать при обсуждении упражнений математические термины.
Вычислительные навыки формируются у учащихся на всех этапах изучения курса математики, но основа ее закладывается в первые 5-6 лет обучения. В этот период школьники обучаются именно умению осознано использовать законы математических действий (сложение, вычитание, умножение, деление, возведение в степень). В последующие годы полученные умения и навыки совершенствуются и закрепляются в процессе изучения алгебры, физики, черчении и других предметов.
В связи с этим хочется сказать, что проблема преемственности очень актуальна. И те вычислительные навыки, которые дети отрабатывают в начальном звене, должны продолжать отрабатывать и в среднем, а затем и в старшем звене.
Поэтому учителя математики, начиная со 2 полугодия, начинают посещать 4 классы.
И выявлять чем и как владеют дети, чтобы продолжить данную работу в 5 классе.