Развитие вычислительных навыков учащихся
Здравствуйте уважаемы коллеги. Свое выступление на тему развитие вычислительных навыков учащихся я хочу начать высказыванием Д. Пойа
Умение решать задачи – такое же искусство
такое же искусство, как умение плавать
или бегать на лыжах.
Ему можно научится только путем упражнения
Одним из путей таких упражнений является устный счет.
Одной из основных задач преподавания курса математики в школе является формирование сознательных и прочных вычислительных навыков у учащихся. Не секрет, что у школьников с прочными вычислительными навыками бывает гораздо меньше проблем с математикой.
Обучение в 5 классе затрудняется тем, что каждому ребенку необходимо приспособиться к новым учителям, новым предметам и новым уровням требований. Многое зависит от того, как поставит работу учитель, насколько удастся ему создать безболезненный адаптационный период, насколько он увлечет их своим предметом.
Особенно много трудностей возникает у учащихся, не владеющих навыками устного счета. Бывает так, что часть учеников в начале 5 - го класса не знают таблицу умножения, не могут выполнить простые вычисления, имеют смутное представление о порядке выполнения действий.
Поэтому учителю математики надо обратить внимание на устный счет с того момента, когда учащиеся переходят к нему из начальной школы.
Успех в вычислениях во многом определяется степенью отработки навыков устного счета.
Устные упражнения в методическом отношении представляют собой большую ценность. Они используются как подготовительный этап при объяснении нового материала, как иллюстрация изучаемых правил, законов, а также для закрепления и повторения изученного.
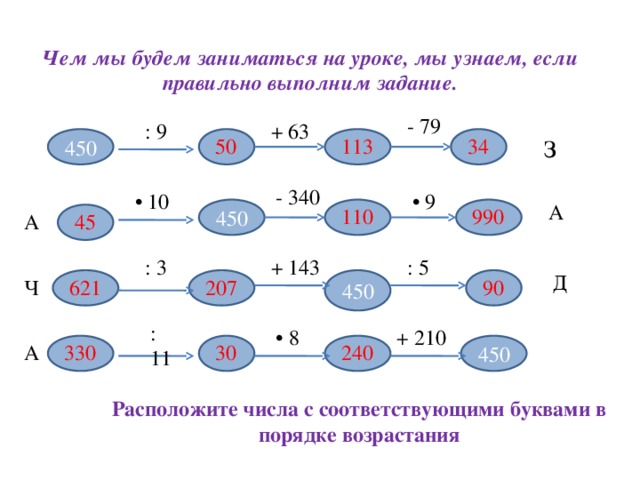
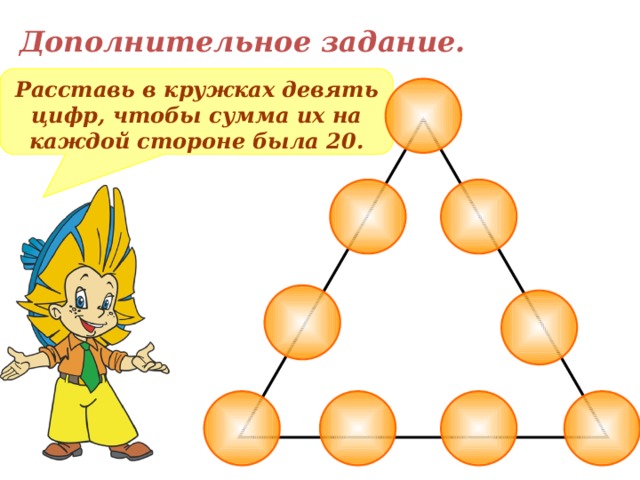
слайд 2 Пример: 1. Чем мы будем заниматься на уроке, мы узнаем, если правильно выполним задание. Зашифрованное слово (тема урока)
слайд 3 Выполнить деление :
45 : 9 ; 0 : 67; 234 : 1;
567 : 567; 34 :17; а:а;
в:0; x:x; 0:а; с:1;
47 : 13 (выход на тему деление с остатком) слайд 4
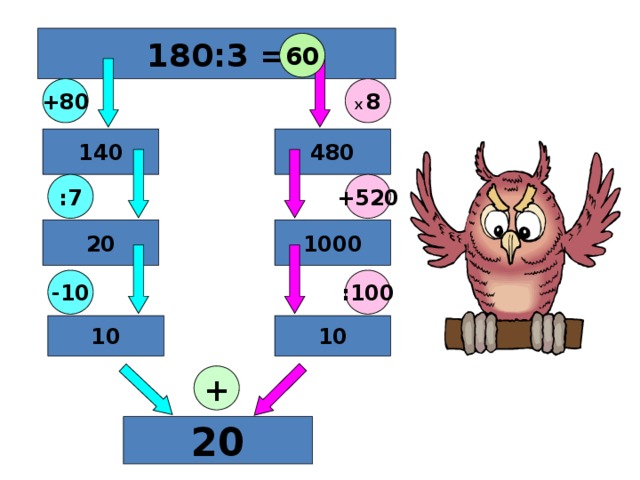
слайд 4 2. Вычисли удобным способом:
В устном счете развивается память, внимание, быстрота реакции, воспитывается умение сосредоточиться, потребность к самоконтролю, повышается культура вычислений.
Вычислительная культура формируется на всех этапах изучения курса математики. Но основа ее закладывается в первые 5-6 лет обучения. В этот период школьники обучаются именно умению осознанно использовать законы математических действий (сложение, вычитание, возведение в степень, умножение, деление. В последующие годы, полученные умения и навыки совершенствуются и закрепляются в процессе изучения математики, физики, химии и других предметов.
Вычислительные навыки и умения можно считать сформированными только тогда, когда учащиеся умеют с достаточной беглостью выполнять математические действия с натуральными числами, десятичными или обыкновенными дробями, рациональными числами, а также производить тождественные преобразования различных числовых выражений и приближенные вычисления.
О наличии у учащихся вычислительной культуры можно судить по их умению производить устные и письменные вычисления, рационально организовывать ход вычислений, убеждать в правильности полученных результатов.
В зависимости от сложности задания на практике используется три вида вычислений: письменное, устное и письменное с промежуточными устными вычислениями.
Качество вычислительных умений определяется знанием правил и алгоритмов вычислений. Поэтому степень овладения вычислительными умениями зависит от четкости сформулированного правила и от понимания принципа его использования. Умение формулируется в процессе выполнения целенаправленной системы упражнений. Очень важно владеть некоторыми вычислительными умениями до навыка.
Вычислительные навыки отличаются от умений тем, что выполняются почти бесконтрольно. Такая степень овладения умениями достигается в условиях их целенаправленного формирования. Образование вычислительных навыков ускоряется, если учащемуся понятен процесс вычислений и его особенности.
Как в письменных, так и в устных вычислениях используются разнообразные правила и приемы.
Примеры интересных приемов устного счета.
слайд 5 Пример: 23 12=276
12=276
а) 2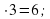 б)2
б)2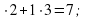 в)1
в)1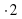 =2
=2
слайд 6 Пример: Некоторые числа можно умножать на 15 устно
42∙15 = 42∙ (10 + 5) = 420 + 210 = 630. Видно, что результат можно было получить, приписав к числу 42 справа нуль и прибавив половину полученного числа. Пользуясь этим приемом, выполните умножение на 15 чисел
а) 62; б) 120; в) 32; г) 780
У учащихся 5-го класса необходимо закреплять умение выполнять все арифметические действия с натуральными (многозначными) числами. В результате прохождения программного материала пятиклассники должны уметь выполнять основные действия с десятичными дробями; применять законы сложения и умножения к упрощению выражений; использовать признаки делимости на 10, 2, 5 и 3; округлять числа до любого разряда; определять порядок действий при вычислении значения выражения.
Пример:
слайд 7 Найдите ошибки в решении примера(порядок действия)
Успех в вычислениях во многом определяется степенью отработки у учащихся навыков устного счета. Организация устных вычислений представляет собой большую ценность. Устные упражнения используются как подготовительная ступень при объяснении нового материала, как иллюстрация изучаемых правил, законов, а также для закрепления и повторения изученного. В устном счете развивается память учащихся, быстрота реакции, воспитывается умение сосредоточиться, наблюдать, проявляется инициатива учащихся, потребность к самоконтролю, повышается культура вычислений.
При подготовке к уроку отбирается материал, систематизируется, продумывается переход от одного упражнения к другому. При продумывании системы заданий и форм организации устного счета не исключается учет индивидуальной подготовки учащихся, склонностей и способностей к устным вычислениям.
слайд 8 Например, первое время на уроках учащимся для устного счета предлагаются обычные карточки типа: (счет на время).
После того как учащиеся стали достаточно бегло считать, необходимо расширять приемы устного счета, поэтому учащимся предлагаются карточки типа 16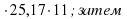 на применение законов сложения и вычитания:
на применение законов сложения и вычитания:
слайд 9 137-(37+18), 284-(84+37); 137-(37-18), (245-38)-145. Слайд
Учитель должен иметь представление об уровне вычислительных умений и навыков учащихся, сформированных ранее. Чему способствуют проведение самостоятельных работ и наблюдения за работой учащихся в классе. Анализ письменных и устных работ учащихся дает возможность установить, как усвоен данный материал, какие общие и характерные ошибки допущены при проведении вычислений, кто из учащихся и что именно не усвоил и как ликвидировать выявленные пробелы.
В ходе изучения математики учащиеся должны приобретать опыт рационального выполнения вычислений. Основой тождественных преобразований является использование законов арифметических действий. Например, при изучении темы «Применение распределительного свойства умножения» учащиеся сами делают вывод о том, что этот закон намного облегчает вычисления:
слайд 10 Применение распределительного свойства:
объясните, как выполнено умножение и вычислите:
35 ∙ 6 = (30 + 5) ∙ 6 = 30 ∙ 6 + 5 ∙ 6 =
125 ∙ 5 = (100 + 20 + 5) ∙ 5 = 100 ∙ 5 + 20 ∙ 5 + 5 ∙ 5 =
Вычислите, вынося общий множитель за скобки:
а) 90 ∙ 25 + 10 ∙ 25
б) 50 ∙ 32 – 49 ∙ 32
в) 4 ∙ 16 + 16 ∙ 6
г) 134 ∙ 25 – 34 ∙ 25
6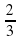
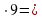 (6+
(6+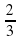 )
)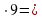 6
6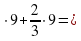 54+6=60.
54+6=60.
Представляю вам некоторые задания, которые я использую на уроках
Уравнения
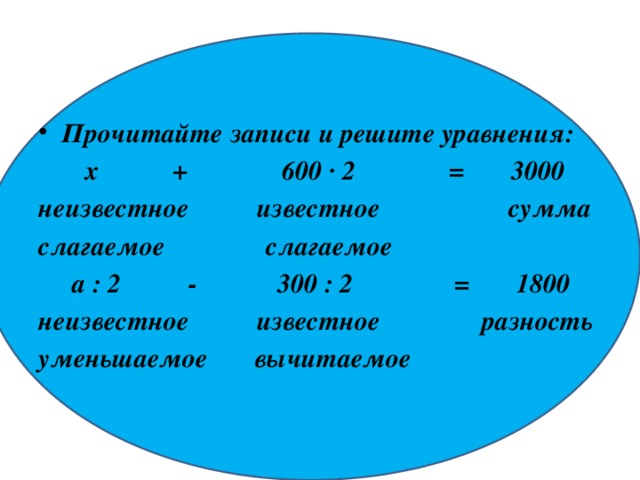
Прочитайте записи и решите уравнения:
х + 600 ∙ 2 = 3000
неизвестное известное сумма
слагаемое слагаемое
Обсудить выражения и их значения и обнаружить ошибки, если таковые имеются.
21,6+4,7=25,3;
6,7-3,9=2,8;
8,2+1,91=9,11;
5,84-2,7=3,16;
8-3,8=5,2;
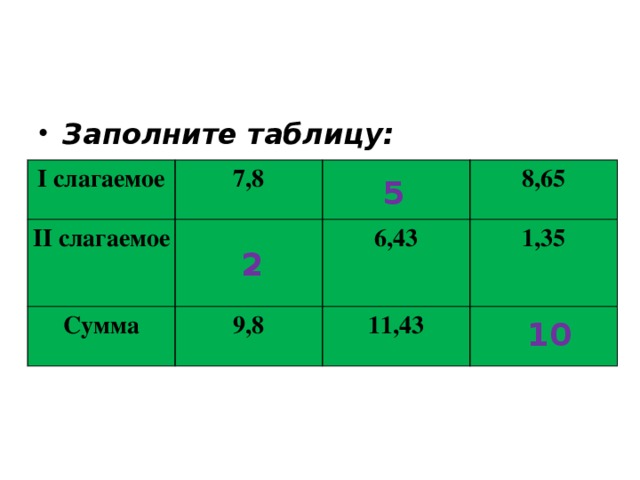
Заполните таблицу:
| I слагаемое | 7,8 |
| 8,65 |
| II слагаемое |
| 6,43 | 1,35 |
| Сумма | 9,8 | 11,43 |
|
«Найди ошибку»:
0,01·3=0,3; 0,05·2=0,01;
0,08·4=32; 0,006·3=0,18;
0,007·3=2,1; 0,01·48=0,48.
6. Вычислите
а) сумму чисел 1111 и 999
б) разность чисел 2300 и 800
в) произведение чисел 42 и 11
г) частное чисел 1890 и 9
д) разность квадратов 4 и 2
8. Математический фокус:
Задумайте число.
Прибавьте к нему 12,
Затем вычтите 7.
К результату прибавьте 8.
Скажите, сколько получилось.
Учащимся следует напоминать о том, что скорость и точность вычисления зависят от того, как ведется оформление вычислительных работ на бумаге, - письменные вычисления являются основным видом вычислительной работы в школе на уроках физики, химии.
Добиться успеха в формировании вычислительных навыков можно только в том случае, если четко соблюдать некоторые требования к проведению устных упражнений:
четкое объяснение учителем цели задания;
наличие наглядности, художественного слова, дополнительного материала;
учет времени;
подведение итога устных упражнений микрообобщением или оценивание детей за хорошие успехи.
 12=276
12=276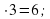 б)2
б)2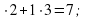 в)1
в)1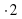 =2
=2 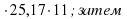 на применение законов сложения и вычитания:
на применение законов сложения и вычитания: 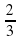
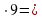 (6+
(6+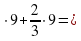 54+6=60.
54+6=60.