Департамент образования
и социально-правовой защиты детства
Администрации города Нижнего Новгорода
Муниципальное образовательное учреждение Лицей № 36
просп. Кирова, д. 29А, г. Нижний Новгород, 603101, тел./факс (831) 293-62-78,
e-mail: [email protected]
Научное общество учащихся
Время, вперед!
Выполнил:
ученик 6 класса А
Жуков Максим Дмитриевич
Проверил: учитель первой квалификационной категории
Ермейкина М.Ю.
Нижний Новгород
2014
Оглавление
Введение...............................................................................................................3
1. История возникновения часов. Этапы развития часовых механизмов.........5
2. Задачи с песочными часами...........................................................................13
3. Задачи с часами с циферблатом.....................................................................15
4. Задачи с электронными часами.....................................................................17
5. Парадоксы времени.........................................................................................18
Заключение.........................................................................................................23
Использованная литература..............................................................................25
Приложение........................................................................................................26
Введение
Задачи, несомненно, способствуют развитию смекалки и сообразительности. Каждодневное стремление развитого человека к познанию объясняет тот факт, что занимательная математическая задача доставляет не меньшее удовольствие, чем остроумный анекдот. Каждый день появляется много прекрасных математических задач с новыми идеями, требующими для решения нестандартного подхода и сообразительности. Это связано и с развитием самой математики, и с увеличивающимся интересом к задачам математических олимпиад разного уровня — от школьных до международных.
Текстовым задачам в курсе математики начальной и основной школы уделено достаточно много времени. Основными видами таких задач являются задачи на движение, на работу, на проценты, на переливание. Учащиеся уже с начальной школы знакомятся с методами решения задач такого вида. Помимо этих задач можно выделить еще группы задач, которым в школьном курсе практически не уделяется времени.
На занятиях математического кружка учитель попросил найти задачи, в содержании которых упоминается термин "часы". Оказывается, что задач про "часы" очень много. Они всегда интересны и познавательны.
Данная работа посвящена одному типу текстовых задач - задач, в содержании которых встречается термин "часы". Были проанализированы задачи из школьных учебников по математике 5-6 классов, олимпиады различного уровня за предыдущие года; ознакомился со статьями из различных журналов. Несмотря на обилие задач с таким содержанием, виды и методы их решения не систематизированы.
Цель работы: систематизировать виды задач, в содержании которых встречается термин "часы".
Цель работы определила следующие частные задачи:
ознакомиться с историей возникновении часов и этапами их развития;
выделить виды задач, в содержании которых встречается термин "часы";
проиллюстрировать выделенные виды конкретными задачами;
рассмотреть некоторые парадоксы времени.
Работа состоит из введения, пяти параграфов, заключения, списка литературы и приложения.
Первый параграф посвящен истории возникновения часовых механизмов.
Во втором параграфе предпринята попытка выделить виды задач, в тексте которых идет речь о песочных часах. Рассмотрены примеры решения задач с использованием песочных часов.
В третьем параграфе рассмотрены виды задач, в тексте которых речь идет о часах с циферблатом. Приведены примеры решения задач с использованием механических часов.
В четвертом параграфе произведена попытка выделить блок задач, в тексте которых речь идет об электронных часах. Представлены решения задач с электронными часами.
В пятом параграфе рассмотрены некоторые парадоксы времени.
В Приложении размещена "книжка - малышка", в которой собраны задачи, содержащихся в работе, с решениями по каждому виду.
Список литературы состоит из 10 источников.
1. История возникновения часов. Этапы развития часовых механизмов
Д ля того, чтобы лучше узнать ответ на вопрос, что такое время, давайте заглянем в историю и узнаем, как и чем измеряли время раньше.
ля того, чтобы лучше узнать ответ на вопрос, что такое время, давайте заглянем в историю и узнаем, как и чем измеряли время раньше.
Путь, пройденный человечеством с глубокой древности до наших дней, можно представить различным образом - можно описать его как вереницу великих событий, как серию биографий великих людей, можно отразить этот путь через историю философии, литературы или искусства, через историю войн и еще многими другими способами. В настоящем реферате мы попытаемся показать развитие человеческой мысли через историю великого изобретения - часов. Пытливый человеческий разум изобрел для измерения времени целый ряд инструментов, например, солнечные, водяные, свечные часы, которые использовались вплоть до XVIII века, затем песочные часы и от XVI до XVIII века масляные часы. Однако из-за своей зависимости от внешних условий и их колебаний, равно как и из-за технического несовершенства эти средства измерения времени не нашли всеобщего применения.
По крайней мере, 4000 лет назад уже повсюду существовали часы различной степени сложности. Первыми попытались их сделать египтяне, которые изобрели звездные часовые карты, и можно было определить ночное время, наблюдая за подъемом звезд.
1.1. Солнечные часы
Археологические исследования показывают, что солнечные часы существовали и до древнего Вавилона. Самые старые из найденных часов датируются пятью тысячелетиями до нашей эры. Из Вавилона к нам пришло деление суток на двадцать четыре часа, а часа на 60 минут.
Особо благоприятные климатические условия для измерения времени с помощью солнечных часов имел Египет. Известия о самых древних из древнеегипетских солнечных часов относится к эпохе правления Тутмоса III - первой половине XV в. до н.э. Одним из видов солнечных часов были ступенчатые часы в виде обелиска с двумя наклонными поверхностями, ориентированными по оси на восток - запад и разделенными на ступени. При восходе Солнца тень падала на край верхней ступеньки одной из этих поверхностей - восточной, затем постепенно опускалась, пока к полудню полностью не исчезала. Затем, после полудня, тень снова появлялась в нижней части западной поверхности, откуда она все поднималась до тех пор, пока при заходе Солнца не касалась грани верхней ступеньки.
Н
 а описанных солнечных часах время измерялось длиной, а не направлением отбрасываемой тени. Однако египтяне имели солнечные часы и со шкалой для определения направления отбрасываемой тени.
а описанных солнечных часах время измерялось длиной, а не направлением отбрасываемой тени. Однако египтяне имели солнечные часы и со шкалой для определения направления отбрасываемой тени.

1.2. Водяные часы
Солнечные часы были простым и надежным указателем времени, но страдали некоторыми серьезными недостатками: их работа зависела от погоды и была ограничена временем между восходом и заходом Солнца. Нет сомнений, что из-за этого ученые стали изыскивать иные пути измерения времени, не связанные с наблюдением небесных тел. Также понятно, что новые приборы измерений времени должны были принципиально отличаться от солнечных часов.
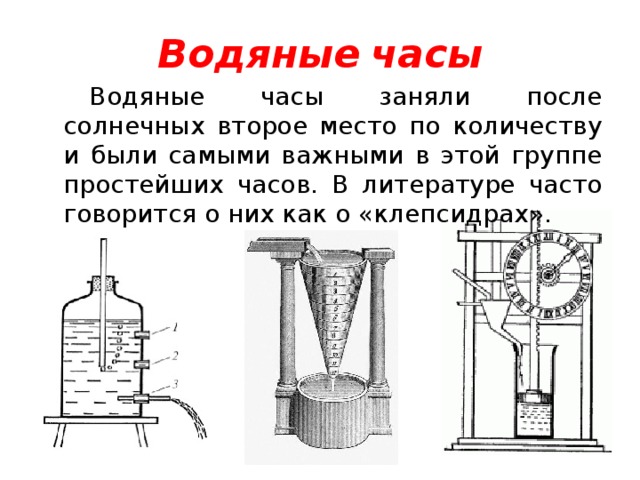
Водяные часы заняли после солнечных второе место по количеству и были самыми важными в этой группе простейших часов. В литературе часто говорится о них как о «клепсидрах». Это наименование происходит от сочетания двух греческих слов klepto – брать и idor – вода. Многие, судя по греческому наименованию, ошибочно считают, что именно в Греции они были придуманы. Однако дело обстоит не так: в примитивном виде водяные часы были известны уже египтянам, у которых сохранились, по всей вероятности, самые старые водяные часы в мире.
Прибор каждый вечер заполнялся водой, чтобы определить ночное время. Вода постепенно вытекала через тростниковую втулку на дне. Ход времени определялся опусканием воды за отметки "часа". Так ночь делили на 12 частей независимо от времени года, "время" на часах варьировалось по длине в течение года. Таким образом, 12 линий "часовых" отметок слегка р азличаются по высоте.
азличаются по высоте.


1.3. Огневые часы
П
 омимо солнечных и водяных, с начала XIII века появились и первые огневые, или свечные, часы. Это тонкие свечи длиной около метра с нанесенной по всей длине шкалой. Они сравнительно точно показывали время, а в ночные часы еще и освещали жилища.К боковым сторонам свечи иногда прикрепляли металлические штырьки, которые по мере выгорания и таяния воска падали, и их удар по металлической чашке подсвечника был своего рода звуковой сигнализацией времени.
омимо солнечных и водяных, с начала XIII века появились и первые огневые, или свечные, часы. Это тонкие свечи длиной около метра с нанесенной по всей длине шкалой. Они сравнительно точно показывали время, а в ночные часы еще и освещали жилища.К боковым сторонам свечи иногда прикрепляли металлические штырьки, которые по мере выгорания и таяния воска падали, и их удар по металлической чашке подсвечника был своего рода звуковой сигнализацией времени.
Определить время появления таких часов сложно, однако можно сказать наверняка, что произошло это не раньше, чем научились производить в достаточном количестве стекло.
Больше всего лампадных часов было в Китае, который вообще считается колыбелью всех видов огневых часов.До сих пор в Китае рассказывают, что примерно 3000 лет назад Фо-хи, «отец Китая» и его первый император, создал первые огневые часы, чтобы с их помощью измерять дневное и ночное время.
Н аиболее типичные для Китая фитильные часы имели форму дракона, в хребте которого укреплялся специальный держатель для палочки. Скорость сгорания фитиля зависела от многих обстоятельств, и для определения ее требовался большой опыт. Такие часы никогда не относились к приборам, которые по точности можно было бы сравнить с солнечными или водяными часами. Причем наличие всех этих часов в Китае не дает никакой хронологической отметки и, во всяком случае, не означает их древности.
аиболее типичные для Китая фитильные часы имели форму дракона, в хребте которого укреплялся специальный держатель для палочки. Скорость сгорания фитиля зависела от многих обстоятельств, и для определения ее требовался большой опыт. Такие часы никогда не относились к приборам, которые по точности можно было бы сравнить с солнечными или водяными часами. Причем наличие всех этих часов в Китае не дает никакой хронологической отметки и, во всяком случае, не означает их древности.
1.4. Песочные часы
Д
 ата возникновения песочных часов неизвестна. Однако по сохранившимся данным можно полагать, что принцип песочных часов был известен в Азии значительно раньше начала нашего летоисчисления. Обычно песочные часы рассчитывались на работу в течение получаса или часа. Реже встречались песочные часы, рассчитанные на непрерывное измерение времени в течение 3 часов, и лишь в совершенно редких случаях строили огромные песочные часы, рассчитанные на 12 часов хода.
ата возникновения песочных часов неизвестна. Однако по сохранившимся данным можно полагать, что принцип песочных часов был известен в Азии значительно раньше начала нашего летоисчисления. Обычно песочные часы рассчитывались на работу в течение получаса или часа. Реже встречались песочные часы, рассчитанные на непрерывное измерение времени в течение 3 часов, и лишь в совершенно редких случаях строили огромные песочные часы, рассчитанные на 12 часов хода.
Производство стеклянных колб для песочных часов было возможно благодаря известной уже производственной технологии прозрачного стекла и его формирования в полые сферические колбы. В суженное горлышко в месте стыка обеих колб после заполнения песком вкладывалась небольшая горизонтальная металлическая диафрагма с отверстием, регулирующая количество и скорость пересыпания зернышек песка. Место стыка перевязывалось плотной ниткой и закреплялось смолой. Точность песочных часов зависела также от формы колб, от гладкости их внутренних стенок, от равномерности прохождения песка через регулирующую диафрагму в горлышке, но прежде всего - от равномерной зернистости и сыпучести данного песка.
П

 есочные часы никогда не достигали точности солнечных часов. Кроме того, при длительном пользовании такими часами, их точность изменялась, поскольку зерна песка постепенно дробились на более тонкие, а отверстие в середине диафрагмы постепенно истиралось и увеличивалось, так что скорость прохождения песка через них становилась большей.
есочные часы никогда не достигали точности солнечных часов. Кроме того, при длительном пользовании такими часами, их точность изменялась, поскольку зерна песка постепенно дробились на более тонкие, а отверстие в середине диафрагмы постепенно истиралось и увеличивалось, так что скорость прохождения песка через них становилась большей.
1.5. Механические часы
Солнечные, водяные и огневые хронометрические приборы завершили первую фазу в развития приборов для измерения времени. Постепенно выработались более четкие представления о времени, и стали изыскиваться более совершенные способы его измерения. Революционным изобретением, ознаменовавшим совершенно новые этапы развития в этом направлении, было создание первых колесных часов, с появления которых началась современная эра хронометрии.
Механические часы были нужны всем, церкви – для уточнения начала времени богослужения, в светских делах требовалось знать точное время для свершения коммерческих сделок. Точное время хотели знать и на производствах, где результат работы зависел от времени продолжительности технологических процессов.
Во всех таких случаях было нельзя обойтись без механических часов. Международная торговля, тоже, без механических часов обойтись не могла, значительное расширение морских торговых путей требовало точных методов навигации.
Для производства механических часов, какими были первые образцы, требовались гораздо более точные станки, чем весь прежний инструментарий. Современное точное машиностроение родилось из мастерства механиков часовщиков.
Известны старинные французские и английские башенные часы простого устройства с боем, но без циферблата. Английское слово clock – часы, происходит от латинского clocca; другим его эквивалентом является саксонское clugge французское cloche и древнегерманское (тевтонское) glocke, но первоначально все эти слова обозначали не часы, а колокол.
Б
 ашенные часы были довольно капризным механизмом, требующим постоянного наблюдения. В течение дня несколько раз приходилось поднимать груз. Ход часов зависел от силы трения, поэтому они нуждались в постоянной смазке. Погрешность их суточного хода по современным меркам была очень велика. Но, несмотря на это, они долгое время оставались самым точным и распространенным прибором для измерения времени. С каждым десятилетием механизм часов усложнялся. С часами стали связывать множество других приспособлений, выполнявших самые различные функции. В конце концов, башенные часы превратились в сложное устройство со многими стрелками, автоматическими подвижными фигурами, разнообразной системой боя и великолепными украшениями.
ашенные часы были довольно капризным механизмом, требующим постоянного наблюдения. В течение дня несколько раз приходилось поднимать груз. Ход часов зависел от силы трения, поэтому они нуждались в постоянной смазке. Погрешность их суточного хода по современным меркам была очень велика. Но, несмотря на это, они долгое время оставались самым точным и распространенным прибором для измерения времени. С каждым десятилетием механизм часов усложнялся. С часами стали связывать множество других приспособлений, выполнявших самые различные функции. В конце концов, башенные часы превратились в сложное устройство со многими стрелками, автоматическими подвижными фигурами, разнообразной системой боя и великолепными украшениями.
Так, в Пражских башенных часах (сооруженных в 1402 году) перед боем раскрывались два оконца над циферблатом и из них выходило 12 апостолов. Страшная фигура Смерти, стоявшая на правой стороне циферблата, держала в руках косу и песочные часы. При каждом бое часов она поворачивала косу, а затем песочные часы, напоминая о конце жизни. Человек, стоявший рядом, кивал головой, как бы подчеркивая роковую неизбежность. На другой стороне циферблата находились еще две фигуры. Одна изображала человека с кошельком в руках; каждый час он звенел лежавшими там монетами, показывая, что время - деньги. Другая фигура - путника, мерно ударявшего посохом в землю. Она показывала, как с течением времени движется по жизненной дороге человек, или суетность жизни. После боя часов появлялся петух и три раза кричал. Последним в оконце появлялся Христос и благословлял всех стоявших внизу зрителей. Создание таких автоматов требовало особых программных устройств. Их приводил в движение большой диск, управляемый часовым механизмом. Все подвижные части фигур имели свои рычаги. Во время вращения круга они то поднимались, то опускались, когда рычаги попадали в особые вырезы и зубцы вращающегося диска. Помимо этого башенные часы имели отдельный механизм для боя (многие часы по-разному отбивали четверть часа, час, полдень и полночь), приводимый в движение собственной гирей, и четыре циферблата (на каждой стороне башни).





1.6. Атомные часы
До 40-х годов XX в. приборы времени были основаны только на использовании колебаний механических осцилляторов – маятника, баланса со спиральной пружиной и кристалла кварца. У этих и других осцилляторов, имеющих макроразмеры, собственная частота колебаний в значительной степени зависит от ряда дестабилизирующих факторов (температуры, барометрического давления, степени старения материалов и т.д.). Поэтому они не могут обладать такой высокой стабильностью, какая нужна для точного измерения времени.
В последние десятилетия развитие атомной физики и микроволновой радиоспектроскопии привело к созданию принципиально нового эталона частоты и времени на атомных постоянных, разработанного на основе изобретения молекулярных и атомных часов. Последние основаны на применении таких осцилляторов, как атом и молекула, частота колебаний которых в микромире строго стабильна и не зависит от внешних воздействий и для которых справедливы законы квантовой механики. В молекулярных часах в качестве осцилляторов используются группы молекул, в атомных часах – группы отдельных атомов.
П
 оявление и развитие этих приборов времени произвело революцию в области измерения времени. Она явилась одним из важных направлений научно-технической революции XX в.
оявление и развитие этих приборов времени произвело революцию в области измерения времени. Она явилась одним из важных направлений научно-технической революции XX в.
2. Задачи с песочными часами
В этом параграфе рассмотрены задачи, в содержании которых речь идет о песочных часах. Как с помощью двух часов разной длительности отмерить определенный промежуток времени.
этом параграфе рассмотрены задачи, в содержании которых речь идет о песочных часах. Как с помощью двух часов разной длительности отмерить определенный промежуток времени.
2. Нам нужно испечь яблочный пирог. Обычных часов у нас нет, но есть двое песочных часов. Одни рассчитаны на 7 минут, а другие на 11 минут. Как нам точно отмерить 15 минут, необходимых для приготовления пирога.
Решение
Переворачиваем часы на 11 и 7 минут одновременно;
Когда закончатся 7 минут включаем пирог;
Ждем еще 4 минуты и по завершению 11 минут, переворачиваем часы на 11 минут еще раз;
Выжидаем 11 минут – пирог готов.
3. При помощи только 4- и 7-минутных песочных часов точно отмерьте девять минут
Решение
1) Запустите 4- и 7-минутные часы одновременно
2) Когда в 4-минутных часах закончится песок, переверните их (итоговое время - 4 минуты)
3) Когда в 7-минутных часах закончится песок, их тоже переворачиваем. В этот момент в 4-минутных часах, в верхней половинке, осталось песка на 1 минуту (итоговое время - 7 минут)
4) Когда 4-минутные часы опустеют, переворачиваем 7-минутные, где в нижней половине песка на 1 минуту (итоговое время 8 минут)
5) Когда 7-минутные опустеют, прошло ровно 9 минут
4. "Кораблекрушение" . Вы - капитан корабля. Вы потерпели кораблекрушение и попали в плен к каннибалам. Вам в руки дают пару песочных часов. В одних песка хватит ровно 4 минуты, в других ровно 7. Вождь требует, чтобы вы сказали, когда пройдет точно 9 минут с момента, как он даст команду. Для контроля за вами у вождя есть 9-ти минутные часы. Вот по ним он и будет следить за вашими действиями.
Если вы выполните задание верно, то вас освободят. Если вы не сделаете этого, то вас съедят.
Начинать отсчет времени нужно немедленно, без всякой подготовки.
Можно часы запускать одновременно, а можно в разное время.
Можно остановить отсчет в любых часах в любой момент времени, а в других продолжать.
Если в любых часах закончил падать песок, не обязательно их сразу же переворачивать
Решение
1) Одновременно запустить всё, когда закончатся 4 перевернуть их, когда закончатся 7 перевернуть их, когда второй раз закончится 4 снова перевернуть 7 (там будет одна минута) - получается 9 мин.
2) Одновременно запустить и те, и те часы. Каждые запускать 3 раза без промежутков. Начать отсчёт, когда 3 раз закончатся часы на 4 минуты, закончить, когда трижды закончатся часы на 7 минут.
При решении задач такого типа необходимо выполнять все возможные пересыпания, не приводящие к ранее встречавшимся распределениям песка по часам.
3. Задачи с часами с циферблатом
В этот параграф собраны задачи, в содержании которых речь идет о механических часах.
1. Сколько раз в течение суток минутная и часовая стрелки составляют прямой угол?
Решение
В течение суток минутная стрелка совершает 24 оборота, а часовая - 2 оборота, следовательно минутная стрелка совершает 22 оборота вокруг часовой, составляя при этом с часовой стрелкой дважды прямой угол (отставая на четверть круга и обгоняя на четверть круга). Таким образом, прямой угол между стрелками образуется за сутки 44 раза.
2. Определите чему равен угол между часовой и минутной стрелками часов в 23 часа 45 минут?
Решение
Угол между минутной стрелкой и отметкой "12" на циферблате равен 900, а угол между часовой стрелкой и отметкой "12"равен 1/4 от угла между "11" и "12", т.е. равен 300 : 4 = 70 30/. Тогда искомый угол равен 900 - 7030/ = 82030/
3. Какой угол составляют стрелки часов в 9 ч 20 мин?
Решение
В 9 ч угол между стрелками равен 900. За час часовая стрелка проходит 1/12 часть окружности, т.е. 300 а за 20 мин пройдет 1/3 этого угла, т.е. 100. Аналогично минутная стрелка, проходящая за час 3600, за 20 мин пройдет 1200. Таким образом, угол в 900 уменьшится на 100 и увеличится на 120', став равным 2000, дополнительный к нему угол будет равен 1600.
4. Сколько раз в сутки стрелки часов совпадают?
Решение
Пусть на часах 12 часов. Следующее совпадение стрелок наступит тогда, когда минутная стрелка опередит часовую на один оборот. Каждый час минутная стрелка опережает часовую на 1-1/12 = 11/12 оборота. Следовательно, через каждые 1:11/12 = 12/11 стрелки будут совпадать. Число этих совпадений в сутки равно 24 : 12/11 = 22. Различных случаев совпадения 11.
5 . Придворный астролог царя Гороха называет время суток хорошим, если на часах с тремя стрелками на одной оси мы видим после часовой стрелки (по ходу часов) сначала минутную, а потом секундную. Какого времени в сутках больше: хорошего или плохого? (Стрелки движутся с постоянной скоростью)
. Придворный астролог царя Гороха называет время суток хорошим, если на часах с тремя стрелками на одной оси мы видим после часовой стрелки (по ходу часов) сначала минутную, а потом секундную. Какого времени в сутках больше: хорошего или плохого? (Стрелки движутся с постоянной скоростью)
6. В некоторый момент времени двое стрелочных часов показывают верное время. Через какое время наступит такой следующий момент, если известно, что одни часы отстают на 5 минут каждый час, а другие спешат на 4 минуты каждый час?
Решение
Первые часы отстают на 1 оборот каждые 144 часа, вторые уходят вперед на 1 оборот каждые 180 часов. НОК (144, 180) = 720
7. На часах Клауса минутные деления нанесены небольшими штрихами. Взглянув на часы в шестом часу по полудни, Клаус обнаружил, что большая стрелка отстоит от малой на три деления. Сколько было на часах?
Решение
В 5.00 минутную стрелку отделяют от часовой 25 минутных делений. в тот момент, когда Клаус взглянул на часы, большая стрелка отстояла от малой лишь на 3 деления и, следовательно, успела пройти 22 деления. За 1 минуту большая стрелка проходит одно деление, а малая - 1/12 деления. Следовательно, за 1 минуту минутная стрелка догоняет часовую на 1-1/12 = 11/12 деления, а для того, чтобы пройти 22 деления, минутной стрелке понадобиться 22:11/12 = 24 минуты. Значит, Клаус взглянул на часы в 5 часов 24 минуты.
Следует отметить, что это далеко не полный перечень возможных задач, в которых речь идет о механических задач.
4. Задачи с электронными часами
В этом параграфе выделены задачи, в содержании которых речь идет об электронных часах.
1. На электронных часах высвечивается время: часы и минуты. Сколько времени в сутки на их табло присутствует хотя бы в одном месте цифра 2? Найдите соответствующее время для остальных цифр: 0,1,3,4.....9.
Решение
На первом месте цифра 2 бывает в течение 4 ч от 20.00 до 00.00. В остальные 20 ч она бывает 2 ч на втором месте — от 02.00 до 03.00 и от 12.00 до 13.00. В оставшиеся 18 ч цифра 2 бывает на третьем месте по 10 мин каждый из часов, в остальные 50 мин часа еще по 5 мин на четвертом месте. Итого, по 15 мин в каждый из 18 ч, т.е. 4 ч 30 мин. Всего получаем 4 + 2 + 4,5 = 10,5 ч. Для цифр 0 и 1 аналогично получаем 16 ч, для цифры 3 — 8,25 ч, для цифр 4 и 5 — по 7,5 ч, для остальных — по 4,2 ч.
2. Сколько времени в течение суток на табло электронных вокзальных часов светится хотя бы одна цифра 2 (часы не показывают секунды)?
Решение
В течение суток есть 6 часов, в обозначении которых есть цифра 2 (2 часа ночи, 12 часов, 20, 21, 22, 23). В каждом из оставшихся часов это время равно 15 минутам (с 20 по 29 минуту и по одной в остальных десятиминутках). Всего 6 + 18 × 1/4 = 10,5 ч.
3. Представьте, что у Вас есть электронные цифровые часы, которые показывают время в 12 часовом режиме (т.е. не в 24 часовом). Эти часы сломались и показывают время только в том случае, если количество часов и минут совпадает, например, 1:01, 2:02, 3:03 и т.д. Какой самый минимальный промежуток времени между показаниями данных часов?
Решение
Самые близкие показания между 12:12 и 1:01. Ответ: 49 минут.
Основным способом решения задач такого вида можно было бы считать метод перебора возможных вариантов.
Парадоксы времени
Теория перемещения во времени
Научная фантастика в ряде случаев предсказывала такие изобретения, которые казались совершенно нереализуемыми с точки зрения того времени, когда произведение издавалось. Однако шло время и со страниц фантастических романов в реальную жизнь перешли подводные лодки, самолеты и космические корабли, роботы и компьютеры.
Прошло достаточно много лет с того момента, когда Герберт Уэлс представил читателю свою гениальную «Машину времени». За это время ученый мир коренным образом изменил свое отношение к этой идее. Многие известные физики сегодня заявляют, что теоретических препятствий для столь удивительного путешествия не существует. Однако до недавнего времени стройного математического описания такого процесса не существовало. Эту задачу взялся решить Амос Ори, профессор Израильского технологического института, и ему это удалось! Израильтянин сумел поставить фактически фантастическую гипотезу на «научные рельсы». Теория перемещения во времени профессора Ори отныне позволяет уверенно говорить о том, что теоретически машина времени может быть создана. По мысли автора, в случае придания простанственно-временному континууму форму воронки или кольца, появится возможность перемещения в прошлое. Каждый новый виток подобной структуры будет уводить путешественника все глубже в толщу веков.
Время – величина, ускользающая от понимания человека. Только в XX веке начали возникать теории, пытавшиеся описать сущность времени. Поэтому, работы по исследованию этой физической величины всегда окутаны покровом таинственности.
Сегодня мало кто знает, что по степени научного предвидения ГербертУэллс вышел на первое место, обогнав в этом вопросе даже Жюля Верна. Этот вопрос выяснился только через сто лет. Для объяснения такой непостижимой прорицательности режиссеры Голливуда предложили следующее объяснение: книга Герберта Уэллса "Машина времени" – это ни что иное, как автобиографичный роман. Уэллсу удалось изобрести устройство для перемещения во времени, побывать в будущем и узнать в нем столько потрясающих фактов, что этого хватило на всю последующую жизнь писателя. В результате этой идеи появился одноименный фильм "Машина времени". У этого “безумного” объяснения есть серьезные аргументы: из всех предсказанных автором событий, сбылось более 80 процентов его предсказаний, а еще пять неосуществившихся новшеств могут быть реализованы в ближайшие годы! Для совпадения это слишком большой процент! Но самой таинственной, самой ускользающей от понимания, все же остается первая идея Герберта Уэллса – машина времени. Можно ли вообще о ней рассуждать? В настоящее время о времени уже известно несколько больше, чем столетие назад, и мы можем говорить об этом вопросе более определенно. что до достижения ими Парадоксы времени
Кроме потенциальных проблем технического плана, ученые рассматривают возможные конфликты времени. В частности, так называемые парадоксы времени вполне могут стать реальной проблемой. Их будет немало, и все они будут иметь отношение к воздействию на ход случившихся событий.
О сновная масса физиков-теоретиков при обсуждении хронопутешествий достигли согласия в вопросе о том, что любое воздействие на ход совершившихся событий формирует параллельную реальность либо отдельную «мировую линию», не противоречащую существованию исходной. Причем общее количество этих новых реальностей будет составлять столько, сколько необходимо для непротиворечивого существования каждой из них.
сновная масса физиков-теоретиков при обсуждении хронопутешествий достигли согласия в вопросе о том, что любое воздействие на ход совершившихся событий формирует параллельную реальность либо отдельную «мировую линию», не противоречащую существованию исходной. Причем общее количество этих новых реальностей будет составлять столько, сколько необходимо для непротиворечивого существования каждой из них.
Знаменитый английский астрофизик Стивен Хокинг сказал астрофизику НАСА Карлу Сагану, что если бы возможность перемещения во времени существовала, то среди людей находилось бы много ребят из будущего, на что тот заметил о наличии множества способов опровергнуть данное заявление. Он посоветовал почитать Льюиса Кэрролла и уподобил нору, в которую падает Алиса, «червоточине» Торна. Может быть, машина времени способна переносить лишь в будущее или недалекое прошлое, а наше время «расположено» слишком давно. Или, возможно, обитатели будущего способны перемещаться только к тем, у кого тоже есть машина времени.
Критиков у идеи перемещения во времени хватает, но опровергнуть саму концепцию никто так и не смог, поэтому гипотетическая возможность в любом случае сохраняется. Кроме того, пока спорщики обсуждают теории, практические разработки идут полным ходом. Так, в июле 2010 г. в прессе появилось сообщение, что физики описали закон природы, который позволяет преодолеть парадокс дедушки. Причем это вполне практические эксперименты, правда, лишь на квантовых частицах, но главное здесь — сам принцип. Суть гипотезы в следующем: странник во времени не сможет умертвить собственного дедушку, поскольку у природы есть некий защитный механизм, в результате чего что-нибудь изменит траекторию пули, ножа или кирпича или что-то случится при подготовке убийства и т. д.
Занимательную идею высказал и специалист по квантовым вычислениям Сет Ллойд из Массачусетского технологического института вместе с другими учеными из США, Италии и Японии. Они предположили, что машину времени можно сконструировать с учетом квантовой механики замкнутых временных кривых, представляющих собой мировые линии, влекущие материальную частицу в исходную точку.
Ученые утверждают, что квантовые путешествия во времени не требуют классического пути из будущего в прошлое. К тому же их теория базируется на «последующем выборе», поэтому обеспечивает самопроизвольное разрешение парадоксов времени — в ходе такого путешествия может случиться только то, что может произойти в обычной квантовой механике, т. е. все происходящее после включения машины времени вполне может случиться и без нее. Соответственно, когда машина будет включена, то не произойдет ничего, что может повлечь за собой парадокс времени. Теорию о том, что Вселенная защищается от парадоксов, ученые проверили на фотонах. Конечно, в прошлое их не отправляли, но, комбинируя соответствующим образом квантовые состояния, создавали для частиц ситуацию, близкую к парадоксу дедушки. В результате выяснилось, что, чем ближе к парадоксальному состоянию находились фотоны, тем реже опыт завершался успехом. Физики естественно предположили, что у путешествий во времени имеется такой же природный «предохранитель».
Парадокс Ахиллеса и черепахи.
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Парадокс дедушки
Предлагаемый парадокс, касающийся путешествия во времени, впервые описанный (именно под этим названием) писателем-фантастом Рене Баржавелем в своей книге 1943 года Le Voyageur Imprudent.
Парадокс заключается в следующем: предположим, что человек с помощью машины времени отправился назад в прошлое и убил своего биологического деда до того, как последний встретил бабушку путешественника. В результате один из родителей путешественника (и, как следствие, сам путешественник) никогда бы не был рождён. Это означает, что он в конечном итоге не мог бы путешествовать во времени, что, в свою очередь, означает, что его дед остался бы жив и путешественник был бы рождён, а это позволило ему путешествовать во времени и убить своего дедушку. Таким образом, каждая возможность подразумевает отрицание самой себя, создавая логический парадокс. Вариант его разрешения следующий: тот факт, что путешественник во времени живёт в настоящее время, означает, что он просто не стремится убить своего прародителя. Это означает, что можно действовать с полной свободой, но, что бы вы ни делали в прошлом, не можете изменить настоящее, потому что его последствия уже ощущаются.
Несмотря на название, парадокс убитого дедушки рассматривает не только невозможность собственного рождения. В первую очередь он касается любых действий, которые делают невозможным возможность путешествия во времени. Пример названия парадокса является лишь наиболее часто «приходящим в голову», если выбирать из всего спектра подобных возможных действий. Другим примером может быть использование научных знаний для изобретения машины времени, последующее возвращение назад во времени и (будь то убийство или иное) препятствование работе учёных над тем, что в конечном итоге приведёт к получению информации, которую вы использовали, чтобы изобрести машину времени. Эквивалентный парадокс известен в философии как «автоинфантицид»: возвращение в прошлое и убийство самого себя в детстве.
Парадокс убитого дедушки часто используется для утверждения о том, что путешествие во времени в прошлое невозможно. Тем не менее, был предложен ряд гипотез, чтобы избежать парадокса: такие, как предположение о том, что прошлого изменить нельзя, поэтому дед уже должен был пережить покушение на убийство (как говорилось ранее), или же что путешественник во времени создаёт альтернативную линию времени, в которой он никогда не будет рождён.
Заключение
Задачи, несомненно, способствуют развитию смекалки и сообразительности. Каждодневное стремление развитого человека к познанию объясняет тот факт, что занимательная математическая задача доставляет не меньшее удовольствие, чем остроумный анекдот. Каждый день появляется много прекрасных математических задач с новыми идеями, требующими для решения нестандартного подхода сообразительности.
Это связано и с развитием самой математики, и с увеличивающимся интересом к задачам математических олимпиад разного уровня — от школьных до международных.
В работе была прослежена история развития часов вплоть до наших дней: солнечные, водяные, свечные часы, которые использовались вплоть до XVIII века, затем песочные часы и от XVI до XVIII века масляные часы. Однако из-за своей зависимости от внешних условий и их колебаний, равно как и из-за технического несовершенства эти средства измерения времени не нашли всеобщего применения. Солнечные, водяные и огневые хронометрические приборы завершили первую фазу в развития приборов для измерения времени. Постепенно выработались более четкие представления о времени, и стали изыскиваться более совершенные способы его измерения. Революционным изобретением, ознаменовавшим совершенно новые этапы развития в этом направлении, было создание первых колесных часов, с появления которых началась современная эра хронометрии. До 40-х годов XX в. приборы времени были основаны только на использовании колебаний механических осцилляторов – маятника, баланса со спиральной пружиной и кристалла кварца. В последние десятилетия развитие атомной физики и микроволновой радиоспектроскопии привело к созданию принципиально нового эталона частоты и времени на атомных постоянных, разработанного на основе изобретения молекулярных и атомных часов. Появление и развитие этих приборов времени произвело революцию в области измерения времени. Она явилась одним из важных направлений научно-технической революции XX в.
В работе предпринята попытка выделить и систематизировать виды задач, в тексте которых идет речь о песочных часах. Как правило, формулировка задач одна и та же: с помощью нескольких песочных часов отмерить некоторый промежуток времени. При решении задач такого типа необходимо выполнять все возможные пересыпания, не приводящие к ранее встречавшимся распределениям песка по часам.
Кроме того, приведены примеры решения задач с использованием часов с циферблатом. По своему содержанию они самые разнообразные: найти угол между стрелками; определить сколько раз стрелки часов совпадут, определить точное время на часах если...
Так же предпринята попытка выделить и систематизировать задачи, в тексте которых речь идет об электронных часах. Основным способом решения таких задач мы считаем метод перебора возможных вариантов.
В заключении работы предложены некоторые парадоксы времени: парадокс Ахиллеса и черепахи, парадокс дедушки.
Во время выполнения работы мы ознакомились с большим количеством литературы. Также было решено множество задач, что помогло ознакомиться с их разнообразием не только по типу, но и по сложности.
Итак, частные задачи, которые были поставлены в начале работы, выполнены. Значит, цель работы достигнута.
Использованная литература
http://www.5egena5.ru/
http://www.objectiv-x.ru/peremeschenie-vo-vremeni/tonneli-vremeni.html
Альхова З.Н., Макеева А.В. Внеклассная работа по математике. - Саратов: Лицей, 2003
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. - М.: Мнемозина, 2006
Джеймс П., Торп Н. Древние изобретения. - ООО "Попурри", 1997
Задачи международного конкурса "Кенгуру", 2008, 2012, 2013
Зубарева И.И., Мордкович А.Г. Математика 6. - М.: Мнемозина, 2005
Михаль С. Часы. - М.: Знание, 1983
Фарков А.В. Математические кружки в школе. 5-8 класс. - М.: Айрис - пресс, 2006
Фарков А.В. Математические олимпиады в школе. 5-11 класс. - М.: Айрис - пресс, 2004
26

 ля того, чтобы лучше узнать ответ на вопрос, что такое время, давайте заглянем в историю и узнаем, как и чем измеряли время раньше.
ля того, чтобы лучше узнать ответ на вопрос, что такое время, давайте заглянем в историю и узнаем, как и чем измеряли время раньше. 
 а описанных солнечных часах время измерялось длиной, а не направлением отбрасываемой тени. Однако египтяне имели солнечные часы и со шкалой для определения направления отбрасываемой тени.
а описанных солнечных часах время измерялось длиной, а не направлением отбрасываемой тени. Однако египтяне имели солнечные часы и со шкалой для определения направления отбрасываемой тени.
 азличаются по высоте.
азличаются по высоте.


 омимо солнечных и водяных, с начала XIII века появились и первые огневые, или свечные, часы. Это тонкие свечи длиной около метра с нанесенной по всей длине шкалой. Они сравнительно точно показывали время, а в ночные часы еще и освещали жилища.К боковым сторонам свечи иногда прикрепляли металлические штырьки, которые по мере выгорания и таяния воска падали, и их удар по металлической чашке подсвечника был своего рода звуковой сигнализацией времени.
омимо солнечных и водяных, с начала XIII века появились и первые огневые, или свечные, часы. Это тонкие свечи длиной около метра с нанесенной по всей длине шкалой. Они сравнительно точно показывали время, а в ночные часы еще и освещали жилища.К боковым сторонам свечи иногда прикрепляли металлические штырьки, которые по мере выгорания и таяния воска падали, и их удар по металлической чашке подсвечника был своего рода звуковой сигнализацией времени. аиболее типичные для Китая фитильные часы имели форму дракона, в хребте которого укреплялся специальный держатель для палочки. Скорость сгорания фитиля зависела от многих обстоятельств, и для определения ее требовался большой опыт. Такие часы никогда не относились к приборам, которые по точности можно было бы сравнить с солнечными или водяными часами. Причем наличие всех этих часов в Китае не дает никакой хронологической отметки и, во всяком случае, не означает их древности.
аиболее типичные для Китая фитильные часы имели форму дракона, в хребте которого укреплялся специальный держатель для палочки. Скорость сгорания фитиля зависела от многих обстоятельств, и для определения ее требовался большой опыт. Такие часы никогда не относились к приборам, которые по точности можно было бы сравнить с солнечными или водяными часами. Причем наличие всех этих часов в Китае не дает никакой хронологической отметки и, во всяком случае, не означает их древности.
 ата возникновения песочных часов неизвестна. Однако по сохранившимся данным можно полагать, что принцип песочных часов был известен в Азии значительно раньше начала нашего летоисчисления. Обычно песочные часы рассчитывались на работу в течение получаса или часа. Реже встречались песочные часы, рассчитанные на непрерывное измерение времени в течение 3 часов, и лишь в совершенно редких случаях строили огромные песочные часы, рассчитанные на 12 часов хода.
ата возникновения песочных часов неизвестна. Однако по сохранившимся данным можно полагать, что принцип песочных часов был известен в Азии значительно раньше начала нашего летоисчисления. Обычно песочные часы рассчитывались на работу в течение получаса или часа. Реже встречались песочные часы, рассчитанные на непрерывное измерение времени в течение 3 часов, и лишь в совершенно редких случаях строили огромные песочные часы, рассчитанные на 12 часов хода.

 есочные часы никогда не достигали точности солнечных часов. Кроме того, при длительном пользовании такими часами, их точность изменялась, поскольку зерна песка постепенно дробились на более тонкие, а отверстие в середине диафрагмы постепенно истиралось и увеличивалось, так что скорость прохождения песка через них становилась большей.
есочные часы никогда не достигали точности солнечных часов. Кроме того, при длительном пользовании такими часами, их точность изменялась, поскольку зерна песка постепенно дробились на более тонкие, а отверстие в середине диафрагмы постепенно истиралось и увеличивалось, так что скорость прохождения песка через них становилась большей.
 ашенные часы были довольно капризным механизмом, требующим постоянного наблюдения. В течение дня несколько раз приходилось поднимать груз. Ход часов зависел от силы трения, поэтому они нуждались в постоянной смазке. Погрешность их суточного хода по современным меркам была очень велика. Но, несмотря на это, они долгое время оставались самым точным и распространенным прибором для измерения времени. С каждым десятилетием механизм часов усложнялся. С часами стали связывать множество других приспособлений, выполнявших самые различные функции. В конце концов, башенные часы превратились в сложное устройство со многими стрелками, автоматическими подвижными фигурами, разнообразной системой боя и великолепными украшениями.
ашенные часы были довольно капризным механизмом, требующим постоянного наблюдения. В течение дня несколько раз приходилось поднимать груз. Ход часов зависел от силы трения, поэтому они нуждались в постоянной смазке. Погрешность их суточного хода по современным меркам была очень велика. Но, несмотря на это, они долгое время оставались самым точным и распространенным прибором для измерения времени. С каждым десятилетием механизм часов усложнялся. С часами стали связывать множество других приспособлений, выполнявших самые различные функции. В конце концов, башенные часы превратились в сложное устройство со многими стрелками, автоматическими подвижными фигурами, разнообразной системой боя и великолепными украшениями.





 оявление и развитие этих приборов времени произвело революцию в области измерения времени. Она явилась одним из важных направлений научно-технической революции XX в.
оявление и развитие этих приборов времени произвело революцию в области измерения времени. Она явилась одним из важных направлений научно-технической революции XX в. этом параграфе рассмотрены задачи, в содержании которых речь идет о песочных часах. Как с помощью двух часов разной длительности отмерить определенный промежуток времени.
этом параграфе рассмотрены задачи, в содержании которых речь идет о песочных часах. Как с помощью двух часов разной длительности отмерить определенный промежуток времени. . Придворный астролог царя Гороха называет время суток хорошим, если на часах с тремя стрелками на одной оси мы видим после часовой стрелки (по ходу часов) сначала минутную, а потом секундную. Какого времени в сутках больше: хорошего или плохого? (Стрелки движутся с постоянной скоростью)
. Придворный астролог царя Гороха называет время суток хорошим, если на часах с тремя стрелками на одной оси мы видим после часовой стрелки (по ходу часов) сначала минутную, а потом секундную. Какого времени в сутках больше: хорошего или плохого? (Стрелки движутся с постоянной скоростью) сновная масса физиков-теоретиков при обсуждении хронопутешествий достигли согласия в вопросе о том, что любое воздействие на ход совершившихся событий формирует параллельную реальность либо отдельную «мировую линию», не противоречащую существованию исходной. Причем общее количество этих новых реальностей будет составлять столько, сколько необходимо для непротиворечивого существования каждой из них.
сновная масса физиков-теоретиков при обсуждении хронопутешествий достигли согласия в вопросе о том, что любое воздействие на ход совершившихся событий формирует параллельную реальность либо отдельную «мировую линию», не противоречащую существованию исходной. Причем общее количество этих новых реальностей будет составлять столько, сколько необходимо для непротиворечивого существования каждой из них.

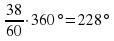 , а часовая на угол, в 12 раз меньший, т.е. 19. Следовательно, в 7 часов 38 минут угол между стрелками будет равен 210 + 19 - 228=1
, а часовая на угол, в 12 раз меньший, т.е. 19. Следовательно, в 7 часов 38 минут угол между стрелками будет равен 210 + 19 - 228=1

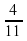 , минутная и часовая стрелки образуют прямой
, минутная и часовая стрелки образуют прямой 
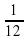

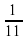
 оборота.
оборота.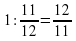 стрелки будут совпадать. Число этих совпадений в сутки равно 24:
стрелки будут совпадать. Число этих совпадений в сутки равно 24: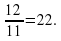 Различных случаев совпадения 11.
Различных случаев совпадения 11.

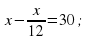
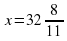 .
.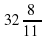 минут после того, как минутная и часовая стрелки совпадут, они будут «смотреть» в противоположные стороны.
минут после того, как минутная и часовая стрелки совпадут, они будут «смотреть» в противоположные стороны.


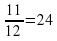 минуты. Итак, Клаус взглянул на часы в 5 часов 24 минуты.
минуты. Итак, Клаус взглянул на часы в 5 часов 24 минуты.
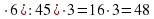 секунд.
секунд.
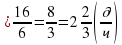 - производительность изготовления деталей
- производительность изготовления деталей  - производительность изготовления деталей
- производительность изготовления деталей 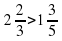 – производительность работы
– производительность работы 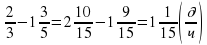 – выше скорость работы первого рабочего по отношению ко второму.
– выше скорость работы первого рабочего по отношению ко второму.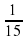 больше времени по сравнению с первым рабочим.
больше времени по сравнению с первым рабочим.



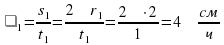 ;
;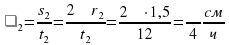 ;
;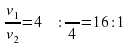 ;
;