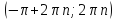Тригонометриялық теңсіздіктерді шешу

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Тригонометриялық теңсіздіктерді шешу»

Тригонометриялық теңсіздіктерді шешу

Мектеп бағдарламасында Тригонеметрия өте қызықты да, күрделі де, терең ойлау мен дұрыс әдіс тәсілдерді қолданатын тараулардың бірі. Теқ қана формуланы білу емес және қасиеттерді орынды пайдалану көптеген есептерді шешуде өз пайдасын тигізетіні бәрімізге мәлім. Тригонометриялық өрнектерді ықшамдау, түрлендіру; тригонометриялық теңдеулермен теңсіздіктерді шешу кейбір оқушыларға қиындықтар туғызады. Біріңғай Ұлттық тесттілеудің математика бөлімінде тригонометрияға кем дегенде үш есеп беріледі. Олар тригонометриялық өрнектерді ықшамдау, тригонометриялық теңдеу мен теңсіздікті шешу. Мектеп бағдарламасының оқу курсында осы аталған тақырыптар бойынша оқушылар терең түсіне алмағандықтан, дәл тест тапрсыру кезінде оқушылармыз қиналады.

Сондықтан, осы мақаламды математикаға қызығуы бар және тригонометрия бойынша білгісі келетін оқырмандармен аз да болса білгенімды қағаз бетіне түсіріп, бөліспекшімін.

Менің қарастыратын тақырыбым тригонометриялық теңсіздіктерді шешудің жолдары

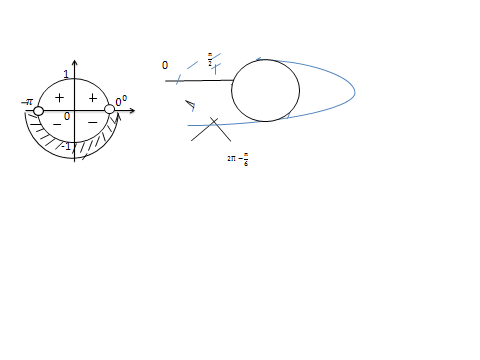
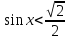1-мысал: теңсіздігін қарастырайық

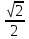Шешу: Алдыменен бірлік шеңбер сызып аламыз. Оған у = ге түзу жүргіземіз. Түзу сызып болған соң тиісті аралықты штрихтап алып жауабын жазамыз. Берілген теңсіздікті қанағаттандыраты аралық бірінші және екінші ширектерге орналасқан. Бұрыш оң мағынасы сағат тіліне қарама-қарсы бағытталғанын ескере отырып , төменгі жауапты аламыз.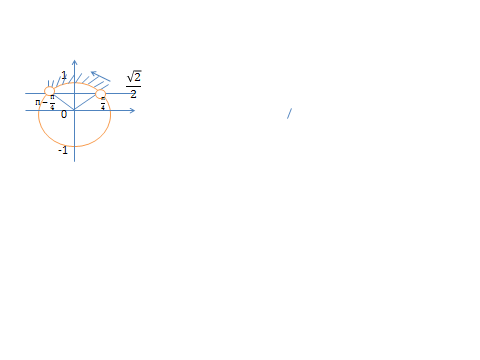

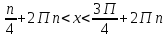
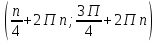
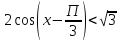Жауабы:

2 мысал: теңсіздігін шешіп көрейік.

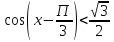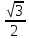Шешу: Теңсіздіктің екі жағын 2ге бөліп мына теңсіздікті аламыз, .

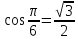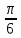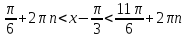
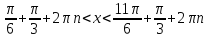
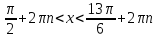
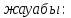
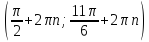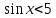
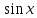Одан кейін бірлік шеңберімізді, х= түзуін сызып, тиісті аралықты штрихтап аламыз. Берілген сүретте теңсіздікті қанағаттандыратын аралықты көруге болады. Аралық басы бірінші ширекте, соғы төртінші ширекте. демек интервалдың бас нүктесінің бұрышы ға тең. Интервалдың соңын табу қиында емес. 360⁰ тан ны шигерсек қана жеткілікті.

3- мысал:

Шешу: Мұндай теңсіздіктерді шешу үшін у= функциясының мәндер жиынын ескеру керек. Бұл функия үшін -1 ден +1 ге дейінгі сандар мәндер облысын құрайды. Яғни функция 1ге тең және 1ден кіші бірақ -1ге тең және-1ден үлкен болады. 1ге тең және 1ден кіші фунция 5 саныдан да кіші болады. «Қай аралықта?» деген сұрақ туындаса, жауап бүкіл аралықта. Қорыта айтқанда 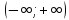жаубы болады.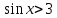

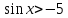
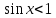
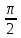4-мысал:

Шешу: бұл мысалды да шешу қиынға соқпайды. Өйткені алдыңғы мысалда айтылғандай мәндер облысын ескеру керек. Мәндер облысы 1 ден аспайтын функцияқалайша 3тен аса алады. Демек жауабы бос жиын яғни мұндай теңсіздік шешімі жоқ

5-мысал:

Шешу: Бұл теңсіздіктіңде шешімі барлық нақты сандар жиыны. Өйткені -1ге тең және -1ден үлкен сан әр дайым -5тен де үлкен болмақ. Сондықтан бұл теңсіздіктің шешімі болады.

6-мысал:

Шешу: Бұл теңсіздікті шешу үшін бірлік шеңбер сызу жеткілікті әрі түсінікті. У=1 түзуі сызып, барлық шешімдер түзудің төмен жағында орналасқанын жіне тек қана ден басқа бүкіл аралықты қамтығанын көруге болады.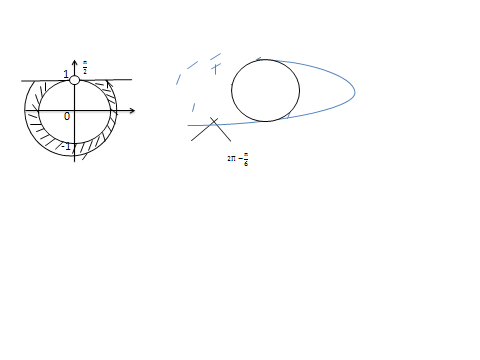

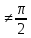
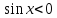Жауабы x

7-мысал: теңсіздігін шешіп көрейік

Бұл теңсіздікті шешу өте жеңіл. Жеңіл дегенімнің себебі, берілгін функция теріс мәндер қабылдайтын аралықты талап етіп отыр. Тригонометриялық функциялардың қасиеттерін ескере келе, яғни оның ішінде у= функциясы

ІІІ және IV ширек аралығында теріс мәндер қабылдайтынын білеміз.

Демек, жауабы

Еңбекшіқазақ ауданы Шелек ауылылы Т.Кенжебаев атындағы орта мектеп мектепке дейінгі шағын орталығымен коммуналдық мемлекеттік мекемесінің

математика пәнінің мұғалімі: Хизизахунов Нигмат

Предмет: Математика

Категория: Прочее

Целевая аудитория: 8 класс

Скачать
Тригонометриялық теңсіздіктерді шешу

Автор: Хизизахунов Нигматжан Именжанович

Дата: 12.04.2018

Номер свидетельства: 466015

Похожие файлы

Тригонометриялық теңсіздіктерді шешу

object(ArrayObject)#851 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(70) "Тригонометриялық теңсіздіктерді шешу"
    ["seo_title"] => string(45) "trighonomietriialyk_tien_sizdiktierdi_shieshu"
    ["file_id"] => string(6) "350720"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1476952070"
  }
}

?МЖ 10 сынып Алгебра. Тригонометриялы? те?сіздіктерді шешу

object(ArrayObject)#873 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(104) "?МЖ 10 сынып Алгебра. Тригонометриялы? те?сіздіктерді шешу"
    ["seo_title"] => string(62) "kmzh10synypalghiebratrighonomietriialyktiensizdiktierdishieshu"
    ["file_id"] => string(6) "268030"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1450527544"
  }
}

Тригонометриялы? те?сіздіктерді шешу

object(ArrayObject)#851 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(69) "Тригонометриялы? те?сіздіктерді шешу "
    ["seo_title"] => string(45) "trighonomietriialyk-tien-sizdiktierdi-shieshu"
    ["file_id"] => string(6) "159138"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(12) "planirovanie"
    ["date"] => string(10) "1421853727"
  }
}

Презентация Тригонометриялы? те?сіздіктерді шешу

object(ArrayObject)#873 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(92) "Презентация Тригонометриялы? те?сіздіктерді шешу "
    ["seo_title"] => string(61) "priezientatsiia-trighonomietriialyk-tien-sizdiktierdi-shieshu"
    ["file_id"] => string(6) "197318"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1428233488"
  }
}

Авторлық бағдарлама "Теңдеулер мен теңсіздіктерді шешу"

object(ArrayObject)#851 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(103) "Авторлық бағдарлама "Теңдеулер мен теңсіздіктерді шешу""
    ["seo_title"] => string(65) "avtorlyk_bag_darlama_tien_dieulier_mien_tien_sizdiktierdi_shieshu"
    ["file_id"] => string(6) "392290"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1487182682"
  }
}

Тригонометриялық теңсіздіктерді шешу

Просмотр содержимого документа «Тригонометриялық теңсіздіктерді шешу»

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Тригонометриялық теңсіздіктерді шешу»