Учитель математики МОУ СОШ №4 г. Краснослободска Пермякова Н.А.
Образовательные технологии обучения математике для реализации ФГОС общего образования
« Если мы будем учить сегодня так,
как мы учили вчера, мы украдем у детей завтра».
Джон Дьюи.
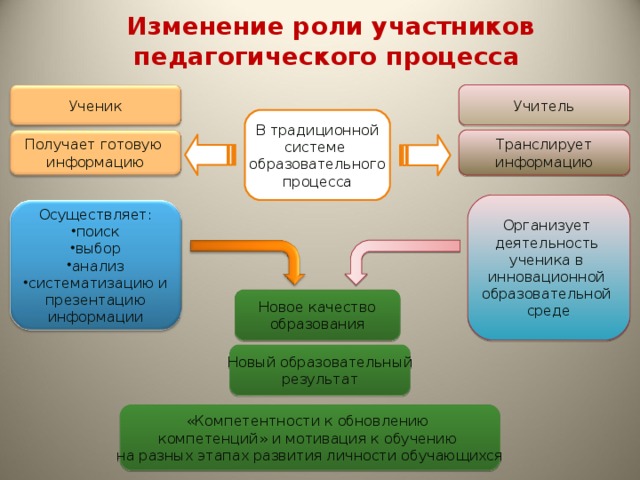
Особенность федеральных государственных образовательных стандартов общего образования - их деятельностный характер, который ставит главной задачей развитие личности ученика. Современное образование отказывается от традиционного представления результатов обучения в виде знаний, умений и навыков; формулировки ФГОС указывают на реальные виды деятельности.
Новые федеральные государственные образовательные стандарты второго поколения, отвечая требованиям времени и не растрачивая потенциала традиционной школы, смещают акцент на формирование у ученика личностных качеств созидателя и творца, его духовно-нравственное воспитание. Радикальные изменения происходят в
методах обучения (с объяснительного на деятельностный),
изменении оценки результатов обучения (оценка не только предметных ЗУН, но и метапредметных и личностных результатов),
изменении системы аттестации учителей (оценка качества управления учебной деятельностью учащихся),
изменении системы аттестации школ (оценка качества организации перехода школы к реализации ФГОС НОО).
Это говорит о том, что предстоит не формальный, а реальный переход школы к новой, гуманистической парадигме образования, дающее нашей стране шанс на будущее достойное существование и развитие.
В концепции ФГОС общего образования выделен культурно-исторический, системно - деятельностный подход к образованию учащихся. Поэтому наиболее эффективными будут те технологии, которые направлены на познание, коммуникативное, социальное и личностное развитие школьника.
В условия ФГОС хорошо вписываются известные педагогические технологии, проверенные в традиционной системе обучения и направленные на развитие ребенка, формирование у него компетенций, необходимых для приобретения знаний, жизненного опыта и социализации.
Информационно – коммуникационная технология
Технология развития критического мышления
Проектная технология
Технология проблемного обучения
Игровые технологии
Модульная технология
Технология мастерских
Кейс – технология
Остановимся кратко на 2-х педагогических технологиях.
Технология развития критического мышления
Что же такое критическое мышление?
КМ – под этим понятием подразумевается самостоятельное мышление, где отправной точкой является информация. Оно начинается от постановки вопросов, строится на основе убедительной аргументации.
Особенностью данной педагогической технологии является то, что учащийся в процессе обучения сам конструирует этот процесс, исходя из реальных и конкретных целей, сам отслеживает направления своего развития, сам определяет конечный результат. С другой стороны, использование данной стратегии ориентировано на развитие навыков вдумчивой работы с информацией, с текстом.
Определения КМ обычно включает в себя умение прогнозировать ситуацию, наблюдать, обобщать, сравнивать, выдвигать гипотезы и устанавливать связи, рассуждать по аналогии и выявлять причины, а также предполагает рациональный и творческий подход к рассмотрению любых вопросов.
Восприятие информации происходит в три этапа, что соответствует таким стадиям урока:
подготовительный – стадия вызова;
восприятие нового – смысловая стадия (или стадия реализации смысла);
присвоение информации – стадия рефлексии.
Формы урока в технологии развития критического мышления отличаются от уроков в традиционном обучении. Ученики не сидят пассивно, слушая учителя, а становятся главными действующими лицами урока. Они думают и вспоминают про себя, делятся рассуждениями друг с другом, читают, пишут, обсуждают прочитанное. Тексту отводится приоритетная роль: его читают, пересказывают, анализируют, трансформируют, интерпретируют, дискутируют, наконец, сочиняют.
Роль учителя — в основном координирующая.
В технологии критического мышления существует множество методических приемов для реализации целей разных фаз базовой модели урока.
Приемы обучения в технологии развития критического мышления
Прием «Таблицы» (таблица «Знаем –Хотим узнать- Узнаем», сводная таблица, концептуальная таблица)
Прием «Толстые и тонкие вопросы»
Прием «Инсерт»
Прием «Зигзаг»
Прием «Кластер»
Прием «Синквейн»
Приём «Таблицы»
Существует множество способов графической организации материала. Среди них самыми распространенными являются таблицы. Это таблица «Знаем-Хотим узнать – Узнаем», концептуальная таблица, сводная таблица.
(Презентация)
Таблица «Знаем – Хотим узнать – Узнаем» (З – Х – У)
З – знаем Х – хотим узнать У – узнаем
| З – что мы знаем | Х – что мы хотим узнать | У – что мы узнали, и что нам осталось узнать |
|
| | |
Учение начинается с активизации того, что дети уже знают по данной теме. Сначала нужно спросить, что они знают. Затем показать им картинку или предмет или обсудить с ними то, что знаю сама. Когда дети начнут предлагать свои идеи, выписать их на доску в первую колонку таблицы.
В колонку «Хочу узнать» можно внести свои спорные мысли и вопросы, возникшие в ходе обсуждения темы урока. Затем обучающиеся читают новый текст, пытаясь найти ответы на поставленные ими вопросы. После чтения текста ученикам предлагается заполнить колонку «Узнал». Располагаем ответы напротив поставленных вопросов. Далее обучающимся нужно предложить сравнить, что они знали раньше, с информацией, полученной из текста. При этом желательно излагать сведения, понятия или факты только своими словами, не цитируя учебник или иной текст, с которым работали. Например, при изучении тем «Сложение и вычитание дробей», «Четырёхугольники» можно составить такие таблицы (Презентация)
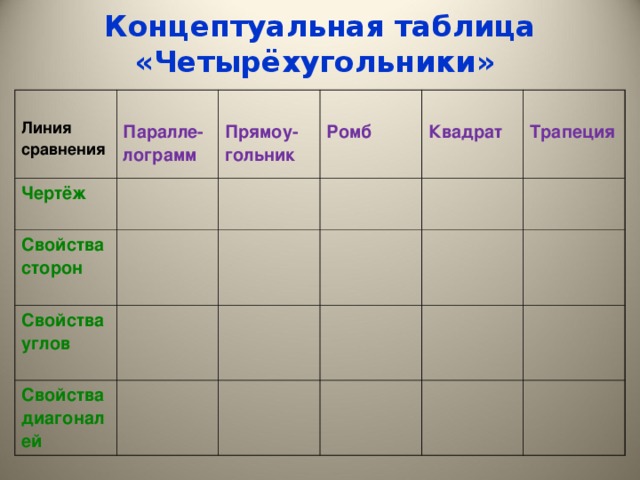
«Концептуальная таблица»
используется, когда необходимо провести сравнение нескольких объектов по нескольким вопросам. Таблица строится так: по горизонтали располагается то, что подлежит сравнению, а по вертикали различные черты и свойства, по которым это сравнение происходит. (Презентация)
В зависимости от цели, поставленной на уроке, таблица может заполняться учащимися на уроке или дома, постепенно или вся целиком как результат обобщения. Затем проводим обсуждение правильности заполненного материала, уточнение, дополнение, исправление; сравнение сил.
«Сводная таблица»
помогает систематизировать информацию, проводить параллели между явлениями, событиями или фактами. Выглядит эта таблица просто: Средняя колонка называется "линией сравнения". В ней перечислены те категории, по которым мы предполагаем сравнивать какие-то явления, события, факты. В колонки, расположенные по обе стороны от "линии сравнения", заносится информация, которую и предстоит сравнить. (Презентация)
Данные сравнительные таблицы помогают увидеть учащимся не только отличительные признаки объектов, но и позволяют быстрее и прочнее запоминать информацию. Составление сравнительных таблиц можно использовать как на стадии вызова, так и на стадии осмысления. На стадии вызова лучше всего попросить ребят заполнять ее карандашом, так как после работы с текстом у детей могут возникнуть исправления, которые выполняются ручкой. Общее лучше обводить красной ручкой.
Сводная таблица позволяет более качественно подготовить домашнее задание, так как является уже готовой памяткой, сделанной на уроке. При использовании приема "Сводная таблица" желательно, чтобы линий сравнения было не меньше трех, но и не больше шести. Такое количество позиций легче удержать в памяти. Нужно обязательно задавать вопросы тем, кто составлял таблицу. Эти вопросы должны быть интересны. Дети старших классов обязательно должны выделять линию сравнения сами, так как работать по навязанному сценарию не интересно. Гораздо интереснее опираться на то, что придумал сам. (Презентация)
Данная работа позволяет развивать у ребят помимо умения работы с текстом, следующие умения:
выделять ключевые слова;
систематизировать необходимую информацию;
анализировать, сравнивать и обобщать информацию;
развитие монологической речи;
а так же у ребят возникает потребность в поиске дополнительной информации, так как бывает, что не все вопросы охвачены на уроке. Эти вопросы и остаются в качестве домашнего задания, которое принимает форму увлекательной работы с информацией
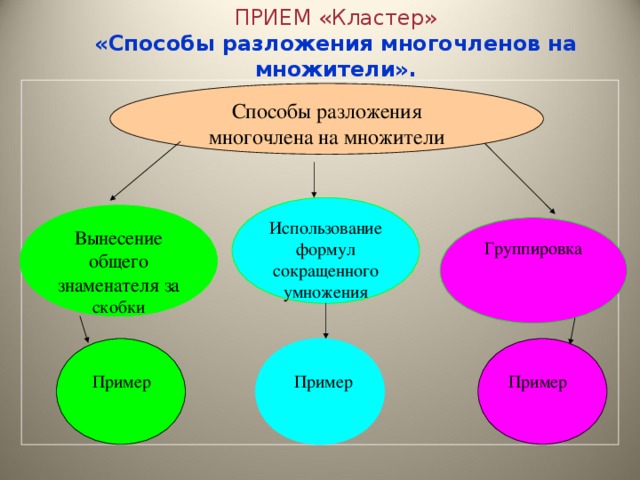
Прием «Составление кластера»
Кластер – прием систематизации материала в виде схемы (рисунка), когда выделяются смысловые единицы текста. Правила построения кластера очень простые. Рисуем модель Солнечной системы: звезду, планеты и их спутники. В центре располагается звезда – это наша тема. Вокруг нее планеты – крупные смысловые единицы. Соединяем их прямой линией со звездой. У каждой планеты свои спутники, у спутников свои. Система кластеров охватывает большое количество информации. (Презентация)
Прием "Кластеры" можно использовать как на стадии вызова, так и на стадии рефлексии, т.е. может быть способом мотивации к размышлению до изучения темы или формой систематизирования информации при подведении итогов.
(Презентация)
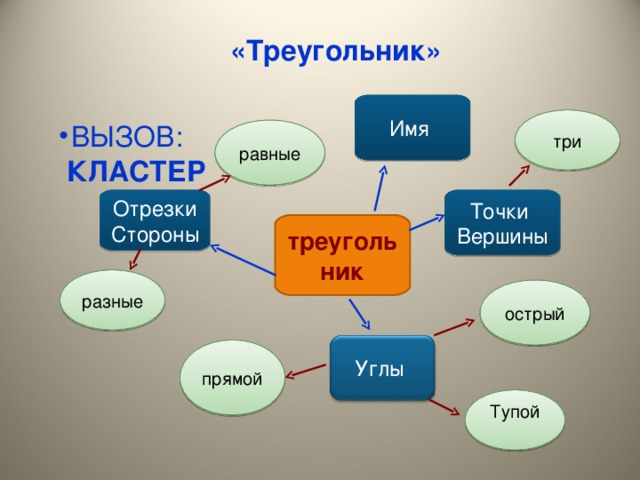
Например, задание: составьте кластер к слову «Треугольник». Обучающиеся выписывают все слова, которые у них ассоциируются с данным словом.
Сначала данную работу они выполняют самостоятельно, основываясь на тех знаниях, которые они имеют на начало урока. Затем читают параграф учебника «Треугольник» и продолжают работу по составлению кластера, это позволит сделать кластер более полным.
Этот прием развивает умение строить прогнозы и обосновывать их, учит искусству проводить аналогии, устанавливать связи, развивает навык одновременного рассмотрения нескольких вариантов, столь необходимый при решении жизненных проблем. Способствует развитию системного мышления. (Презентация).
Приём «Верные и неверные утверждения» или «Верите ли вы»
(Презентация)
Этот прием может быть началом урока. Учащиеся, выбирая "верные утверждения" из предложенных учителем, описывают заданную тему (ситуацию, обстановку, систему правил).
Затем просьба к учащимся установить, верны ли данные утверждения, обосновывая свой ответ. После знакомства с основной информацией (текст параграфа, лекция по данной теме) мы возвращаемся к данным утверждениям и просим учащихся оценить их достоверность, используя полученную на уроке информацию.
Приём «Толстые и тонкие вопросы»
Из жизненного опыта мы все знаем, что есть вопросы, на которые легко ответить "да" или "нет", но гораздо чаще встречаются вопросы, на которые нельзя ответить однозначно. Тем не менее, мы нередко оказываемся в ситуациях, когда человек, задающий вопросы, требует от него однозначного ответа.
Поэтому для более успешной адаптации во взрослой жизни детей необходимо учить различать те вопросы, на которые можно дать однозначный ответ (тонкие вопросы), и те, на которые ответить столь определенно не возможно (Толстые вопросы). Толстые вопросы – это проблемные вопросы, предполагающие неоднозначные ответы.
Для достижения цели на уроках необходимо использовать таблицу:
| ? | ? |
кто... что... когда... может... будет... мог ли... как звали... было ли... согласны ли вы... верно... | дайте объяснение, почему... почему вы думаете... почему вы считаете... в чем разница... предположите, что будет, если... что, если... |
Таблица "Толстых" и "Тонких" вопросов может быть использована на любой из трех стадий урока: на стадии вызова – это вопросы до изучения темы; на стадии осмысления – способ активной фиксации вопросов по ходу чтения, слушания; при размышлении – демонстрация пройденного.
. Работа по вопросам ведется в несколько этапов.
1 этап – учащиеся учатся по таблице задавать вопросы, записывая в таблице продолжение каждого вопроса. Сначала ребята сами придумывают "тонкие" вопросы, потом "толстые".
2 этап – учащиеся учатся записывать уже вопросы по тексту: сначала –"тонкие", а потом "толстые".
3 этап – при работе с текстом дети к каждой части записывают в каждую колонку таблицы по одному вопросу, которые после чтения задают своим товарищам.
Данная работа способствует развитию мышления и вниманию учащихся, а также развивается умение задавать ''умные'' вопросы. Классификация вопросов помогает в поиске ответов, заставляет вдумываться в текст и помогает лучше усвоить содержание текста.
Рекомендации по использованию толстых и тонких вопросов.
После того как дети заполнят таблицу, необходимо сразу же обсудить ее содержание. Чтобы работа с данным приемом принесла плоды, нужно осуществлять обратную связь – ребенок должен знать, как выполняют это задание его сверстники.
При обсуждении таблицы необходимо акцентировать внимание детей на том факте, что на толстые вопросы возможно несколько ответов, а на тонкие – только один.
Окончанием работы с этим приемом должна стать таблица ответов на толстые и тонкие вопросы. Эту таблицу ребята могут использовать при подготовке к проверочным работам.
Не все ученики одинаково легко заполняют таблицу. Не стоит настаивать – необходимо поощрять даже незначительные успехи.
При чтении текста можно разделить учеников на специалистов по тонким и толстым вопросам. Однако следует помнить, что тонкие вопросы задавать гораздо легче, поэтому нужно грамотно детей разделить на группы.
Приём Инсерт (insert)
(Презентация)
При чтении текста учащиеся на полях расставляют пометки (желательно карандашом).
Пометки должны быть следующие:
v если то, что вы читаете, соответствует тому, что вы знаете;
– если то, что вы читаете, противоречит тому, что вы уже знали;
+ если то, что вы читаете, является для вас новым;
? если то, что вы читаете, непонятно, или же вы хотели бы получить более подробные сведения по данному вопросу.
После чтения текста с маркировкой учащиеся заполняют маркировочную таблицу Инсерт, состоящую из 4-х колонок. Причём, заполняется сначала 1-я колонка по всему тексту, затем 2-я и т.д.
Прочитав учебный текст один раз, возвращаемся к своим первоначальным предположениям.
Следующим шагом может стать заполнение таблицы «Инсерт», количество граф которой соответствует числу значков маркировки:
| «V» – знаю | «+» – новое | «?» – вопросы |
| | | |
Этот прием работает и на стадии осмысления. Для заполнения таблицы ученикам понадобится вновь вернуться к тексту. Таким образом, обеспечивается вдумчивое, внимательное чтение. Технологический прием «Инсерт» и таблица «Инсерт» сделают зримым процесс накопления информации, путь от «старого» знания к «новому» – понятным и четким.
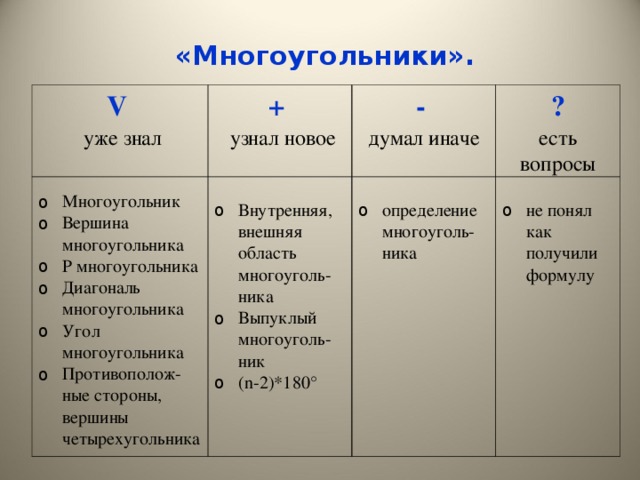
Такой прием можно использовать при изучении темы «Многоугольники» (Презентация)
На этапе рефлексии необходимо произвести обсуждение записей, внесенных в таблицу, или маркировки текста. Заканчивается работа озвучиванием таблицы, т.е. усвоенное знание проговаривается.
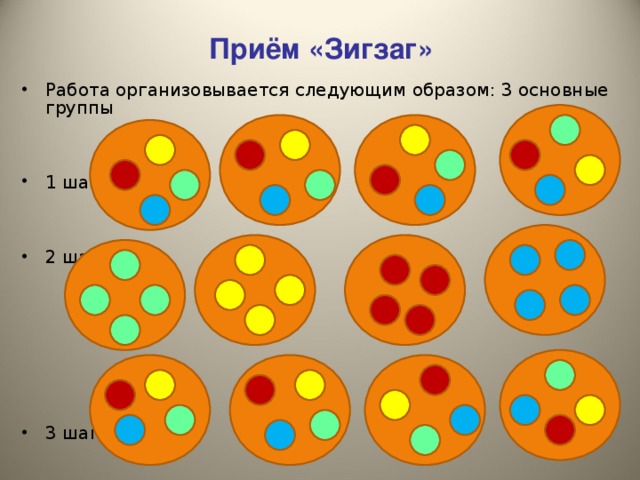
Прием «Зигзаг»
Класс разбивается на команды. Члену каждой команды присваивается номер 1,2,3,4,5 (зависит от количества текстов), заготавливаются таблички с соответствующими номерами на столы. На стадии вызова в ходе фронтальной беседы выясняется, выписывается на доску в кратко сформулированном виде то, что детям уже известно по данной теме.
Затем распределяются задания, каждый член группы получает свой объект исследования (свой вопрос для изучения). На столы выставляются номера, согласно которых происходит перегруппировка: все первые номера садятся вокруг стола с цифрой 1, вторые номера занимают места вокруг стола №2 и т.д. После изучения своего вопроса, составления кластера, оформления его на листе А4, ребята возвращаются в свои группы, происходит взаимообучение, т.е. обмен полученной информацией в группе. Сведения, поступившие от всех членов группы обсуждаются, оформляются в "Сводную таблицу".
Такая организация урока позволяет использовать разные виды деятельности, создать обстановку сотрудничества и сотворчества, что предотвращает утомление школьников, т.е. способствует здоровьесбережению.
Можно применять прием «Зигзаг» примере на уроке алгебры в 10 классе «Тригонометрические функции, их свойства и графики» (спаренные уроки).
Класс делится на 4-5 групп по 4 человека (число учеников в группах должно быть равно количеству текстов, предназначенных для изучения; в каждой рабочей группе должны быть учащиеся с разным уровнем знаний.
(Презентация)
Работа организовывается следующим образом: каждому ученику внутри группы предлагаю один из текстов о функциях y = sin x, y = cos x, y = tg x,
y=ctgx, их свойствах и графиках. Сначала ученики индивидуально знакомятся с теоретическим материалом, потом переходят в группы (их – 4 согласно текстам) и обсуждают основное содержание, выводы, которые посчитают нужными, записывают в тетради.
Далее ученики возвращаются в свои группы. Они ознакомились со своими текстами и теперь доносят до всей группы их содержание. Каждый участник группы записывает основное из всех четырех текстов. После этого группы готовятся к презентации всех четырех блоков теоретической информации.
Заключительный шаг – презентация. Все 4 группы по очереди представляют весь материал. Многократное разнообразное повторение теории позволяет каждому из присутствующих овладеть ею.
Во время презентаций учащиеся проверяют и дополняют записи в тетрадях. По итогам урока у каждого ученика в тетради получается конспект по изучаемой теме.
На этапе рефлексии учащиеся делятся впечатлениями о ходе урока, о своем вкладе в общий результат, о преимуществах или недостатках такой формы изучения нового материала.
Преимуществом стратегии «Зигзаг» является то, что за два урока каждым учеником, вне зависимости от его способностей, усваивается большой объем теоретического материала, всю работу на уроке учащиеся выполняют самостоятельно, сотрудничество и ответственность школьников за результат являются основными составляющими урока.
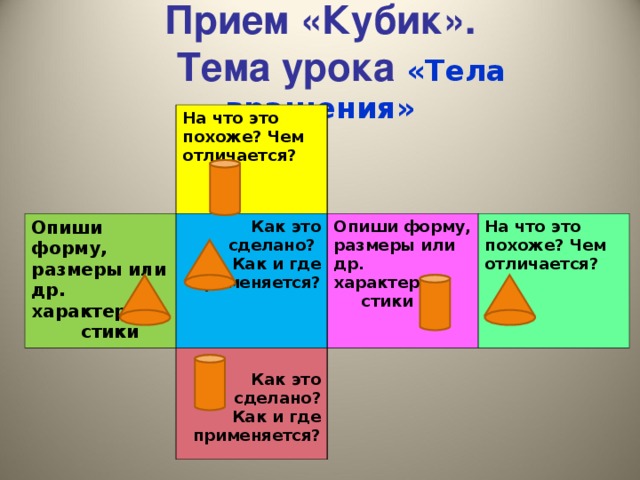
Прием «Кубик»
Данный прием используется на этапе осмысления. (Презентация)
Положительные стороны приема "Кубик":
– позволяет ученикам реализовать различные фокусы рассмотрения проблемы;
– создает на уроке целостное представление об изучаемом материале;
– создает условия для конструктивной интерпретации полученной информации.
Суть данного приема. Из плотной бумаги склеивается кубик. На каждой стороне пишется одно из следующих заданий:
1. Опиши это... (Опиши цвет, форму, размеры или другие характеристики)
2. Сравни это... (На что это похоже? Чем отличается?)
3. Проассоциируй это... (Что это напоминает?)
4. Проанализируй это... (Как это сделано? Из чего состоит?)
5. Примени это... (Что с этим можно делать? Как это применяется?)
6. Приведи "за" и "против" (Поддержи или опровергни это)
Ученики делятся на группы. Учитель бросает кубик над каждым столом и таким образом определяется, в каком ракурсе будет группа осмыслять ту или иную тему занятия. Учащиеся могут писать письменные эссе на свою тему, могут выступить с групповым сообщением и т.п. (Презентация)
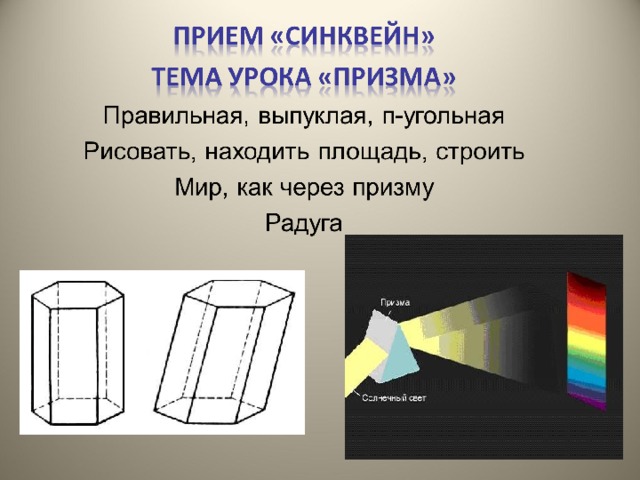
Приём «Синквейн»
это стихотворение, представляющее собой синтез информации в лаконичной форме, что позволяет описывать суть понятия или осуществлять рефлексию на основе полученных знаний”. (Презентация, слайд 17)
Слово происходит от французского “5”. Это стихотворение из 5 строк, которое строится по правилам:
1 строка – тема или предмет (одно существительное);
2 строка – описание предмета (два прилагательных);
3 строка – описание действия (три глагола);
4 строка – фраза из четырех слов, выражающая отношение к предмету;
5 строка – синоним, обобщающий или расширяющий смысл темы или предмета (одно слово).
Синквейн дает возможность подвести итог полученной информации, изложить сложные идеи, чувства и представления в нескольких словах. Прием «Синквейн» можно использовать при изучении тем «Призма», «Масштаб». (Презентация)
Кейс – технология
По сравнению с широко распространенными методами активного обучения школьников метод кейс-технологий не столь известен. Еще менее опробован он в применении к математике в школе, поскольку в отличие от гуманитарных дисциплин он предполагает разрешение участниками учебных групп проблемы, по своей сути, не имеющей однозначного решения.
Однако его преимущества: коллективный характер познавательной деятельности, творческий подход к познанию, сочетание теоретического знания и практических навыков столь привлекательны, что привлечение его к работе, даже при наличии трудностей в реализации методики в рамках школы имеет очень много плюсов.
Особенностью метода кейс - технологий является создание проблемной ситуации на основе фактов из реальной жизни. А что сейчас волнует многих школьников, изучающих математику в старших классах? Помимо проблемы итоговой аттестации возникают вопросы и сомнения, в коей мере приобретаемые в этой области знания могут и будут востребованы в дальнейшем, насколько оправданы как затраты времени, так и здоровья на изучение столь сложного предмета.
Виды кейсов: (презентация)
Печатный кейс (может содержать графики, таблицы, диаграммы, иллюстрации, что делает его более наглядным).
Мультимедиа кейс (наиболее популярный в последнее время, но зависит от технического оснащения школы).
Видео кейс (может содержать фильм, аудио и видео материалы). Его минусом является ограниченная возможность многократного просмотра, а значит, искажение информации и ошибки.
Типы кейсов: (презентация)
Практические кейсы. Реальные жизненные ситуации, детально и подробно отраженные. При этом их учебное назначение может сводиться к тренингу обучаемых, закреплению знаний, умений и навыков поведения (принятия решений) в данной ситуации. Кейсы должны быть максимально наглядными и детальными.
Научно-исследовательские кейсы. Они выступают моделями для получения нового знания о ситуации и поведения в ней. Обучающая функция сводится к исследовательским процедурам.
Обучающие кейсы. Отражают типовые ситуации, которые наиболее часты в жизни. Ситуация, проблема и сюжет здесь не реальные, а такие, какими они могут быть в жизни, не отражают жизнь «один к одному».
Примерная структура кейса:
Ситуация – случай, проблема, история из реальной жизни
Контекст ситуации - хронологический, исторический, контекст места, особенности действия или участников ситуации.
Комментарий ситуации, представленный автором
Вопросы или задания для работы с кейсом
Приложения
Организация работы учащихся на основе кейс-технологии.
Для проведения анализа конкретной ситуации работа с материалами кейса зависит от их объема, сложности проблематики и степени осведомленности обучаемых с данной информацией.
Возможны следующие альтернативные варианты:
Обучаемые изучают материалы кейса заранее, также знакомятся с рекомендованной преподавателем дополнительной литературой, часть заданий по работе с кейсом выполняется дома индивидуально каждым.
Обучаемые знакомятся заранее только с материалами кейса, часть заданий по работе с кейсом выполняется дома индивидуально каждым.
Обучаемые получают кейс непосредственно на занятии и работают с ним. Данный вариант подходит для небольших по объему кейсов, примерно на 1страницу.
Можно применить кейс-технологию на уроках геометрии при изучении раздела «Многогранники»
Кейс «Симметрия в пространстве»
Вид кейса: научно-исследовательский кейс
Тип кейса: исследовательский кейс
Класс делится на 2 группы, каждая группа получает кейс:
Группе 1 предлагается задача:
Сделайте вывод: «Разве во всём в жизни есть симметрия? И в архитектуре, и в строительстве, и в искусстве?»
Исследование проведите по схеме:
Возьмите для исследования объекты: дома на улице, здания церквей, дворцов, мост, картину, орнамент.
Рассмотрите выбранные объекты и ответьте на вопросы: обладают ли они симметрией? Если – нет, то почему? Если - да, то какой? Почему вы так решили?
Добавьте и исследуйте свой объект.
Исследование запишите в таблицу по форме:
Объект Обладают ли выбранные объекты симметрией (да/нет) Если - «да», то укажите вид симметрии, если - «нет», то укажите – почему вы так считаете. Опишите, в чем вы видите
сходство частей симметрии различие частей симметрии
Сфотографируйте ваши объекты (или скопируйте в интернете) и разместите их в презентации в программе PowerPoint.
Сделайте общие выводы:
Симметрична или асимметрична общая форма всех выбранных объектов?
Есть ли точное сходство в деталях?
Сделайте вывод о наличии симметрии в архитектуре, строительстве, искусстве. Используют ли люди в архитектуре, строительстве, искусстве понятие симметрии? Если да, то зачем? Если нет, то почему?
Группа 2
Задача. Докажите или опровергните слова: «Идею симметрии подсказывает сама природа».
Исследование проведите по схеме:
Возьмите для исследования объекты: овощ, фрукт, гриб, лист дерева, дерево, снежинку, птицу. Чтобы лучше рассмотреть детали некоторых объектов, воспользуйтесь лупой.
Рассмотрите выбранные объекты и ответьте на вопросы: обладают ли они симметрией? Если – нет, то почему? Если - да, то какой? Почему вы так решили?
Добавьте и исследуйте свои объекты – животное, насекомое, цветок.
Исследование запишите в таблицу по форме:
Объект Обладают ли выбранные объекты симметрией (да/нет) Если - «да», то укажите вид симметрии, если - «нет», то укажите – почему вы так считаете. Опишите, в чем вы видите
сходство частей симметрии различие частей симметрии
Сфотографируйте ваши объекты (или скопируйте в интернете) и разместите их в презентации в программе PowerPoint.
Сделайте общие выводы:
Симметрична или асимметрична общая форма всех выбранных объектов?
Есть ли точное сходство в деталях?
Сделайте вывод о наличии симметрии в природе: «Идею симметрии подсказывает сама природа» - верно ли это утверждение? Нужна ли живым организмам симметрия?