Школьный тур олимпиады по математике для учащихся 9 классов

Данная работа предназначена для учащихся 9 классов для отбора на муниципальный тур Всероссийской олимпиады школьников по математике. Целью такой работы является выявление одаренных, способных и увлеченных математикой детей, которые могут нестандартно мыслить, умеют выразить и записать свое решение.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Школьный тур олимпиады по математике для учащихся 9 классов»

Олимпиада, 9 класс, школьный тур

1) Может ли сумма шести различных положительных чисел равняться их произведению?

2) В связи с кризисом зарплата сотрудников фирмы понизилась на 1/5. На сколько процентов следует ее повысить, чтобы она достигла прежнего значения?

3) Чему равны острые углы прямоугольного треугольника, если угол между высотой и медианой, проведенными из вершины прямого угла, равен 26?

4) Докажите, что при любом справедливо числовое неравенство

5) Составьте квадратное уравнение, корни которого обратны квадратам корней уравнения

_______________________________________________________________________________________________________

Решение:

1) Может ли сумма шести различных положительных чисел равняться их произведению?

Например, возьмем первые 5 чисел равными 1,2,3,4,5. Шестое число найдем из уравнения:

Откуда, .

Ответ: Может.

Пусть до кризиса зарплата была равна х рублей. Тогда после кризиса зарплата стала 4/5х рублей. Чтобы зарплата достигла прежнего значения, ее надо увеличить в 5/4 раз, т.е. на одну четверть.

Ответ: на 25%.

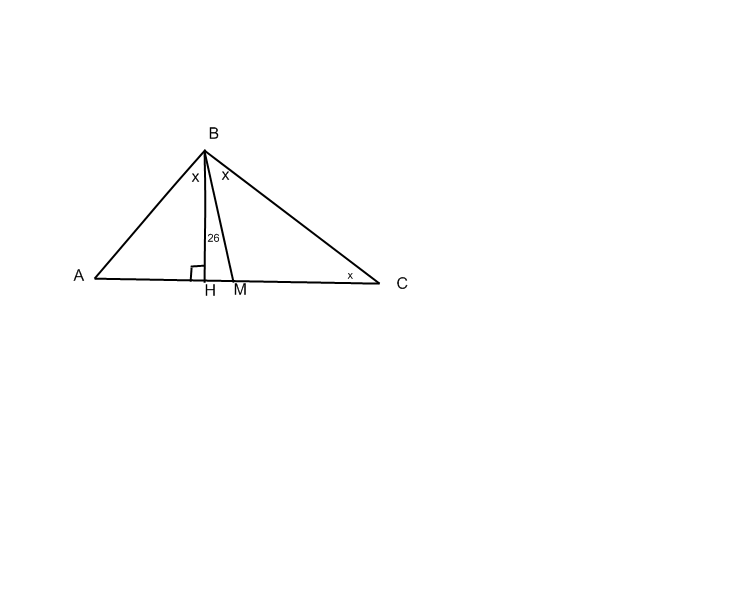ВН – высота, ВМ – медиана. Медиана равна половине гипотенузы, поэтому ВМ = МС, АВН = ВСМ = СВМ = х, 2х + 26= 90,

Х = 32, А = 58.

Ответ: А = 58, С = 32.

4) Докажите, что при любом справедливо числовое неравенство

Следовательно,

5) Составьте квадратное уравнение, корни которого обратны квадратам корней уравнения

Следовательно, . Тогда где

По условию , значит, .

Отсюда, .

Ответ:

Предмет: Математика

Категория: Прочее

Целевая аудитория: 9 класс

Скачать
Школьный тур олимпиады по математике для учащихся 9 классов

Автор: Накарякова Ольга Ивановна

Дата: 09.02.2015

Номер свидетельства: 169869

Похожие файлы

Школьный тур олимпиады по математике для учащихся 8 классов

object(ArrayObject)#852 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(109) "Школьный тур олимпиады по математике для учащихся 8 классов"
    ["seo_title"] => string(69) "shkol-nyi-tur-olimpiady-po-matiematikie-dlia-uchashchikhsia-8-klassov"
    ["file_id"] => string(6) "169908"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1423483497"
  }
}

программа работы с одаренными детьми по математике для 5-9 классов

object(ArrayObject)#874 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(121) "программа работы с одаренными детьми по математике для 5-9 классов "
    ["seo_title"] => string(72) "proghramma-raboty-s-odariennymi-diet-mi-po-matiematikie-dlia-5-9-klassov"
    ["file_id"] => string(6) "229138"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(12) "planirovanie"
    ["date"] => string(10) "1441628624"
  }
}

Олимпиадные задания для начальной школы

object(ArrayObject)#852 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(74) "Олимпиадные задания для начальной школы"
    ["seo_title"] => string(39) "olimpiadnyiezadaniiadlianachalnoishkoly"
    ["file_id"] => string(6) "309931"
    ["category_seo"] => string(16) "nachalniyeKlassi"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1458895347"
  }
}

Методические рекомендации к олимпиадным заданиям Всероссийской олимпиады школьников

object(ArrayObject)#874 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(160) "Методические рекомендации к олимпиадным заданиям Всероссийской олимпиады школьников "
    ["seo_title"] => string(93) "mietodichieskiie-riekomiendatsii-k-olimpiadnym-zadaniiam-vsierossiiskoi-olimpiady-shkol-nikov"
    ["file_id"] => string(6) "240273"
    ["category_seo"] => string(16) "nachalniyeKlassi"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1444984202"
  }
}

Олимпиадные задания по математике в 7 классе

object(ArrayObject)#852 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(81) "Олимпиадные задания по математике в 7 классе"
    ["seo_title"] => string(43) "olimpiadnyiezadaniiapomatiematikiev7klassie"
    ["file_id"] => string(6) "320350"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(12) "planirovanie"
    ["date"] => string(10) "1461065994"
  }
}

Школьный тур олимпиады по математике для учащихся 9 классов

Просмотр содержимого документа «Школьный тур олимпиады по математике для учащихся 9 классов»

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Школьный тур олимпиады по математике для учащихся 9 классов»