МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
КУДИНСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
Решение квадратных уравнений
разными способами
исследовательская работа по математике
Работу выполнила
ученица 8 класса:
Латышева Татьяна
руководитель: Кресюк
Светлана Викторовна
учитель математики
2014г
Содержание
Введение………………………………………………………………..3
Глава I.Виды квадратного уравнения…………………………………4
Глава II.Способы решения квадратных уравнений……………….....4
Применение свойств коэффициентов квадратного уравнения..4
Графический способ…………………………………………….5
Решение квадратных уравнений способом «переброски»
старшего коэффициента………………………………………….6
Решение квадратных уравнений с помощью
циркуля и линейки………………………………………………..7
Заключение……………………………………………………………...9
Приложения…………………………………………………………….10
Литература……………………………………………………………...15
Глава I. Введение
Кто хочет ограничиться настоящим без
знания прошлого, тот никогда его не поймет. Г.В. Лейбниц (немецкий математик XVII-XVIII веков)
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Актуальность темы:
Изучив решение квадратных уравнений, мне захотелось узнать можно ли еще другими способами решить уравнение и в дальнейшем использовать различные способы при решении уравнений.
Объект исследования: квадратные уравнения.
Предмет исследования: способы решения квадратного уравнения.
Цель работы: изучить способы решения квадратного уравнения, которые мы не изучаем на уроке. Научиться использовать эти способы.
Задачи: я поставила перед собой несколько задач. Решая эти задачи, я смогу раскрыть выбранную мною тему.
Понять, что называется квадратным уравнением.
Узнать какие виды квадратных уравнений существуют.
Найти информацию о способах решения квадратного уравнения и изучить её.
Решить уравнение разными способами и выяснить, какой способ удобен для решения этого уравнения.
Описание новизны и практической значимости: решение одного квадратного уравнения несколькими способами и выбрать более рациональный способ.
Структура данной работы следующая: введение
- в первой главе представлена виды квадратного уравнения;
- во второй главе- способы решения квадратных уравнений;
заключение;
приложения;
литература.
I Виды квадратного уравнения
Полное квадратное уравнение — алгебраическое уравнение общего вида
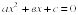
где х — свободная переменная, а, в, с — коэффициенты, причём а≠0
Выражение 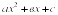 называют квадратным трёхчленом.
называют квадратным трёхчленом.
Корень — это значение переменной х, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в тождество.
Элементы квадратного уравнения имеют собственные названия:
а - называют первым или старшим коэффициентом,
в - называют вторым или коэффициентом при х,
с - называют свободным членом.
Неполные квадратные уравнения – это уравнение вида
ax2 = 0, где в=0 и с=0,
ax2 + bx = 0, где с=0
ax2 + c = 0, где коэффициент b=0
Приведенные квадратные уравнения – это уравнения вида x2 + px + q = 0, в котором старший коэффициент a=1, р – коэффициент при х (p = 
 ),
),
q – свободный член (q = 
 ).
).
II Способы решения квадратных уравнений
В 7-8 классах я изучила способы решения уравнения такие, как решение неполного квадратного уравнения, по формуле (нахождение дискриминанта), выделение квадрата разности и суммы, теорема Виета, решение квадратного уравнения с четным вторым коэффициентом. Эти способы я рассматриваю в приложении.
Следующие способы я нашла в интернете и покажу решение одного квадратного уравнения 3х2-8х+5=0.
Применение свойств коэффициентов квадратного уравнения
Этот метод в школе мы не рассматривали.
Пусть дано квадратное уравнение ах2 + вх + с = 0. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение. Согласно теореме Виета (приложение 5)
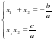
1. Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х1 = 1, х2 =  .
.
Доказательство. По условию а + b + с = 0, откуда b = – а – с. Значит,
Получаем х1 = 1, х2 =  .
.
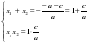
2. Если а - b + с = 0, или b = а + с, то х1 = – 1, х2 = –  .
.
Доказательство. По условию а – b + с = 0, откуда b = а + с. Таким образом,
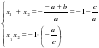
т.е. х1 = – 1 и х2 = –  , что и требовалось доказать
, что и требовалось доказать
Применим этот метод на примере 3х2-8х+5=0
найдем сумму коэффициентов: 3+(-8)+5=0
сумма равна нулю, значит х1=1, х2=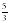
Вывод: этим способом можно решить только те уравнения, у которых сумма коэффициентов равна 1 или -1. Если сумма коэффициентов равна 1 или -1, то уравнение можно решить очень быстро и не допустить ошибок.
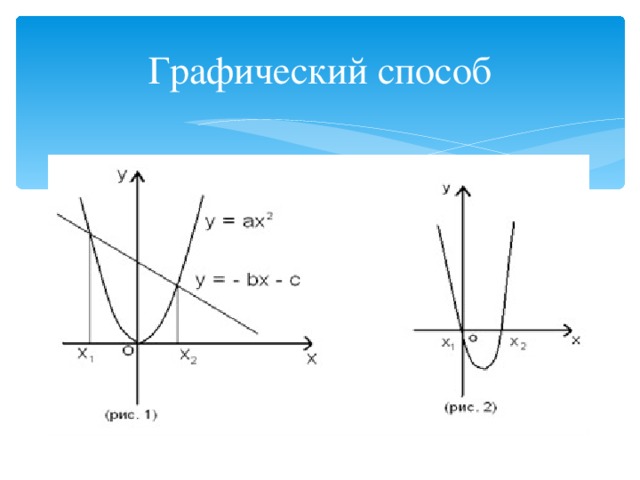
Графический способ
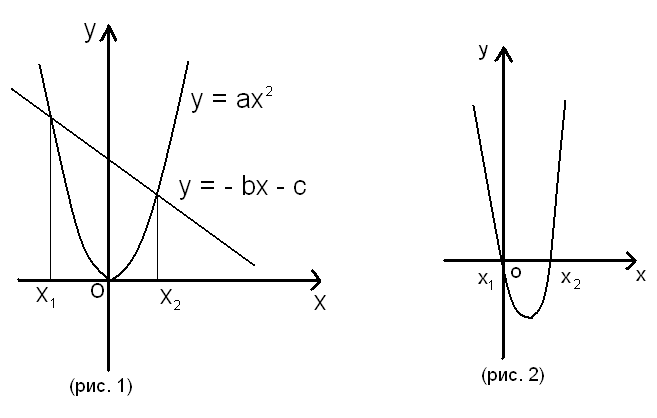
Квадратное уравнение можно решать и графическим способом. Решим графически уравнение ах2 + вx +с = 0. Оно равносильно уравнению
ах2 = - (вx + c). Постоим графики функций y = ax и y = - вx - c в одной системе координат (рис. 1). В точках х₁ и х₂ значения обеих функций равна. Следовательно, х₁ и х₂ являются корнями уравнения ах2 = - (bx + c) и равносильного ему уравнения ах2 + вx +с = 0
Если парабола и прямая пересекаются. То квадратное уравнение имеет два равных корня.
Если же парабола и прямая не пересекаются и не касаются, то квадратное уравнение не имеет корней.
Уравнение ах2 + вx +с = 0 можно решить иначе, построив параболу y = ах2 + bx +с и найдя точки ее пересечения с осью Ох, если D≥0 (рис. 2) (приложение 3)
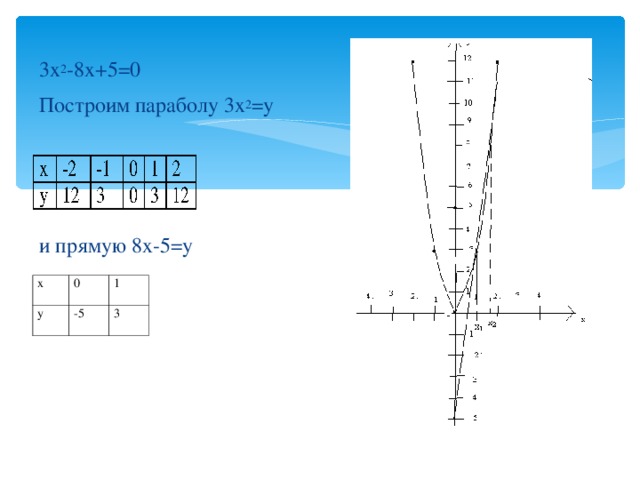
3х2-8х+5=0
Построим параболу 3х2=у и прямую 8х-5=у
Парабола: прямая:
| х | -2 | -1 | 0 | 1 | 2 |
| у | 12 | 3 | 0 | 3 | 12 |
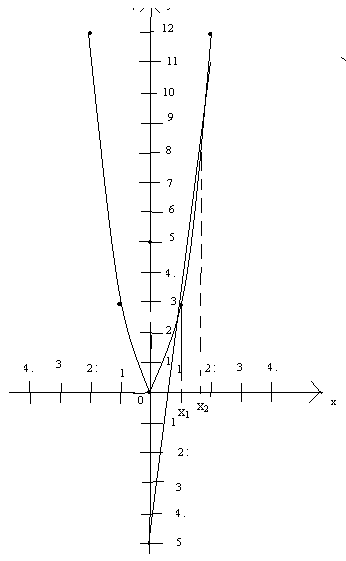
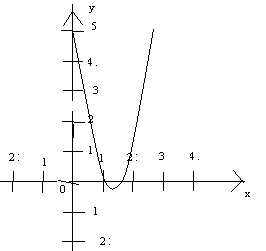
Рис 3 Рис 4
Точки пересечения прямой и параболы, т.е. их абсциссы и будут являться корнями уравнения (рис 3).
Можно построить параболу: 3х2-8х+5=0 и найти точки пересечения параболы и осью 0х.
Вершина параболы ( ;
;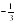 ). Рис 4
). Рис 4
Вывод: применяя графический метод не всегда можно найти точное значение корней. Поэтому этот метод часто применяют не для нахождения корней уравнения, а для определения их количества.
Решение квадратных уравнений способом «переброски» старшего коэффициента
Суть метода состоит в том, что корни квадратных уравнений
ax2 + bx + c = 0 и y2 + by + ac = 0 связаны соотношением: х =  .
.
Рассмотрим квадратное уравнение ax² + bx + c = 0, где a ≠ 0. Умножая обе его части на а, получаем уравнение а²х² + аbх + ас = 0. Пусть ах = у, откуда х =  ; тогда приходим к уравнению у² + bу + ас = 0, равносильному данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 =
; тогда приходим к уравнению у² + bу + ас = 0, равносильному данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = 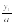 и х2 =
и х2 = 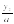 . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему. Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему. Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Уравнение: 3х2-8х+5=0
32х2-3*8х+3*5=0, обозначим 3х=у, отсюда х=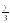
Получаем: у2-8у+15=0
По теореме Виета: у1+у2=8
у1*у2=15
теперь с легкостью можно подобрать корни уравнения: 3+5=8 и 3*5=15,
получается, что у1=3 и у2=5, теперь найдем х1 и х2: х1= =1 и х2=
=1 и х2=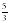 =
=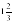
Вывод: Метод хорош для квадратных уравнений с “удобными” коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.
Решение квадратных уравнений с помощью циркуля и линейки
Проблема: по данным действительным коэффициентам a, b и c уравнения ax2 + bx +c = 0 определить радиус и координаты центра окружности, пересекающей ось ОХ в точках, абсциссы которых являются корнями данного уравнения.
Допустим, что искомая окружность пересекает ось абсцисс в точках
B (х1; 0) и C (х2; 0), где х1 и х2 – корни уравнения ах2 + bх + с = 0, и проходит через точки А (0; 1) и E (0; ) на оси ординат. Тогда по теореме о секущихся имеем ОВ ∙ ОС = ОА ∙ ОЕ, откуда ОЕ = 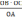 =
=  .
.
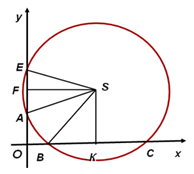
Центр окружности находиться в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
SK = 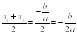 ; SF =
; SF =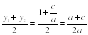 .
.
Итак:
1. Выберем систему координат.
2. Построим точки S(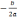 ;
;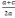 ) (центр окружности) и А (0;1).
) (центр окружности) и А (0;1).
3. Проведем окружность с радиусом SA.
4. Абсциссы точек пересечения этой окружности с осью ОХ являются корнями квадратного уравнения.
При этом возможны три случая:
1. Радиус окружности больше ординаты центра (SА SВ), окружность пересекает ось ОХ в двух точках B (х1; 0) и D (х2; 0), где х1 и х2 – корни квадратного уравнения (рис.1).
2. Радиус окружности равен ординате центра (SА = SВ), окружность касается оси ОХ в точке B (х1; 0), где х1 – корень квадратного уравнения (рис.2).
3. Радиус окружности меньше ординаты центра (SА
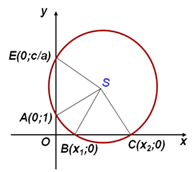


рис. 1 рис. 2 рис. 3
Уравнение: 3х2-8х+5=0
Центр окружности: S(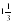 ;
;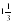 )
)
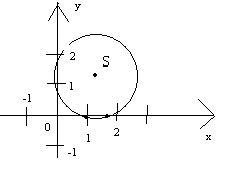
Окружность пересекается с осью 0х в точках с абсциссой 1 и 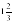 .
.
Вывод: с помощью этого способа решения квадратного уравнения легко провести исследование его корней на знак. Но, очевидно, что этот красивый способ практически не применяется из-за геометрических построений и последующей проверки результатов решения.
Я рассмотрела 4 новых для себя способа решения квадратных уравнений и 5 способов изученных в школе, решила уравнение 3х2-8х+5=0 семи способами. Каждый способ по своему хорош, но для моего выбранного уравнения удобный способ решения это применение свойств коэффициентов квадратного уравнения, так как вычислив сумму коэффициентов, получаем в результате 0, следовательно, первый корень равен 1, а второй - 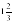 .
.
Заключение
Квадратные уравнения находят широкое применение при решении задач различного уровня сложности. Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.
В своей работе я проводила исследование способов решения квадратных уравнений и составила справочный материал для своих одноклассников (приложение 6). В результате выполнения работы были изучены следующие способы:
Применение свойств коэффициентов квадратного уравнения
Графический способ
Решение квадратных уравнений способом «переброски» старшего коэффициента
Решение квадратных уравнений с помощью циркуля и линейки
Решение неполного квадратного уравнения (приложение 1)
Метод выделения полного квадрата (приложение 2)
Решение квадратных уравнений по формуле(приложение 3)
Решение квадратного уравнения с четным вторым коэффициентом (приложение 4)
Теорема Виета (приложение 5)
Подводя итоги можно сказать, что каждый из изученных способов имеет как положительные стороны, так и недостатки. Но выполненная работа показывает, что использование различных способов при решении квадратных уравнений является важным звеном в изучении математики, развивает внимание и сообразительность. Так же не менее важно умение правильно выбирать рациональный способ решения конкретно для каждого уравнения.
Я считаю эту тему актуальной, так как она может пригодиться нам не только во время обучения в школе, а в последующем и в ВУЗе, но и на протяжении всей жизни.
Приложение 1
Решение неполного квадратного уравнения
| № | Вид уравнения | Решение | Корни уравнения |
| 1 | ах2 + с = 0
| Равенство требует, чтобы квадрат неизвестного равнялся количеству, это возможно только тогда, когда количество есть положительное число т.е. с и а имеют противоположные знаки. Уравнение будет иметь два корня. Если числа с и а имеют одинаковые знаки, то количество представляет собой отрицательное число; тогда уравнение не может быть удовлетворено никаким вещественным числом; в этом случае говорят, что уравнение имеет два мнимых корня. | x1 = 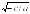 x2 = -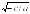
|
| 2 | ах2 + bx = 0 х(ax +b)=0 | Произведение может равняться нулю только тогда, когда какой – нибудь из сомножителей равен нулю, а второй при этом имеет смысл; следовательно, рассматриваемое уравнение удовлетворяется, если положим, что х =0 или ах +b = 0 | x1 = 0 и x2 = -b/a |
| 3 | ax2 = 0 | квадратное уравнение ax2 = 0 имеет очевидно, только одно решение | х = 0.
|
Изучение решения квадратных уравнений происходит в школьном курсе математике 8 класса, но изучая тему в 7 классе: «Вынесение общего множителя за скобки», мы встречались с уравнениями вида ах2 + bx = 0.
Например, №661(г) (учебник 7 класса)
3х2-1,2х=0
х=0 или х=1,2
Ответ х=0 и х=1,2
Также в 7 классе, изучали тему : «Формулы сокращенного умножения », решали уравнения вида ах2 + с = 0.
Например № 890(з) (учебник 7 класса)
25х2-16=0
(5х-4)(5х+4)=0
(5х-4)=0 или (5х+4)=0
х1=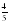 и х2=-
и х2=-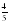
Ответ: х1=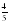 и х2=-
и х2=-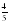
Вывод: решение неполных квадратных удобен, в том, что не нужно применять формулы по которым решают квадратные уравнения, а просто привести множители к виду линейного уравнения.
Приложение 2
Метод выделения полного квадрата
Цель - привести уравнение общего вида к неполному квадратному уравнению. В этом нам помогут формулы сокращенного умножения, а именно, квадратов суммы и разности:
(а + b)2 = a2 + 2ab + b2; (a – b)2 = a2 – 2ab + b2.
Поясним этот метод на примере.
Пример
4х2+12х+9=0
(2х+3)2=0
(2х+3)(2х+3)=0
(2х+3)=0 или (2х+3)=0
х=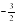 уравнение имеет два одинаковых корня.
уравнение имеет два одинаковых корня.
Ответ: х=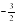
Вывод: Этот метод применим для любых квадратных уравнений, но не всегда удобен в использовании, так как часто приводит к громоздким преобразованиям. Поэтому поступают иначе. Решают уравнение в общем виде и в результате получают формулу корней. Затем эту формулу применяют при решении любого квадратного уравнения.
Приложение 3
Решение квадратных уравнений по формуле
Решим квадратное уравнение
aх2 +bx + c = 0 (1)
Разделив обе части на а, получим равносильное ему приведенное квадратное уравнений

Преобразуем это уравнение:

 (2)
(2)
Уравнение (2) равносильно уравнению (1). Число его корней зависит от знака дроби  . Так как а≠0, то 4а2 – положительное число, поэтому знак этой дроби определяется знаком ее числителя, т.е. выражения b2 – 4ac. Это выражение называют дискриминантом квадратного уравнения aх2 +bx + c = 0 («дискриминант» по латыни - различитель). Его обозначают буквой D, т.е.
. Так как а≠0, то 4а2 – положительное число, поэтому знак этой дроби определяется знаком ее числителя, т.е. выражения b2 – 4ac. Это выражение называют дискриминантом квадратного уравнения aх2 +bx + c = 0 («дискриминант» по латыни - различитель). Его обозначают буквой D, т.е.
D = b2 – 4ac.
Запишем уравнение (2) в виде
 .
.
Рассмотрим теперь различные возможные случаи в зависимости от D.
Если D0, то
 или
или 
Таким образом, в этом случае уравнение (1) имеет два корня
Принята следующая краткая запись:
 , где D = b2 – 4ac, (I)
, где D = b2 – 4ac, (I)
которую называют формулой корней квадратного уравнения
Если D=0, то уравнение будет иметь 1 корень: 
Если D, то значение дроби  отрицательно и поэтому уравнение не имеет корней.
отрицательно и поэтому уравнение не имеет корней.
Пример № 541(б) из учебника 8 класса
3х2-8х+5=0
D=64-4*3*5=40
х1= ; х2=
; х2=
Ответ: х1=1; х2=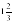
Вывод: с помощью формулы можно решить любое квадратное уравнение.
Приложение 4
Решение квадратного уравнения с четным вторым коэффициентом.
ах2+2kх+с=0, где в=2k
Найдем его дискриминант: D=4k2-4ас=4(k2-ас). Очевидно, что число корней уравнения зависит от знака выражения k2-ас. Обозначим это выражение через D1.
Если D1≥0, то по формуле корней квадратного уравнения получим
 , где D1= k2-ас
, где D1= k2-ас
Для примера я хочу показать то же уравнение, что и в предыдущем методе.
3х2-8х+5=0
D1=16-3*5=1
х1= и х2=
и х2=
Ответ: х1=1; х2=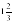
Вывод: для вычисления используются числа меньше, чем при вычислении с помощью дискриминанта, поэтому чаще всего вычислительные ошибки не допускают. Этот способ не всегда применим, только тогда когда второй коэффициент четный
Приложение 5
Теорема Виета
Теорема: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
x2+px+q=0
D=p2-4q
x1= и x2=
и x2=
найдем сумму и произведение корней:
х1+х2=  +
+ =
=
х1*х2=  *
* =
=
Итак,
Теорема доказана.
Рассмотрим этот метод на примере
3х2-8х+5=0
Представим уравнение в виде приведенного, разделив левую часть на 3:

По теореме Виета:
х1+х2= 1+
1+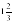 =
=
х1*х2=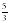 1*
1*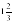 =
=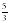
Ответ: х1=1; х2=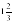
Вывод: удобен этот способ в том, что можно решить уравнение устно. Сложность, в том, что не всегда можно подобрать корни уравнения, так как корни могут быть рациональными и иррациональными числами.
Приложение 6
Способы решения квадратных уравнений
1 неполные квадратные уравнения
| № | Вид уравнения | Решение | Корни уравнения |
| 1 | ах2 + с = 0
| ах2 = с | x1 = 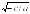 ; x2 = - ; x2 = -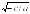
|
| 2 | ах2 + bx = 0 | х(ax +b)=0 | x1 = 0 и x2 = -b/a |
| 3 | ax2 = 0 | x2 = 0 | х = 0.
|
2 решение по формуле: ах2+вх+с=0
D = b2 – 4ac, 
| Если D0 (2 корня) | Если D=0 (1 корень) | Если D0 (нет корней) |
|  ; ; 
| 
| - |
3 Решение квадратного уравнения с четным вторым коэффициентом.
ах2+2kх+с=0, где в=2k
D1= k2-ас , 
4 теорема Виета, приведённое квадратное уравнение, где а=1
x2+px+q=0 ,
5 Применение свойств коэффициентов квадратного уравнения
- если а + b + с = 0, то х1 = 1, х2 = .
.
- если а - b + с = 0, или b = а + с, то х1 = – 1, х2 = –  .
.
6 Решение квадратных уравнений с помощью циркуля и линейки
1. Выберем систему координат.
2. Построим точки S(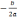 ;
;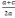 ) (центр окружности) и А (0;1).
) (центр окружности) и А (0;1).
3. Проведем окружность с радиусом SA.
4. Абсциссы точек пересечения этой окружности с осью ОХ являются корнями квадратного уравнения.
7 Графический способ
| | Уравнение ах2 + вx +с = 0 можно решить графическим способом, построив параболу y = ах2 + bx +с и найдя точки ее пересечения с осью Ох, если D≥0 |
8 Решение квадратных уравнений способом «переброски» старшего коэффициента
ax2 + bx + c = 0 умножим все коэффициенты на а, обозначим у=ха (х =  ) получаем: y2 + by + ac = 0 (решить уравнение и вернуться к переменной х)
) получаем: y2 + by + ac = 0 (решить уравнение и вернуться к переменной х)
Литература
Алгебра. 7 класс. Учеб. Для общеобразоват. учреждений /Макарычев Ю.Н. и др./ под ред. С.А.Телековского.- М.:Просвещение, 2009г.
Алгебра. 8 класс. Учеб. Для общеобразоват. учреждений /Макарычев Ю.Н. и др./ под ред. С.А.Телековского.- М.:Просвещение, 2009г.
Алгебра. 9 класс. Учеб. Для общеобразоват. учреждений /Макарычев Ю.Н. и др./ под ред. С.А.Телековского.- М.:Просвещение, 2009г.
Дроздов В. Квадратное уравнение: варианты решения. Математика // Приложение к газете «Первое сентября» №10/1997. стр.6.
Информация про квадратные уравнения http://ru.wikipedia.org/wiki/
6. Панкратова Л. Квадратные уравнения. Математика // Приложение к газете «Первое сентября» №21/1996. стр.5-6.
7. Плужников И. Десять способов решения квадратных уравнений. Математика // Приложение к газете «Первое сентября» №40/2000. стр.24 -31.
ОТЗЫВ
на исследовательскую работу:
«Решение квадратных уравнений разными способами»
Латышевой Татьяны 8 класса
Работа состоит из введения, двух глав, заключения и приложений. Во введении показана актуальность данной темы. В первой главе Таня рассматривает три вида квадратных уравнений. Во второй главе, показывает решение уравнения различными способами и делает вывод. В заключительной части работы подводит итоги изучения темы, формулирует выводы и предложения.
Исследовательская работа Латышевой Татьяны посвящена изучению решения квадратных уравнений разными способами.
В представленной работе Татьяна ставила перед собой цель и несколько задач. Целью является изучение способов решения квадратного уравнения, которые не изучают на уроке и научиться использовать рационально эти способы. Решая поставленные задачи, Татьяна подробно рассмотрела три вида квадратных уравнений, четыре способа решений, которые не рассматриваются в школьном курсе математике. Также было выбрано одно уравнение из учебника «алгебра 8 класса» и показано решение каждым способом. Основные, изученные в школе, способы представлены в приложении.
В работе можно отметить, что Таня проявила умение разобраться в различных способах решения с помощью изучения дополнительной литературы и самостоятельно решить уравнение. Татьяна, безусловно, углубляет наше представление о решении квадратных уравнений и призывает своих одноклассников использовать рационально эти способы с помощью справочного материала, который представлен в приложении 6.
Работу можно продолжить: изучить еще способы решения квадратных уравнений; изучить историю возникновения и развития квадратных уравнений; составить сборник задач на каждый изученный способ.
Работа может быть оценена положительно.
Дата Руководитель (подпись)
(слайд 1) Решение квадратных уравнений
разными способами
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
(слайд 2) Актуальность темы:
Изучив решение квадратных уравнений, мне захотелось узнать можно ли еще другими способами решить уравнение и в дальнейшем использовать различные способы при решении уравнений.
Цель работы: изучить способы решения квадратного уравнения, которые мы не изучаем на уроке. Научиться использовать эти способы.
(слайд 3) Объект исследования: квадратные уравнения.
Предмет исследования: способы решения квадратного уравнения.
(слайд 4) Задачи: я поставила перед собой несколько задач. Решая эти задачи, я смогу раскрыть выбранную мною тему.
Понять, что называется квадратным уравнением.
Узнать какие виды квадратных уравнений существуют.
Найти информацию о способах решения квадратного уравнения и изучить её.
Решить уравнение разными способами и выяснить, какой способ удобен для решения этого уравнения.
Новизна в мое работе - решение одного квадратного уравнения несколькими способами и выбрать более рациональный способ.
(слайд 5) I Виды квадратного уравнения
- Полное квадратное уравнение — алгебраическое уравнение общего вида
- Неполные квадратные уравнения – это уравнение вида
ax2 = 0, где в=0 и с=0,
ax2 + bx = 0, где с=0
ax2 + c = 0, где коэффициент b=0
- Приведенные квадратные уравнения – это уравнения вида x2 + px + q = 0,
(Слайд 6) Способы решения квадратных уравнений изученные в школе
1 Решение неполного квадратного уравнения
2 Метод выделения полного квадрата
3 Решение квадратных уравнений по формуле
4 Решение квадратного уравнения с четным вторым коэффициентом
5 Теорема Виета
(слайд 7) Следующие способы я нашла в интернете и покажу решение одного квадратного уравнения 3х2-8х+5=0.
(слайд 8) Этот способ заключается в том чтобы проверить сумму коэффициентов, если сумма равна 1, то х1 = 1, х2 =  . Если сумма равна – 1, то х1 = – 1 и х2 = –
. Если сумма равна – 1, то х1 = – 1 и х2 = – 
(Слайд 9) Вывод: этим способом можно решить только те уравнения, у которых сумма коэффициентов равна 1 или -1. Если сумма коэффициентов равна 1 или -1, то уравнение можно решить очень быстро и не допустить ошибок.
(Слайд 10) Графический способ заключается в следующем: построить графики
y = ax и y = - вx - c в одной системе координат и найти абсциссы точек пересечения (рис 1). Можно решить иначе, построив параболу y = ах2 + bx +с и найдя точки ее пересечения с осью Ох, если D≥0(рис 2).
(Слайд 11) Пример
Вывод: применяя графический метод не всегда можно найти точное значение корней. Поэтому этот метод часто применяют не для нахождения корней уравнения, а для определения их количества.
(Слайд 12) Вывод: Метод хорош для квадратных уравнений с “удобными” коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.
(Слайд13) Решение квадратных уравнений с помощью циркуля и линейки. Решение в 4 этапа.
(Слайд 14) Пример
Вывод: с помощью этого способа решения квадратного уравнения легко провести исследование его корней на знак. Но, очевидно, что этот красивый способ практически не применяется из-за геометрических построений и последующей проверки результатов решения.
Каждый способ по своему хорош, но для моего выбранного уравнения удобный способ решения это применение свойств коэффициентов квадратного уравнения, так как вычислив сумму коэффициентов, получаем в результате 0, следовательно, первый корень равен 1, а второй -  .
.
(Слайд 15) А в заключении хотелось бы сказать, что каждый из изученных способов имеет как положительные стороны, так и недостатки. Но выполненная работа показывает, что использование различных способов при решении квадратных уравнений является важным звеном в изучении математики, развивает внимание и сообразительность. Так же не менее важно умение правильно выбирать рациональный способ решения конкретно для каждого уравнения.
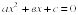
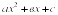 называют квадратным трёхчленом.
называют квадратным трёхчленом.
 ),
), 
 ).
). 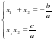

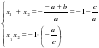
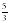



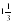 ;
;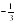 ). Рис 4
). Рис 4 .
.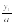 и х2 =
и х2 = 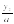 . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему. Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему. Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.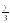
 =1 и х2=
=1 и х2=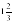
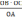 =
=  .
.
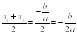 ; SF =
; SF =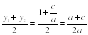 .
.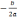 ;
;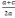 ) (центр окружности) и А (0;1).
) (центр окружности) и А (0;1). 



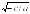
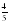 и х2=-
и х2=-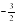 уравнение имеет два одинаковых корня.
уравнение имеет два одинаковых корня.