ГУ Осьмерыжская основная общеобразовательная школа
Невозможные фигуры
Направление: физико-математическое

Исполнитель работы: Диппель Сергей ученик 6 класса Осьмерыжской ООШ Павлодарская область Качирский район село Осьмерыжск
Руководитель работы: Довженко Наталья Владимировна учитель математики Осьмерыжской ООШ


2013 год
Оглавление.
Резюме /аннотация/………………………………………………………………2
Введение……………………………………………………………………..........3
1. Немного из истории ……………………………………………..………….5
2. Виды невозможных фигур…………….…………………………………….9
3. Оскар Рутерсвард – отец невозможной фигуры……….…………………..16
4. Невозможные фигуры - возможны!………………………………………...18 5. Применение невозможных фигур……………………………………..……19
Заключение…………………………………………………………………….....21
Список литературы………………………………………………………………22
Резюме /аннотация/
Этапы проекта:
1 этап.
Постановка проблемы, постановка целей, задач информационно-исследовательской работы;
Проведение бесед о невозможных фигурах;
Постановка проблемного вопроса, мотивация к реализации проекта;
Проведение предварительной работы по теме «Невозможные фигуры»;
Обсуждение и составление поэтапного плана работы, создание банка идей и предложений. Выбор источников информации.
2 этап. Деятельность по реализации проекта.
Информационно-образовательные беседы;
Информационно-поисковая работа;
Экспериментальная работа;
Обзор литературы
Достижение целей
Введение
С некоторых пор меня заинтересовали такие фигуры, которые на первый взгляд кажутся обычными, а присмотревшись можно увидеть, что что-то в них не так. Основной интерес для меня представляли так называемые невозможные фигуры, посмотрев на которые создается впечатление, что существовать в реальном мире они не могут. Я захотел узнать о них больше.
Несмотря на то, что невозможные фигуры известны чуть ли не со времен наскальной живописи, их систематическое изучение началось лишь в середине XX века, то есть практически на наших глазах, а до этого математики отмахивались от них как от досадного недоразумения.
В 1934 году Оскар Реутерсвард (Oscar Reutersvard) случайно создал свою первую невозможную фигуру - треугольник, составленный из девяти кубиков, но вместо того, чтобы что-то исправить, принялся создавать другие невозможные фигуры одну за другой.
Даже такие простые объемные формы, как куб, пирамида, параллелепипед можно представить как комбинацию нескольких фигур, находящихся на разном расстоянии от глаза наблюдателя. Всегда при этом должна быть линия, по которой изображение отдельных частей совмещающих в целостную картину.
«Невозможная фигура - это выполненный на бумаге трехмерный объект, который не может существовать в действительности, но который, однако, можно видеть как двухмерное изображение». Это один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия невозможности существования такой фигуры в трёхмерном пространстве.
Несмотря на значительное количество публикаций о невозможных фигурах их четкого определения по существу не сформулировано. Можно прочесть, что к невозможным фигурам относятся все оптические иллюзии, связанные с особенностями нашего восприятия мира. С другой стороны человек может показать Вам фигуру человека зеленого цвета или с десятью руками и пятью головами и сказать, что все это невозможные фигуры. При этом он будет по своему прав. Ведь людей зеленого цвета с десятью ногами не бывает. По этому мы под невозможными фигурами будем пониматься плоские изображения фигур воспринимаемые человеком однозначно, как они нарисованы без восприятия человеком каких бы то ни было дополнительных, фактически не нарисованных изображений или искажений и которые не возможно представить в трехмерном виде. Невозможность представления в трехмерном виде понимается, конечно, только непосредственная без учета возможности применения специальных средств при изготовлении невозможных фигур, т. к. всегда невозможную фигуру можно изготовить, применив хитроумную систему прорезей, дополнительных поддерживающих элементов и изгибания элементов фигуры, а затем сфотографировав ее под нужным углом
Передо мной встал вопрос: «Существуют ли в реальном мире невозможные фигуры?»
Цели проекта:
1.Выяснить, как создаются нереальные фигуры.
2. Найти области применения невозможных фигур.
Задачи проекта:
1.Изучить литературу по теме «Невозможные фигуры».
2.Составить классификацию невозможных фигур.
3.Рассмотреть способы построения невозможных фигур.
4.Создать невозможную фигуру.
Тема моей работы актуальна ведь понимание парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Многие работы с нереальными объектами можно отнести к «интеллектуальным математическим играм». Моделировать подобный мир можно только с помощью математических формул, человек представить его просто не в состоянии. И для развития пространственного воображения оказываются полезными невозможные фигуры. Человек неустанно мысленно создает вокруг себя то, что для него будет просто и понятно. Он даже не может себе представить, что некоторые объекты, окружающие его, могут быть «невозможными». На самом деле мир един, но рассматривать его можно с разных сторон.
Невозможные фигуры
Немного из истории
Невозможные фигуры достаточно часто встречаются на древних гравюрах, картинах и иконах - в одних случаях мы имеем с явными ошибками передачи перспективы, в других - с умышленными искажениями, обусловленными художественным замыслом.
Мы привыкли верить фотографиям (и несколько в меньшей степени - чертежам и рисункам), наивно полагая, что они всегда соответствуют какой-то действительности (реальной или вымышленной). Примером первой является параллелепипед, второй - эльф или другой сказочный зверь. Отсутствие эльфов в наблюдаемой нами области пространства/времени еще не означает, что они не могут существовать. Еще как могут (в чем легко убедиться с помощью гипса, пластилина или папье-маше). А вот как нарисовать то, чего вообще не может быть?! Что вообще нельзя сконструировать?!
Существует огромный класс так называемых "невозможных фигур", ошибочно или умышленно нарисованных с ошибками передачи перспективы, в результате чего возникают забавные визуальные эффекты, помогающие психологам разобраться с принципами работы (под)сознания.
В средневековой японской и персидской живописи невозможные объекты являются неотъемлемой частью восточного художественного стиля, дающего лишь общий набросок картины, детали которой "приходится" додумывать зрителю самостоятельно, в соответствии со своими предпочтениями. Вот перед нами школа. Наше внимание привлекает архитектурное сооружение на заднем плане, геометрическая противоречивость которого очевидна. Его можно интерпретировать и как внутреннюю стену комнаты, и как наружную стену здания, но обе эти интерпретации неправильны, поскольку мы имеем дело с плоскостью, одновременно являющуюся и внешней, и наружной стенкой, то есть на картине изображен типичный невозможный объект.

Картины с искаженной перспективой встречаются уже в начале первого тысячелетия. На миниатюре из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене, нарисована Мадонна с младенцем. На картине изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект нереальности.

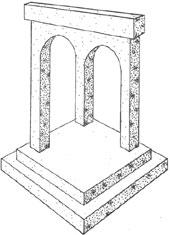
В статье "Наведение порядка в невозможном" (impossible.info/russian/articles/kulpa/putting-order.html) дается следующее определение невозможных фигур: "Невозможная фигура - это плоский рисунок, который создает впечатление трехмерного объекта таким образом, что объект, предложенный нашим пространственным восприятием, не может существовать, так что попытка создать его ведет к (геометрическим) противоречиям, ясно видимыми наблюдателем". Примерно то же самое пишут и Пенроузы в своей памятной статье: "Каждая отдельная часть фигуры выглядит нормальным трехмерным объектом, но вследствие неправильного соединения частей фигуры восприятие фигуры полностью приводит к иллюзорному эффекту невозможности", но никто из них не отвечает на вопрос: почему все это происходит?
Между тем все просто. Наше восприятие устроено так, что при обработке двухмерной фигуры, имеющей признаки перспективы (т.е. объемного пространства), мозг воспринимает ее как трехмерную, выбирая наиболее простой способ преобразования 2D в 3D, руководствуясь жизненным опытом, а как было показано выше, реальные прототипы "невозможных" фигур представляют собой довольно навороченные конструкции, с которыми наше подсознание незнакомо, но даже после знакомства с ними, мозг по-прежнему продолжает выбирать простейший (с его точки зрения) вариант преобразования и только после длительных тренировок подсознание наконец "въезжает в ситуацию" и кажущаяся ненормальность "невозможных фигур" исчезает.
Начнем с легкого. Рассмотрим картину (да, да, именно картину, а не фотореалистичный рисунок, сгенерированный компьютером), нарисованную фламандским художником по имени Жос де Мей/Jos de Mey . Вопрос - какой физической действительности она могла бы соответствовать?
На первый взгляд архитектурное сооружение кажется невозможным, но после секундной заминки сознание находит спасательный вариант: кирпичная кладка находится в плоскости, перпендикулярной наблюдателю и опирается на три колонны, вершины которых кажутся расположенными на равном расстоянии от кладки, но на самом деле пустое пространство просто "скрадывается" за счет "удачно" выбранной проекции. После того, как сознание "расшифровало" картину, она (и все подобные ей изображения) воспринимается совершенно нормально и геометрические противоречия исчезают также незаметно, как и появляются.

Невозможная картина Жоса де Мея
Рассмотрим знаменитую картину Мориса Эшера/Maurits Escher "Водопад"/"Waterfall" и ее упрощенную компьютерную модель, выполненную в фотореалистичном стиле . На первый взгляд никаких парадоксов нет, перед нами обыкновенная картина, изображающая... чертеж вечного двигателя!!! Но ведь, как известно из школьного курса физики, вечный двигатель невозможен! Как же Эшеру удалось с такими подробностями изобразить то, чего в природе вообще не может быть?!

Вечный двигатель на гравюре "Водопад" Эшера.

Компьютерная модель вечного двигателя Эшера.
При попытке соорудить двигатель согласно чертежу (или при внимательном анализе последнего) "обман" всплывает сразу - в трехмерном пространстве такие конструкции геометрически противоречивы и могут существовать только на бумаге, то есть на плоскости, а иллюзия "объема" создается лишь за счет признаков перспективы (в данном случае - умышленно искаженных) и на уроке черчения за такой шедевр нам запросто влепят два балла, указав на ошибки выполнения проекции.
Виды невозможных фигур.
"Невозможные фигуры" делятся на 4 группы. Итак, первая:
Удивительный треугольник – трибар.
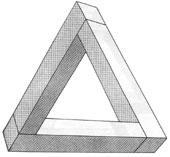
Эта – фигура – возможно первый опубликованный в печати невозможный объект. Она появилась в 1958 году. Её авторы, отец и сын Лайонелл и Роджер Пенроузы, генетик и математик соответственно, определили этот объект как "трехмерную прямоугольную структуру". Она также получила название "трибар". С первого взгляда трибар кажется просто изображением равностороннего треугольника. Но стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В тоже время левая и правая грани внизу тоже кажутся перпендикулярными. Если смотреть на каждую деталь отдельно, то она кажется реальной, но, в общем, эта фигура существовать не может. Она не деформирована, но при черчении были неправильно соединены правильные элементы.
Вот еще несколько примеров невозможных фигур на основе трибара.
|  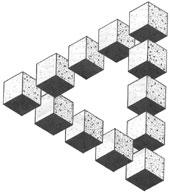
Тройной деформированный трибар Треугольник из 12 кубов
|
|
|  
Крылатый трибар Тройное домино
Знакомство с невозможными фигурами (особенно в исполнении Эшера), конечно, ошеломляет, но тот факт, что любую из невозможных фигур возможно сконструировать в реальном трехмерном мире, приводит в недоумение. Как известно, всякое двухмерное изображение представляет собой проекцию трехмерной фигуры на плоскость (лист бумаги). Способов проекции существует достаточно много, но в рамках каждого из них отображение выполняется однозначно, то есть существует строгое соответствие между трехмерной фигурой и ее двухмерным изображением. Однако аксонометрические, изометрические и другие популярные способы проекции являются однонаправленными преобразованиями, осуществляемыми с потерей информации и потому обратное преобразование может быть выполнено бесконечным множеством способов, то есть двухмерному изображению соответствует бесконечное множество трехмерных фигур и любой математик без труда докажет, что такое преобразование возможно для любого двухмерного изображения. То есть, на самом деле никаких невозможных фигур нет! Вернемся к Треугольнику Пенроуза и попробуем соорудить трехмерную фигуру, проекция которой на двухмерную плоскость выглядела бы обозначенным образом. Естественно, напрямую такую задачу решить не удастся, но если хорошо подумать и выбрать правильный ракурс, то... один из возможных вариантов показан на рисунке. 
Возможный невозможный Треугольник Пенроуза. А вот другое отображение от Матье Хемакерза. Возможных вариантов обратного отображения много. Очень много. Бесконечно много! 
Все тот же Треугольник Пенроуза в различных ракурсах. Кстати говоря, Треугольник Пенроуза увековечен в виде статуи в Перте (Австралия). Созданный усилиями художника Брайна МакКея/Brian McKay и архитектора Ахмада Абаса/Ahmad Abas, он был воздвигнут в парке Клайзебрук/Claisebrook в 1999 году и теперь все проезжающие мимо могут видеть следующую "невозможную" фигуру. 
Треугольник Пероуза в Австралии Но стоит изменить угол зрения, как треугольник из "невозможного" превращается в реальное и эстетически непривлекательное сооружение, не имеющее к треугольникам никакого отношения .  
Так выглядит Треугольник Пенроуза на самом деле.
|
|
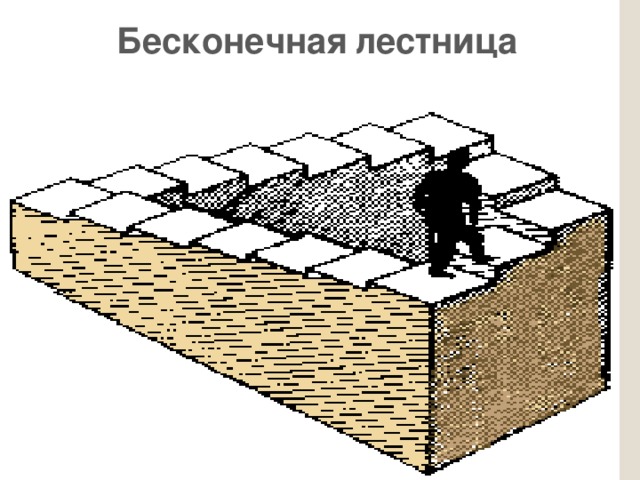
Бесконечная лестница
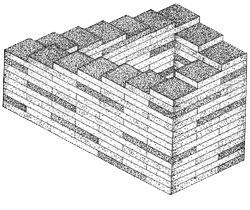

Эту фигуру чаще всего называют "Бесконечной лестницей", "Вечной лестницей" или "Лестницей Пенроуза" – по имени ее создателя. Ее также называют "непрерывно восходящей и нисходящей тропой".
Впервые эта фигура была опубликована в 1958 году. Перед нами предстает лестница, ведущая, казалось бы, вверх или вниз, но при этом, человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути.
"Бесконечной лестницей" с успехом воспользовался художник Мауриц К. Эшер, на этот раз в своей литографии "Восхождение и нисхождение", созданной в 1960 году.
Лестница с четырьмя или семью ступеньками. На создание этой фигуры с большим количеством ступенек автора могла вдохновить куча обыкновенных железнодорожных шпал. Собравшись взобраться на эту лестницу, вы будете стоять перед выбором: подняться ли по четырем или по семи ступенькам.
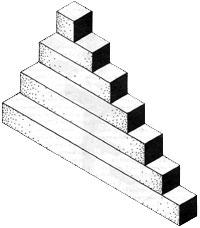
Создатели этой лестницы воспользовались параллельными линиями при разработке конечных деталей блоков, находящихся на одинаковом расстоянии; кажется, что некоторые блоки перекручиваются, чтобы соответствовать иллюзии.
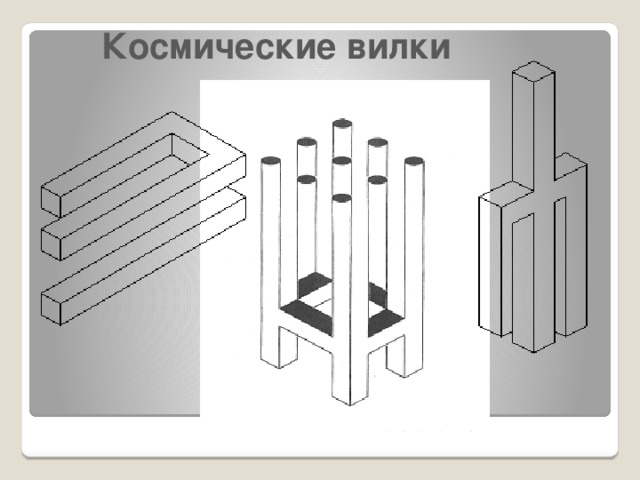
Космическая вилка.
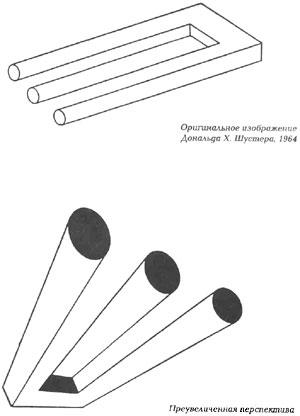
Следующая группа фигур под общим названием "Космическая вилка". С этой фигурой мы входим в самую сердцевину и суть невозможного. Может быть, это самый многочисленный класс невозможных объектов.
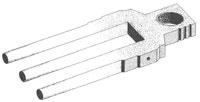
Этот пресловутый невозможный объект с тремя (или с двумя?) зубцами стал популярен у инженеров и любителей головоломок в 1964 году. Первая публикация, посвященная необычной фигуре, появилась в декабре 1964 года. Автор назвал ее "Скобой, состоящей из трех элементов".
С практической точки зрения этот странный трезубец или механизм в виде скобы, абсолютно неприменим. Некоторые называют его просто "досадной ошибкой". Один из представителей аэрокосмической промышленности предложил использовать его свойства при конструировании межпространственного космического камертона.
| 
| 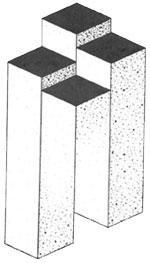
Башня с четырьмя колоннами-близнецами.
|
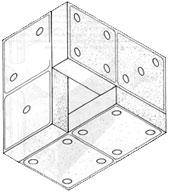
Невозможные ящики
Еще один невозможный объект появился в 1966 году в Чикаго в результате оригинальных экспериментов фотографа доктора Чарльза Ф. Кокрана. Многие любители невозможных фигур проводили эксперименты с "Сумасшедшим ящиком". Первоначально автор назвал ее "Свободным ящиком" и заявил, что она была "сконструирована для пересылки невозможных объектов в большом количестве".
"Сумасшедший ящик" – это вывернутый наизнанку каркас куба. Непосредственным предшественником "Сумасшедшего ящика" была "Невозможная коробка" (автор Эшер), а ее предшественником в свою очередь стал куб Неккера.

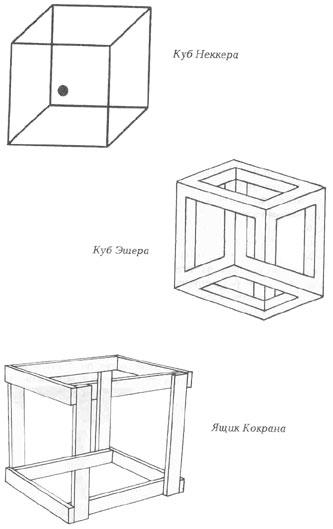
Он не является невозможным объектом, однако представляет собой фигуру, в которой параметр глубины может восприниматься неоднозначно.
Когда мы вглядываемся в куб Неккера, то замечаем, что грань с точкой находится то на переднем, то на заднем плане, она перепрыгивает из одного положения в другое.
Оскар Рутерсвард – отец невозможной фигуры.
«Отцом» невозможных фигур считается шведский художник Оскар Рутерсвард. Шведский художник Оскар Рутерсвард, специалист по созданию изображений невозможных фигур утверждал, что плохо разбирается в математике, но, тем не менее, возвел свое искусство в ранг науки, создав целую теорию создания невозможных фигур по определенному ряду шаблонов.
Пара невозможных фигур от Оскара Реутерсварда.
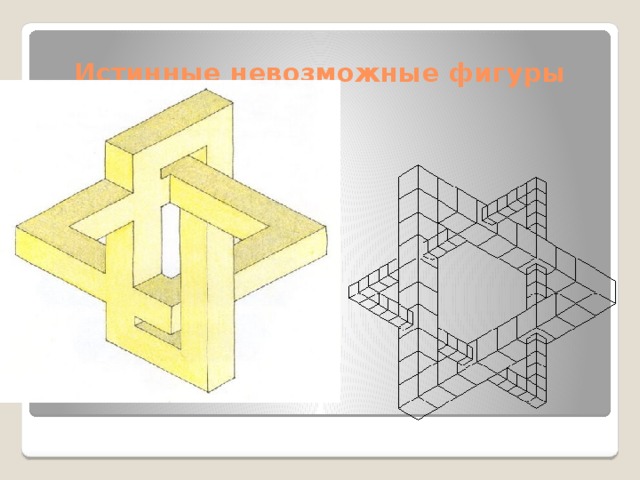
Он разделил фигуры на две основные группы. Один из них он назвал «истинные невозможные фигуры». Это двухмерные изображения трёхмерных тел, которые на бумаге можно раскрасить и нанести на них тени, но у них нет монолитной и стабильной глубины.
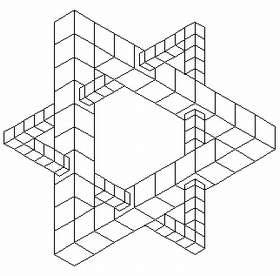
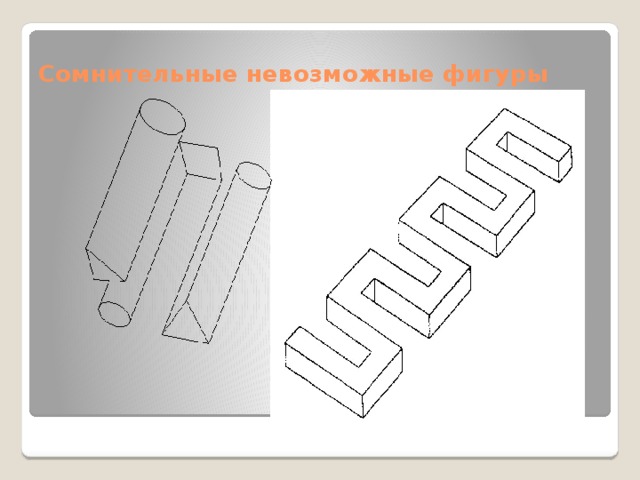
Другой вид – сомнительные невозможные фигуры. Эти фигуры не представляют собой единых цельных тел. Они являются соединением двух или большего числа фигур. Их нельзя ни раскрасить, ни нанести на них свет и тени.
Истинная невозможная фигура состоит из фиксированного количества возможных элементов, а сомнительная «теряет» некоторое количество элементов, если за ними проследить глазами.
Один вариант этих невозможных фигур очень легко выполнить, и многие из тех, кто машинально чертит геометрические фигуры, когда разговаривает по телефону, это уже не раз делали. Нужно провести пять, шесть или семь параллельных линий, закончить эти линии в разных концах по-разному – и невозможная фигура готова. Если, например, провести пять параллельных линий, то их можно закончить как две балки с одной стороны и три с другой.
На рисунке мы видим три варианта сомнительных невозможных фигур. Слева трех-семибалочник, построенный из семи линий, в котором три балки превращаются в семь. Фигура в середине, построенная из трех линий, в которой одна балка превращается в два круглых бруса. Фигура справа, построенная из четырех линий, в которой два круглых бруса превращаются в две балки
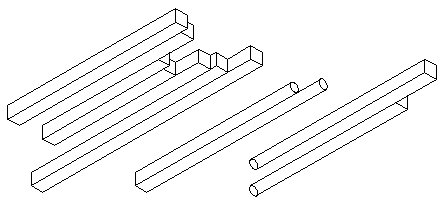
За свою жизнь Рутерсвард изобразил около 2500 фигур. Книги Рутерсварда опубликованы на многих языках, в том числе на русском.
Невозможные фигуры - возможны!
Многие полагают, что невозможные фигуры действительно невозможны, и их нельзя создать в реальном мире. Но надо помнить, что любой рисунок на листе бумаги - это проекция трехмерной фигуры. Следовательно, любая фигура, нарисованная на листе бумаги, должна существовать в трехмерном пространстве. Невозможные объекты на картинах представляют собой проекции трехмерных объектов, а значит, объекты можно реализовать в виде скульптурных композиций. Существует множество способов их создания. Один из них - использование кривых линий в качестве сторон невозможного треугольника. Созданная скульптура выглядит невозможной только из единственной точки. Из этой точки кривые стороны выглядят прямыми, и поставленная цель будет достигнута - создан реальный "невозможный " объект.
Русский художник Анатолий Коненко, наш современник, разделил невозможные фигуры на 2 класса: одни можно смоделировать в реальности, а другие – нельзя. Модели невозможных фигур называются моделями Амес.
Я изготовил свою невозможную фигуру. Я взял сорок два кубика и склеил их, получился куб, в котором часть ребра отсутствует. Отмечу, что для создания полной иллюзии необходим правильный угол зрения и верное освещение.
Я создаю свои невозможные фигуры, пользуясь советом О.Рутерсварда. Я начертил на бумаге семь параллельных отрезков. Соединила их снизу ломаной линией, а сверху придала им форму параллелепипедов. Посмотрите на нее сначала сверху потом снизу. Таких фигур можно придумать бесконечно много.
Применение невозможных фигур
Невозможные фигуры находят иногда неожиданное применение. Оскар Рутерсвард рассказывает в книге "Omojliga figurer" об использовании рисунков имп-арта для психотерапии. Он пишет, что картины своими парадоксами вызывают удивление, заостряют внимание и желание расшифровать. Психолог Роджер Шепард использовал идею трезубца для своей картины невозможного слона.
В Швеции их применяют в зубоврачебной практике: рассматривая картины в приемной, пациенты отвлекаются от неприятных мыслей перед кабинетом стоматолога.
Невозможные фигуры вдохновили художников на создание целого нового направления в живописи, названного импоссибилизмом. К импоссибилистам относят голландского художника Эшера . Его перу принадлежат известные литографии «Водопад», «Восхождение и нисхождение» и «Бельведер». Художник использовал эффект "бесконечной лестницы", открытый Рутесвардом.
За рубежом, на улицах городов, мы можем увидеть архитектурные воплощения невозможных фигур.
Наиболее известное использование невозможных фигур в массовой культуре — логотипавтоконцерна «Рено»
Математики утверждают, что и дворцы, в которых можно спуститься вниз по лестнице, ведущей вверх, могут существовать. Для этого нужно лишь построить такое сооружение не в трехмерном, а, скажем, в четырехмерном пространстве. А уж в виртуальном мире, который открывает нам современная компьютерная техника, и не такое можно натворить. Вот так в наши дни осуществляются задумки человека, который еще на заре века поверил в существование невозможных миров.
Заключение.
Невозможные фигуры заставляют наш разум сначала увидеть то, чего быть не должно, затем искать ответ - что же сделано не так, в чем скрыта изюминка парадокса. А ответ найти порой не так - то просто - он скрыт в оптическом, психологическом, логическом восприятии рисунков.
Развитие науки, необходимость мыслить по-новому, поиски прекрасного - все эти требования современной жизни заставляют искать новые методы, которые способны изменить пространственное мышление, воображение.
Изучив литературу по теме, я смог ответить на вопрос «Существуют ли в реальном мире невозможные фигуры?» Я понял, что невозможное возможно и нереальные фигуры можно сделать своими руками. Я создал модель Амес «Невозможного куба». Рассмотрев способы построения невозможных фигур, я смог нарисовать свои невозможные фигуры. Мне удалось показать, что
Вывод: Все невозможные фигуры могут существовать в реальном мире.
Найдется ещё много областей, в которых будут использоваться невозможные фигуры.
Таким образом, можно сказать, что мир невозможных фигур чрезвычайно интересен и многообразен. Изучение невозможных фигур имеет довольно важное значение с точки зрения геометрии. Работа может быть использована на занятиях по математике для развития пространственного мышления учащихся. Для творческих людей, склонных к изобретательству, невозможные фигуры являются своеобразным рычагом для создания чего-то нового, необычного.
Список литературы
Левитин Карл Геометрическая рапсодия. - М.: Знание, 1984, -176 с.
Пенроуз Л., Пенроуз Р. Невозможные объекты, Квант, № 5,1971, с.26
Реутерсвард О. Невозможные фигуры. – М.: Стройиздат,1990, 206 с.
Ткачева М.В. Вращающиеся кубики. – М.: Дрофа, 2002. – 168 с.
Интернет ресурсы:
http://wikipedia.tomsk.ru
http://www.konenko.net/imp.htm
http://www.im-possible.info/russian/articles/reut_imp/
9