ПрактическАЯ РАБОТА№ 1
Тема: Предел функции в точке. Раскрытие неопределенностей
Цели:
- ознакомиться с понятием предела числовой последовательности;
- ознакомиться с понятием предела функции;
- научиться раскрывать неопределенности вида.
Оснащение занятия: конспект лекций.
Критерии оценок
оценка «5» ставится за верное выполнение всех заданий работы
оценка «4» ставится за верное выполнение любых девяти заданий работы
оценка «3» ставится за выполнение любых семи заданий работы
Порядок выполнения работы
Задание 1.
1. Ознакомиться с лекциями 1,2,3.
2. Выписать в тетрадь теоремы о пределах
3. Записать в тетрадь решение примеров 1 – 6.
Лекция 1.
Тема «Числовые последовательности. Их роль в вычислительных процессах. Предел числовой последовательности»
Бесконечной числовой последовательностью называется числовая функция, определенная на множестве N натуральных чисел.
Последовательность (xn) называется возрастающей (убывающей), если каждый её член, начиная со второго, больше (меньше) предыдущего, т. е. если для любого n выполняется неравенство xn+1 >xn (xn+1<xn).
Последовательность (xn) называется невозрастающей (неубывающей), если каждый её член, начиная со второго, не больше (не меньше) предыдущего, т. е. если для любого n выполняется неравенство xn+1 xn (xn+1 xn).
Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными.
Последовательность (xn) называется ограниченной сверху (ограниченной снизу), если можно указать такое число М (число m), что для всех членов этой последовательности выполняется неравенство xn
(xn . Числа Mи mназываются соответственно верхней и нижней границами последовательности (xn). Тот факт, что последовательность ограничена сверху числомM (снизу числомm), геометрически означает, что ни одна точкаxn не лежит правее точкиM (левее точкиm).
Последовательность (xn) называется ограниченной, если существуют два числаm и M такие, что для всех nвыполняется неравенство m . Тот факт, что последовательность ограничена числамиm и, геометрически означает, что все её члены помещаются в промежутке [m;M].
Последовательность (xn) называется постоянной, если все её члены совпадают.
Обычно последовательность задаётся формулой, выражающей общий член последовательности через n. Иногда указывается правило, с помощью которого можно вычислить n-й член последовательности по её известным предыдущим членам. Такой способ задания последовательности называется индуктивным(или реккурентным).
Пример. Вычислить пять первых членов последовательности xn =
Подставив вместо n последовательно 1, 2, 3, 4, 5, получим
ПрактическАЯ РАБОТА№ 1
Тема: Предел функции в точке. Раскрытие неопределенностей
Цели:
- ознакомиться с понятием предела числовой последовательности;
- ознакомиться с понятием предела функции;
- научиться раскрывать неопределенности вида.
Оснащение занятия: конспект лекций.
Критерии оценок
оценка «5» ставится за верное выполнение всех заданий работы
оценка «4» ставится за верное выполнение любых девяти заданий работы
оценка «3» ставится за выполнение любых семи заданий работы
Порядок выполнения работы
Задание 1.
1. Ознакомиться с лекциями 1,2,3.
2. Выписать в тетрадь теоремы о пределах
3. Записать в тетрадь решение примеров 1 – 6.
Лекция 1.
Тема «Числовые последовательности. Их роль в вычислительных процессах. Предел числовой последовательности»
Бесконечной числовой последовательностью называется числовая функция, определенная на множестве N натуральных чисел.
Последовательность (xn) называется возрастающей (убывающей), если каждый её член, начиная со второго, больше (меньше) предыдущего, т. е. если для любого n выполняется неравенство xn+1 >xn (xn+1<xn).
Последовательность (xn) называется невозрастающей (неубывающей), если каждый её член, начиная со второго, не больше (не меньше) предыдущего, т. е. если для любого n выполняется неравенство xn+1 xn (xn+1 xn).
Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными.
Последовательность (xn) называется ограниченной сверху (ограниченной снизу), если можно указать такое число М (число m), что для всех членов этой последовательности выполняется неравенство xn
(xn . Числа Mи mназываются соответственно верхней и нижней границами последовательности (xn). Тот факт, что последовательность ограничена сверху числомM (снизу числомm), геометрически означает, что ни одна точкаxn не лежит правее точкиM (левее точкиm).
Последовательность (xn) называется ограниченной, если существуют два числаm и M такие, что для всех nвыполняется неравенство m . Тот факт, что последовательность ограничена числамиm и, геометрически означает, что все её члены помещаются в промежутке [m;M].
Последовательность (xn) называется постоянной, если все её члены совпадают.
Обычно последовательность задаётся формулой, выражающей общий член последовательности через n. Иногда указывается правило, с помощью которого можно вычислить n-й член последовательности по её известным предыдущим членам. Такой способ задания последовательности называется индуктивным(или реккурентным).
Пример. Вычислить пять первых членов последовательности xn =
Подставив вместо n последовательно 1, 2, 3, 4, 5, получим
ПрактическАЯ РАБОТА№ 1
Тема: Предел функции в точке. Раскрытие неопределенностей
Цели:
- ознакомиться с понятием предела числовой последовательности;
- ознакомиться с понятием предела функции;
- научиться раскрывать неопределенности вида.
Оснащение занятия: конспект лекций.
Критерии оценок
оценка «5» ставится за верное выполнение всех заданий работы
оценка «4» ставится за верное выполнение любых девяти заданий работы
оценка «3» ставится за выполнение любых семи заданий работы
Порядок выполнения работы
Задание 1.
1. Ознакомиться с лекциями 1,2,3.
2. Выписать в тетрадь теоремы о пределах
3. Записать в тетрадь решение примеров 1 – 6.
Лекция 1.
Тема «Числовые последовательности. Их роль в вычислительных процессах. Предел числовой последовательности»
Бесконечной числовой последовательностью называется числовая функция, определенная на множестве N натуральных чисел.
Последовательность (xn) называется возрастающей (убывающей), если каждый её член, начиная со второго, больше (меньше) предыдущего, т. е. если для любого n выполняется неравенство xn+1 >xn (xn+1<xn).
Последовательность (xn) называется невозрастающей (неубывающей), если каждый её член, начиная со второго, не больше (не меньше) предыдущего, т. е. если для любого n выполняется неравенство xn+1 xn (xn+1 xn).
Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными.
Последовательность (xn) называется ограниченной сверху (ограниченной снизу), если можно указать такое число М (число m), что для всех членов этой последовательности выполняется неравенство xn
(xn . Числа Mи mназываются соответственно верхней и нижней границами последовательности (xn). Тот факт, что последовательность ограничена сверху числомM (снизу числомm), геометрически означает, что ни одна точкаxn не лежит правее точкиM (левее точкиm).
Последовательность (xn) называется ограниченной, если существуют два числаm и M такие, что для всех nвыполняется неравенство m . Тот факт, что последовательность ограничена числамиm и, геометрически означает, что все её члены помещаются в промежутке [m;M].
Последовательность (xn) называется постоянной, если все её члены совпадают.
Обычно последовательность задаётся формулой, выражающей общий член последовательности через n. Иногда указывается правило, с помощью которого можно вычислить n-й член последовательности по её известным предыдущим членам. Такой способ задания последовательности называется индуктивным(или реккурентным).
Пример. Вычислить пять первых членов последовательности xn =
Подставив вместо n последовательно 1, 2, 3, 4, 5, получим
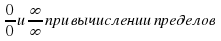 .
. 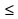 xn (xn+1
xn (xn+1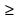 xn).
xn).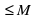
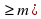 . Числа Mи mназываются соответственно верхней и нижней границами последовательности (xn). Тот факт, что последовательность ограничена сверху числомM (снизу числомm) , геометрически означает, что ни одна точкаxn не лежит правее точкиM (левее точкиm).
. Числа Mи mназываются соответственно верхней и нижней границами последовательности (xn). Тот факт, что последовательность ограничена сверху числомM (снизу числомm) , геометрически означает, что ни одна точкаxn не лежит правее точкиM (левее точкиm).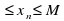 . Тот факт, что последовательность ограничена числамиm и
. Тот факт, что последовательность ограничена числамиm и 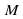 , геометрически означает, что все её члены помещаются в промежутке [m;M].
, геометрически означает, что все её члены помещаются в промежутке [m;M].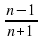
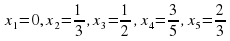
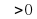 все члены последовательностиxn, кроме, быть может, конечного их числа, лежат в
все члены последовательностиxn, кроме, быть может, конечного их числа, лежат в  - окрестности (а-
- окрестности (а-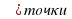 а, т. е. найдется такое натуральное число N, что при nN выполняется неравенство
а, т. е. найдется такое натуральное число N, что при nN выполняется неравенство 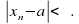
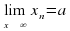 В этом случае говорят, что последовательность сходится к числу а.
В этом случае говорят, что последовательность сходится к числу а.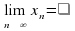 а, необходимо и достаточно, чтобы xn = a +
а, необходимо и достаточно, чтобы xn = a +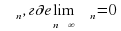
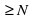 выполняется неравенство
выполняется неравенство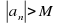 . В этом случае пишут
. В этом случае пишут 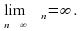
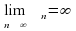 и все числа
и все числа 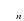 , начиная с некоторого номера N, положительны, то последовательность (an) стремится к +
, начиная с некоторого номера N, положительны, то последовательность (an) стремится к +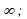 если все числа
если все числа 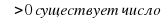
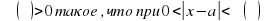 выполняется неравенство:
выполняется неравенство: 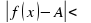 . Это записывается так:
. Это записывается так: 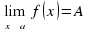
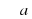 , если:
, если: 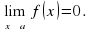
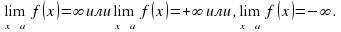
 F(x) – есть функция бесконечно малая.
F(x) – есть функция бесконечно малая.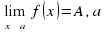 функция g(x) – бесконечно большая, то
функция g(x) – бесконечно большая, то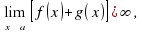 а
а 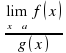 = 0
= 0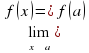
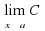 = С
= С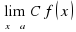 = С
= С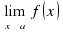
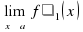 и
и 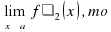
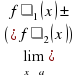 = (предел суммы
= (предел суммы















