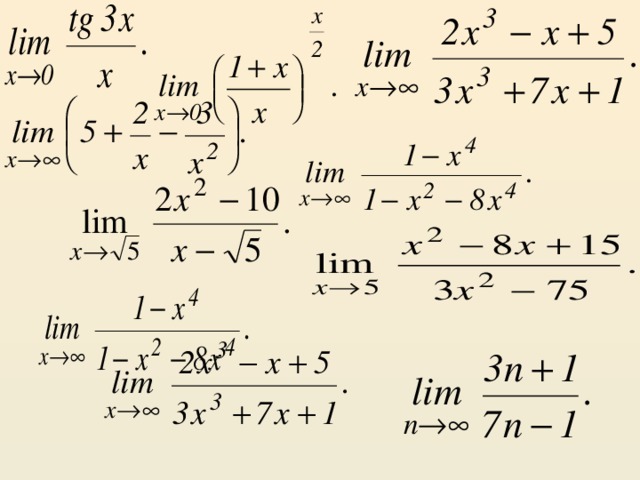Урок комбинированного типа на тему: "Пределы функции. Замечательные пределы"
Цели урока:
- Учебная: закрепить понятие предел функции в точке, на бесконечности, ввести понятие замечательный предел, приобрести навыки вычисления пределов функций.
- Воспитательная: воспитывать ответственное отношение к учебному труду, волю; формировать культуру речи в использовании необходимой терминологии; воспитывать здоровую конкуренцию, взаимовыручку.
- Развивающая: развить умение работать в команде, помочь товарищу развить умение вычислять пределы функции, применять терминологию.
- Деятельностная: применять теорию пределов при решении задач, умение вычислять пределы функции, уметь правильно оценить себя и товарищей.
ХОД ЗАНЯТИЯ
- Организационный момент
Приветствие
Распределение по рабочим местам
Проверка присутствующих
Сообщение темы, целей, задач и плана урока
Мотивация на положительный настрой, организация рабочей обстановки
- Разминка, представление команд.
Представление команд: капитан, название, эмблема, девиз.
Представление жюри
Тест настроение
Математическая разминка
- Актуализация знаний
Теоретические шифровальщики
Математические регулировщики
Математическое лото для практиков
Чтение графика (резерв)
Релаксация. Предварительное подведение итогов
- Объяснение нового материала
История развития математического анализа, теории пределов.
Первый замечательный предел и его следствия, решение примеров.
Второй замечательный предел и его следствия, решение примеров.
Решение задач преподавателем у доски
- Закрепление изученного материала
Решение задач членами команд
Решение индивидуальных заданий
Подведение итогов соревнований жюри
- Домашнее задание
Представление д/з капитанами команд, обмен подарками- д/з
- Подведение итогов урока
Тест настроение
Итоги соревнования, оценки, анализ урока
Уборка учебных мест
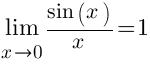
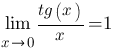
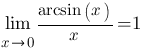
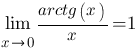
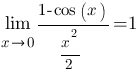
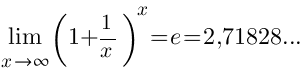
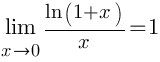
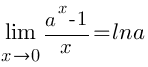
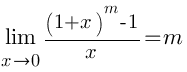
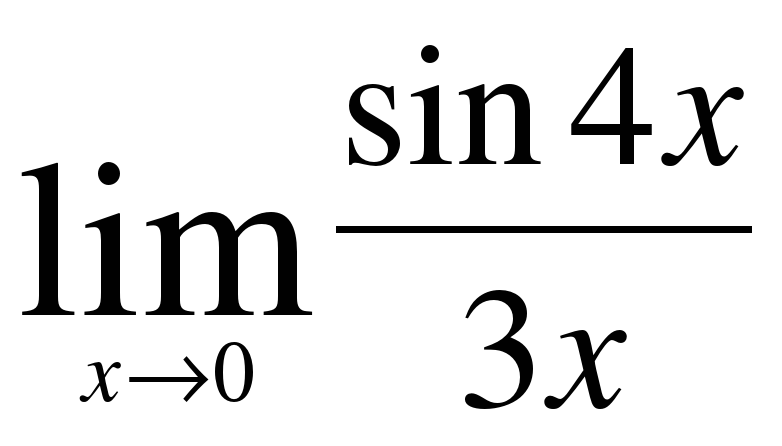
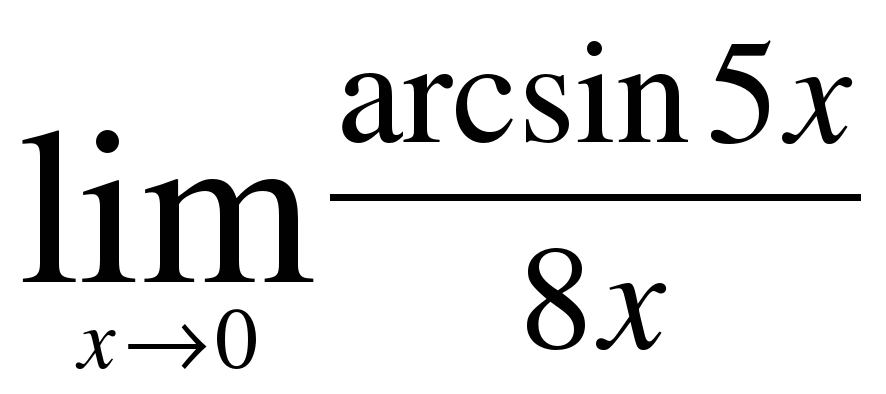
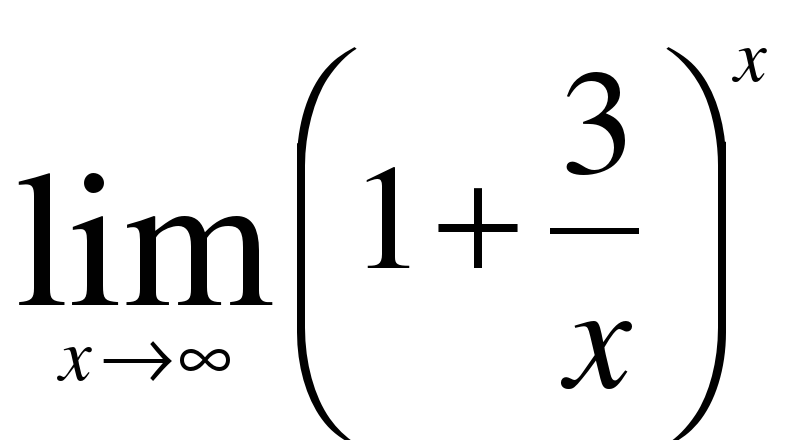
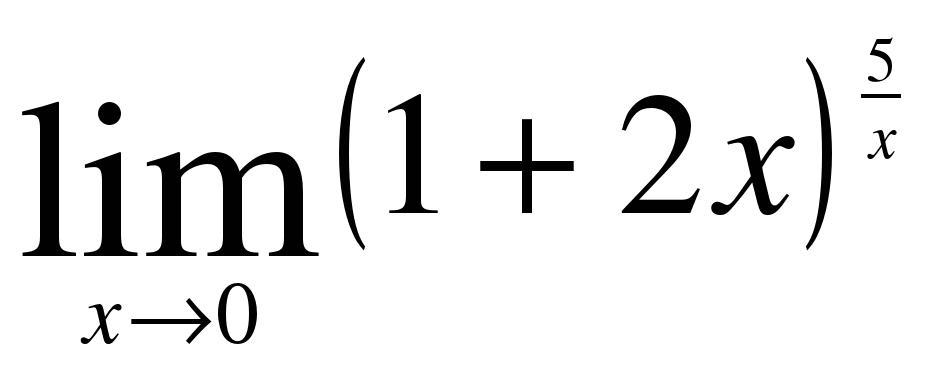
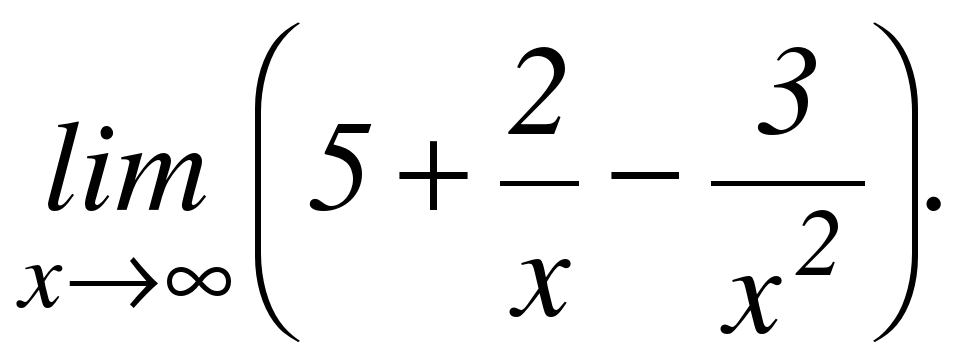
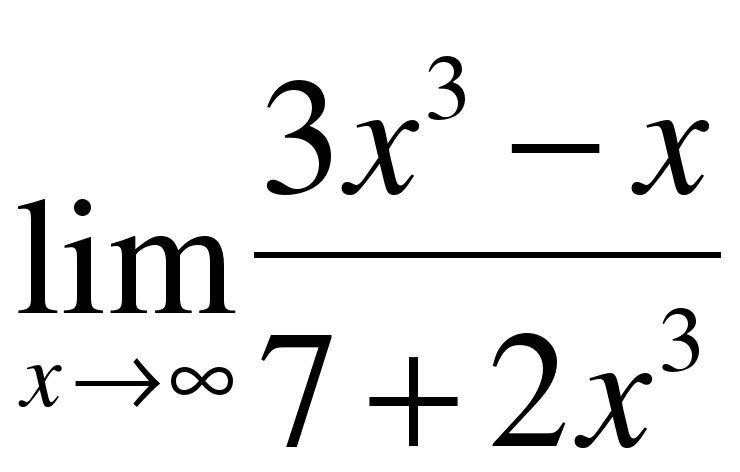
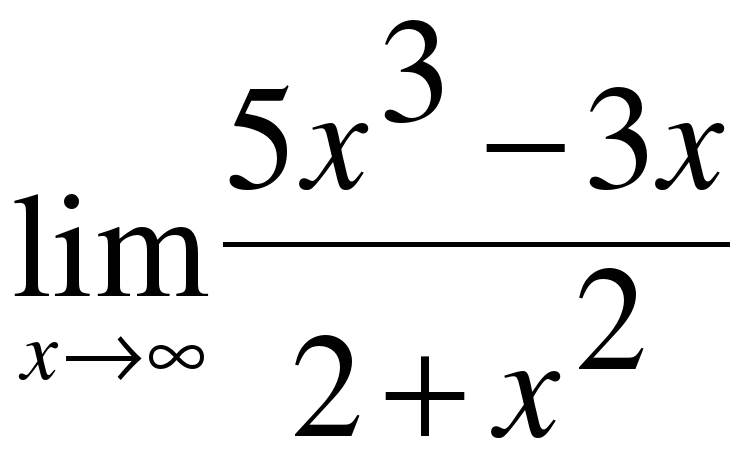
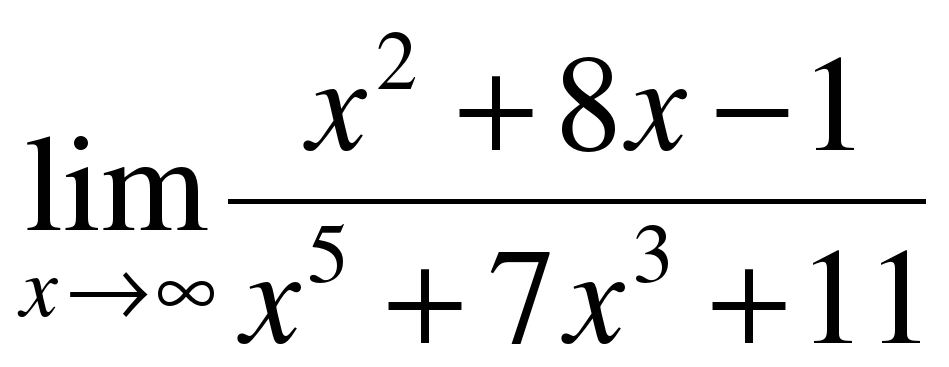
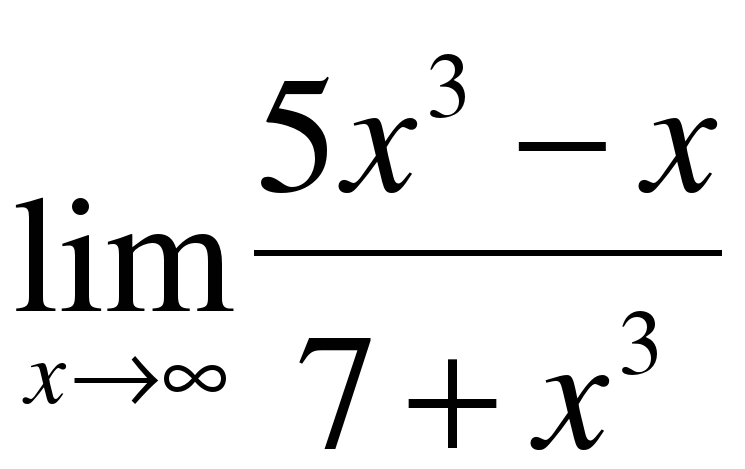
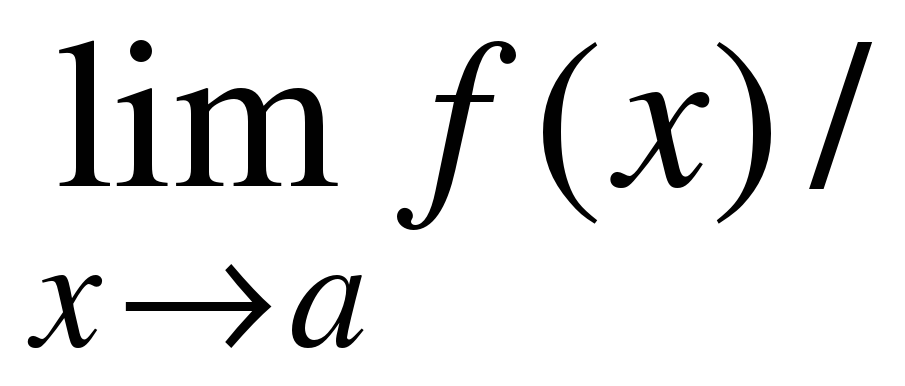
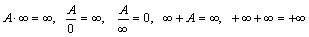
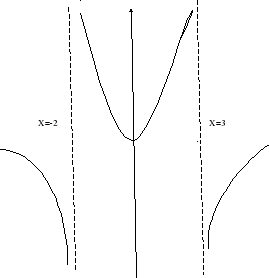

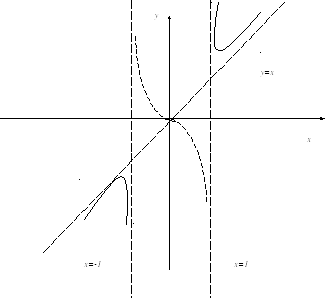





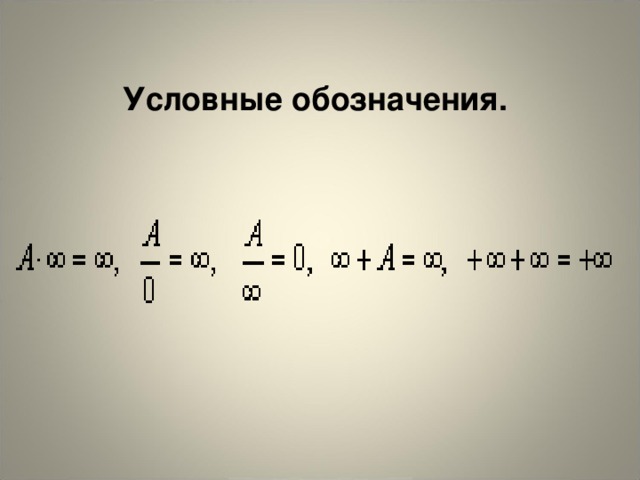
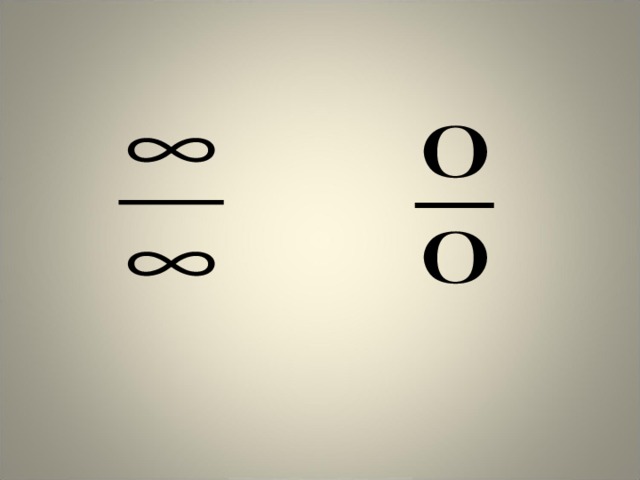




















 0 0 δ ≠ ε b точке =_____ ( предел в _______)" width="640"
0 0 δ ≠ ε b точке =_____ ( предел в _______)" width="640"
 __, выполняется неравенство |f(x) - b| → b ε M b бесконечности (предел на ______________)" width="640"
__, выполняется неравенство |f(x) - b| → b ε M b бесконечности (предел на ______________)" width="640"