Митрофанова Снежана Викторовна, МБОУ «Верховская школа» Вологодская область
Тема: Практикум по решению задач по теории вероятности.
СЛАЙД 1
Как решать задачи на вероятность?
Вероятность. Что это?
СЛАЙД 2
Теория вероятностей, как следует из названия, имеет дело с вероятностями. Нас окружают множество вещей и явлений, о которых, как бы ни была развита наука, нельзя сделать точных прогнозов. Мы не знаем, какую карту вытянем из колоды наугад или сколько дней в мае будет идти дождь, но, имея некоторую дополнительную информацию, можем строить прогнозы и вычислять вероятности этих случайных событий.
Таким образом, мы сталкиваемся с основным понятием случайного события -это явления, поведение которого невозможно предсказать, или это опыта, результат которого заранее невозможно вычислить и т.п. Именно вероятности событий вычисляются в типовых задачах ЕГЭ.
СЛАЙД 2 (ЕЩЁ РАЗ)
Вероятность - это некоторая, строго говоря, функция, принимающая значения от 0 до 1 и характеризующая данное случайное событие.
Затем используем примерную схему, по которой следует решать стандартные учебные задачи на вычисление вероятности случайного события,
СЛАЙД 3
а затем ниже на примерах я проиллюстрирую ее применение.
Внимательно прочитать задачу и понять, что именно происходит
Найти основной вопрос задачи(найти что является исход задачи , найти благоприятные исходы. )
Выбрать формулу (или несколько) для решения.
СЛАЙД 4
ПОЧЕМУ МЫ ВНИМАТЕЛЬНО ЧИТАЕМ ЗАДАЧИ?
Из 20 билетов, предлагаемых на экзамене, школьник может ответить только на 17. Какова вероятность того, что школьник сможет ответить на выбранный наугад билет?
Из 20 билетов, предлагаемых на экзамене, школьник может ответить только на 17. Какова вероятность того, что школьник не сможет ответить на выбранный наугад билет?
СЛАЙД 5,6,7



СЛАЙД 8,9



СЛАЙД 10
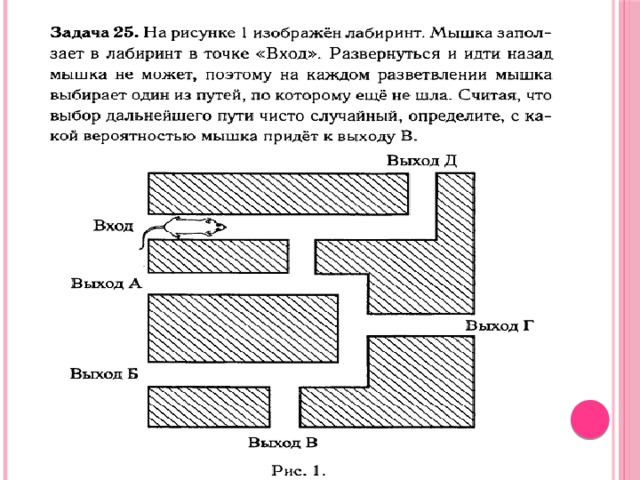
Задачи, решаемые с помощью построения дерева вероятностей.
Задача 1.
Павел Иванович совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно.Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку G .
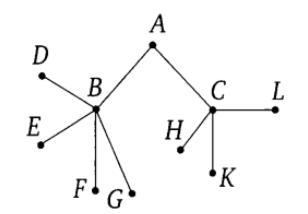
СЛАЙД 11
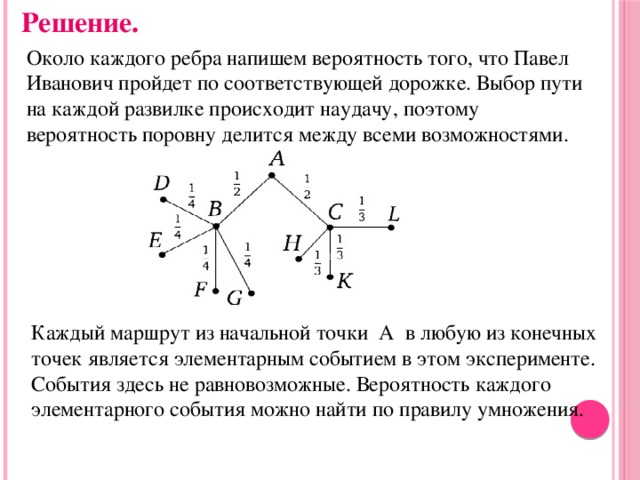
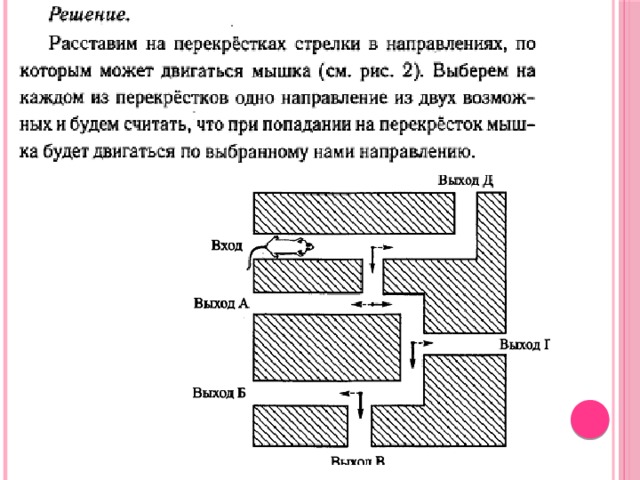
Решение.
Около каждого ребра напишем вероятность того, что Павел Иванович пройдет по соответствующей дорожке. Выбор пути на каждой развилке происходит наудачу, поэтому вероятность поровну делится между всеми возможностями.

Каждый маршрут из начальной точки A в любую из конечных точек является элементарным событием в этом эксперименте. События здесь не равновозможные. Вероятность каждого элементарного события можно найти по правилу умножения.
СЛАЙД 12

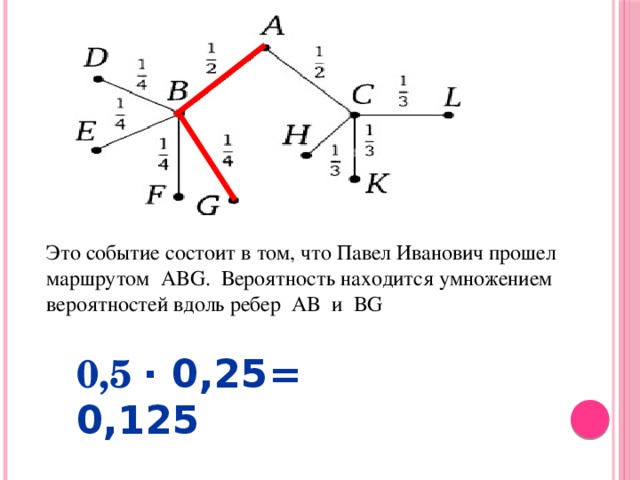
Это событие состоит в том, что Павел Иванович прошел маршрутом ABG. Вероятность находится умножением вероятностей вдоль ребер AB и BG
0,5 · 0,25= 0,125
СЛАЙД 13
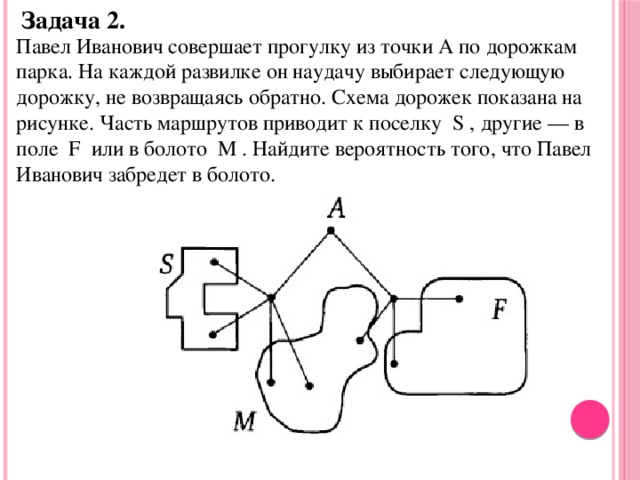
Задача 2.
Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S , другие — в поле F или в болото M . Найдите вероятность того, что Павел Иванович забредет в болото.
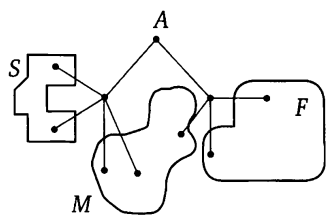

СЛАЙД 14
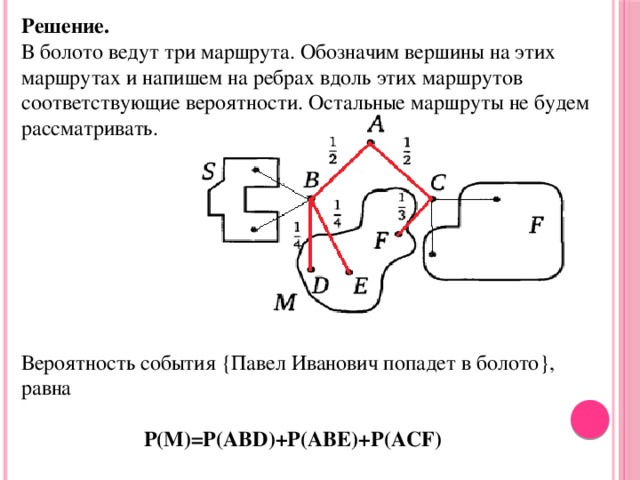
Решение.
В болото ведут три маршрута. Обозначим вершины на этих маршрутах и напишем на ребрах вдоль этих маршрутов соответствующие вероятности. Остальные маршруты не будем рассматривать.
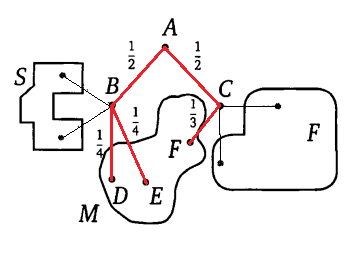
Вероятность события {Павел Иванович попадет в болото}, равна
P(M)=P(ABD)+P(ABE)+P(ACF)
СЛАЙД 15
СЛАЙД 16

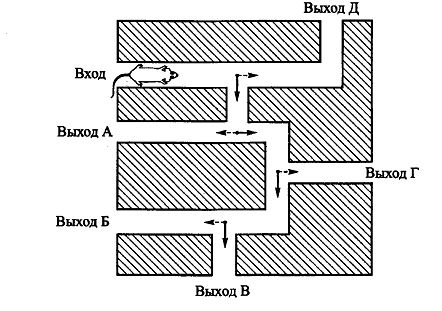
СЛАЙД 17


СЛАЙД 18
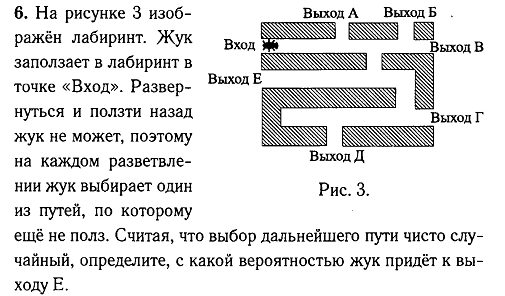
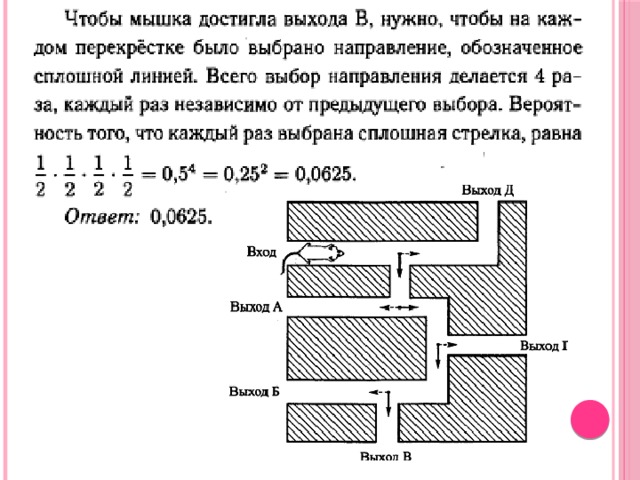
Ответ: 0,125
СЛАЙД 19, 20
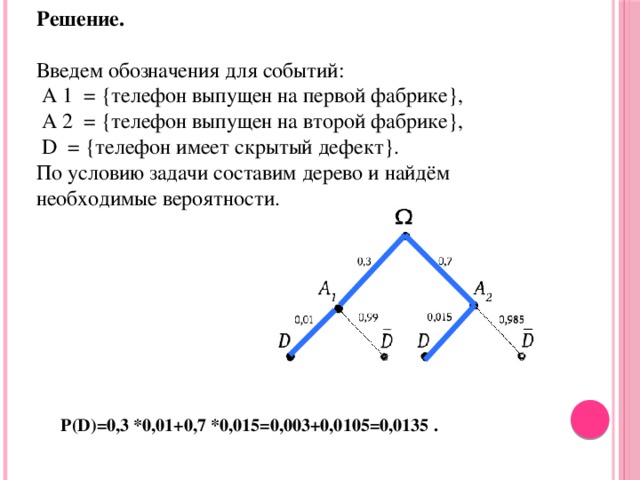
Задача 4.
Две фабрики одной фирмы выпускают одинаковые мобильные телефоны.
Первая фабрика выпускает 30 % всех телефонов этой марки, а вторая — остальные телефоны.
Известно, что из всех телефонов, выпускаемых первой фабрикой, 1 % имеют скрытые дефекты, а у выпускаемых второй фабрикой — 1,5 %.
Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.