Обучающие дидактические материалы по теме
«Логарифмическая функция».
ПОНЯТИЕ ЛОГАРИФМА
Перед изучением этой темы повтори тему «Степени»
Вспомни названия: 32 . Здесь 2-показатель степени, 3-основание.
3 . Здесь 3-показатель степени, 2-основание
Логарифмом числа b по основанию a называется показатель
степени , в которую надо возвести число a , чтобы получить b .
Обозначение log a b
b – может быть любым положительным числом, а может быть любым
положительным числом кроме единицы.
Пр.1: 2 3 =8.
3 – показатель степени , в которую надо возвести число 2 , чтобы
получить число 8, значит число 3 называется логарифмом числа 8 по
основанию 2 . 3 = loq 2 8
Вернись к определению, прочитай его.
Не понятно – смотри следующий пример
Пр.2: 3 2 = 9 .
2 – показатель степени, в которую надо возвести число 3 , чтобы
получить 9, значит число 2 называется логарифмом числа 9 по
основанию 3. 2 = log 3
Вернись к определению, прочитай его.
Не понятно – смотри следующий пример
Пр.3: 4 2 = 16
2 – показатель степени , в которую надо возвести число 4 , чтобы получить 16,
значит число 2 называется логарифмом числа 16 по основанию 4 .
2 = log 4 16
Вернись к определению, прочитай его.
Не понятно – смотри следующий пример.
Пр.4: 5 -1 =
-1 - показатель степени , в которую надо возвести число 5, чтобы получить
значит число -1 называется логарифмом числа
-1=log 5
Теперь от чисел перейдем к буквенным обозначениям
a c = b
с – показатель степени , в которую надо возвести число а , чтобы
получить b , значит число c называется логарифмом числа b по основа-
нию а .
с = log a b логарифмируемое число
логарифм основание
Вернись к определению, если не понятно – рассмотри еще раз примеры:
Уровень А
1. Вычислить 2 16
Чтобы вычислить логарифм числа 16 по основанию 2, надо ответить
на вопрос: в какую степень нужно возвести число 2, чтобы получить 16
Ответ: в четвертую, т.к. 24 = 2∙2∙2∙2 =16.
Следовательно логарифм числа 16 по основанию 2 равен 4.
Ответ: loq2 16=4
Вычислить
Чтобы вычислить логарифм числа
на вопрос: в какую степень нужно возвести число
Ответ: в третью, т.к.
рифм
Ответ:
3. Вычислить log15 1
Вопрос: в какую степень надо возвести число 15, чтобы получить 1
Ответ: в нулевую, т.к. 150 = 1, следовательно логарифм числа 1 по
основанию 15 равен 0.
Ответ: log15 1 = 0
Вычисли самостоятельно:
4.log 2 64 5.log3 81 6.log0,5 1 7.log 3 3
8.log5 125 9.log
12.log4 16 13.log4 64 14.log3 27 15.log11 121
16.log3 19.log0,5 0,25
20.log2 (-4) 21.log(-2) 8 22.log1 4 23.log0 3
ЗАПОМНИ
Логарифм отрицательного числа не существует.
Логарифм нуля не существует.
Логарифм по отрицательному основанию не существует.
Логарифм по основанию равному нулю не существует.
Логарифм по основанию равному единице не существует.
24. Вычислить log3 27+log2
Отдельно вычислим log3 27 и log2 , потом сложим их:
log3 27=3, log2 =-1, значит log3 27 + log2 =3+(-1)=3-1=2
Вычисли самостоятельно:
25. log5 log4 64
27. Запиши равенство 62 =36, применяя знак логарифма.
2 – это показатель степени, в которую надо возвести
число 6, чтобы получилось 36, значит 2 – это лога-
рифм числа 36 по основанию 6. Запишем ответ 2=log6 36.
Запиши следующие равенства, применяя знак логарифма:
28. 34 =81 29. 25 =32 30. 53 =125
31. Запиши равенство log4 16=2, не применяя знак
логарифма.
Если число 4 возвести во вторую степень, то
получится 16, значит можно записать 42 =16.
Запиши следующие равенства, не применяя знак
логарифма:
32. log2 32=5 33. log4 64=3 34. log4 1=0
Уровень Б
35. Вычислить log2
Т.к. 16=24, то вместо
По формуле х получим
Значит, чтобы получить 2 нужно возвести число 2 в
степень
Решение можно оформить так:
log2 2 =log2 2
Ответ: log2 =
36. Вычислить log3
Т.к. 243=35 , то
значит - (по формуле
следовательно искомый логарифм равен -
Решение можно оформить так:
log3 log3 = log3 = log3 3- = -
Ответ: log3 =-
Вычисли самостоятельно:
37. log
40. log4
43. log0,5 26 45. log
В более сложных случаях можно вычислять логарифмы
с помощью перехода к показательному уравнению.
Повтори решение показательных
уравнений способом приведения обеих частей
уравнения к степеням с одинаковым основанием
46. Вычислить log4 8
Трудно сразу ответить на вопрос: в какую степень нужно
возвести число 4, чтобы получилось 8. Показатель степени,
который будем вычислять, обозначим х. Получим
log4 8=х. Подобно тому, как вместо равенства log3 9=2 можно
записать 32 =9 , вместо равенства log4 8= х
запишем 4х =8.
Приведем обе части уравнения к степеням с
одинаковыми оснаниями
4х =8,
22х =23 .
Приравнивая показатели, получим
2х=3, х=
следовательно log4 8=
Ответ: log4 8=
47. Вычислить log16 32
Трудно сразу ответить на вопрос: в какую степень надо воз-
вести число 16, чтобы получить 32. Поэтому искомый лога-
рифм обозначим через х, получим log16 32=х.
Подобно тому, как вместо равенства log3 9=2 можно запи-
сать32 =9 , вместо равенства log16 32=х запишем 16х =32.
Решим это уравнение 16х =32.
Приведем обе части уравнения к степеням с одинаковыми
основаниями, получим
(24 )х =25 , 24х =25 , 4х=5, х=, следовательно log16 32 =
Ответ: log16 32 =
С помощью показательного уравнения легко
вычислить любой логарифм.
Вычисли самостоятельно:
48. log25 125 49. log8 128 50. log27 81 51. log64
52. Вычислить log3 log2 8
Cначала вычислим «внутренний» логарифм log2 8
log2 8=3
Теперь на месте log2 8 напишем число 3, получим
log3 log2 8=log3 3=1
Ответ: 1.
53. Вычислить2log4 log0,5 0,25
Сначала вычислим «внутренний» логарифм log0,5 0,25
log0,5 0,25=2
Теперь на месте log0,5 0,25 напишем число 2, получим
2log4 log0,5 0,25=2log4 2,
найдем log4 2=2 )
Умножим 2 на
Решение можно оформить так:
2log4 log0,5 0,25=2log4 2=2∙
Ответ: 1.
Вычисли самостоятельно:
54. log2 log3 81 55. log27 log10 1000
56. log5 125 57. log
58. Выяснить, при каких значениях х имеет
смысл выражение log7 (х-3)
Если ты забыл, как решаются неравенства,
повтори эту тему самостоятельно
Число 7 в любой степени положительно, значит на
месте х-3 должно быть положительное число,
получим х-30, х3.
Ответ: х3.
59. Выяснить, при каких значениях х имеет смысл
выражение logх
Логарифмируемое выражение должно быть поло-
жительным, значит 2х-40; основание логарифма
должно быть числом положительным и не равным
единице, значит х0, х≠1. Причем, все эти условия
должны выполняться одновременно, значит можно
записать систему неравенств
х0
х≠1
Решим первое неравенство 2х-40, получим
2х4, x2.
0 1 2 х
Выясни, при кaких значениях x имеет смысл выраже-
ние:
60. log13 (x2 +x-6)
Уровень В
Выясни, при кaких значениях x имеет смысл выраже-
ние:
61. log0,7 (x3 +x2 -2x) 62. logx-2 (2x-1).
Вычисли:
63. log625 0,625 64. log
66. log
ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВО
Пр1: Рассмотрим равенство 23 =8
Т.к. 3=log2 8, то в равенстве 23 =8 на месте числа 3
напишем log2 8. Получим
2 log 8 =8.
23 =8 и 2 log 8 =8 одно и то же.
Пр2: Рассмотрим равенство 42 =16
Т.к. 2= log4 16, то в равенстве 42 =16 на месте числа 2
напишем log4 16. Получим
4 log 4 16 =16.
Видим, что 42 =16 и 4 log 4 16 =16 одно и то же.
Перейдем к буквенным обозначениям .
Рассмотрим равенство a c = b
Т.к. c = log a b , то на месте с в равенстве a c = b
напишем loga b, получим
а log = b
это основное логарифмическое тождество. С его
помощью можно упрощать логарифмические выра-
жения и находить их значения.
Вычислить 3log 17
На месте а, число 3, на месте b, под знаком логарифма
число 17, значит и после знака равенства, используя фор-
мулу а log = b , напишем число 17, получим
3log 17 =17
Вычислить 0,7log 44
На месте а, число 0,7 , на месте b, под знаком логариф-
ма, число 44, значит и после знака равенства, используя фор-
мулу а log = b , напишем число 44, получим
0,7log 44 =44.
3. Вычислить самостоятельно:
7 log 3 4. 13 log 11 5. 39 log 27 6. 27log
7. Вычислить 8 log 3
Сразу воспользоваться формулой а log =b нельзя.
Сначала вместо числа 8 напишем 23 , получим
8 log 3 =23 log 3
Т.к. показатели перемножаются при возведении
степени в степень (формула (хm )n =xm ∙ n ), то можно
записать 23 log 3 =(2 log 3 )3 .
В скобке, по формуле а log b , получим 2 log 3 =3.
Т.к. «скобка была в третьей степени», то полученное
число 3 возведем в третью степень, получим 27.
Решение можно оформить так:
8 log 3 = 23 log 3 =( 3 =33 =27.
Ответ: 27
Вычисли самостоятельно:
8. 9 log 7 9. 4log 5 10. 81log 2 11. log 27
Уровень Б
12. Вычислить 0,5log 9
Сначала число 0,5 представим как 4 в степени,
получим 0,5=-1 =(-1 =(4-1 =4
0,5log 9 =4
13. Вычислить 10log 7+3
Т.к. показатели складываются при умножении степеней
с одинаковым основанием (формула хm xn =xm + n ) , то получим
10log 7+3 =10log 7 ∙103 =7∙ 1000=7000
Ответ: 7000.
Вычисли самостоятельно:
14. 7log 15. log 16. 9log
17. -log 18. 9-2log 19. log 3 5
20. 0,027 log 4 21. 163 log 21 22. 12
23.
ПРОВЕРЬ СЕБЯ
Уровень А
Запиши следующие равенства, применяя знак лога-
рифма .
1. 63 =36 2. 45 =1024 3. 0,14 =0,0001
4. 3 =-5 =
Запиши следующие равенства , не используя знак
логарифм:
6. log2 8=3. 7. log2 =-3 8. log
9. log2 1024=10 10. log
Вычисли
11. log
14. lg100 15. log7 49 16. log4 64
17. log3 243+lg1000 18. log9 81+log5 125
19. 11
22. 9
Вместо знака «?» поставь число
Например: 25. logх 4=2
На месте х должно стоять число, которое
возводится во вторую степень и получается 4,
это число 2, т.к. 22 =4, запишем ответ log2 4=2.
26. logх 8=3 27. logх 16=4 28. logх 27=3
29. logх 25=2 30. logх 49=2 31. log3 х=3
log4 х=2 33. log6 х=1
Уровень Б
Вычисли:
34. log4 35. log5 36. log
37. log5 0,008 39. log
40. log0,5 832 128 42. log27 243
43. log128 46. log
46. log
49.
52. 0,125
55.
58. log3 log2 8 59. 2log27 log1000 10
60. log4 log16 256+log4 8
61. 9 log2 8+3log2 log4 16+log
Выясни, при каких значениях х существует
логарифм:
62. log3 (5-x) 63. log3 (x-5) 64. log11 (-x)
65. log7 (49-x2 ) 66. log4 (x2 +4) 67. log6
Уровень В
Вычисли:
68. 32
71. (tg60º)
Выясни, при каких значениях х существует
логарифм:
73. log13 (1-x3 ) 74. logx -1 (x2 -1)
ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
Десятичный логарифм – это логарифм числа по
основанию 10.
Обозначение: вместо log10 b пишут lgb, т.е. log10 b= lgb
Например: вместо log10 3 пишут lg3, т.е. log10 3=lg3,
вместо log10 0,5 пишут lg0,5, т.е. log10 0,5=lg0,5
Натуральный логарифм – это логарифм числа по
основанию e , e ≈ 2,7.
Обозначение: вместо log e e
Например: вместо log e e
вместо log e e
Существует формула, которая позволяет перейти от
логарифма по одному основанию к логарифму по другому
основанию loga b =
1. Выразить log5 3 через логарифм по основанию 7.
Задание следует понимать так: нужно перейти от
логарифма по основанию 5 к логарифму по основанию 7.
Для этого подставим в формулу loga b =
место a число 5, на место b число 3, на место d число 7,
получим log5 3=
Ответ: log5 3 =
2. Выразить log5 17 через натуральный логарифм.
Для этого подставим в формулу loga b =
место a число 5, на место b число 17, на место d число e ,
получим log5 17=
Ответ: log5 17=
Уровень А
Вырази следующие логарифмы через
десятичные логарифмы:
3. log15 12 4. log12 100 5. log3 25
Вырази следующие логарифмы через
натуральные логарифмы:
6. log3 18 7. lg8 8. lg11
Уровень Б
9. Дано: log7 2=m. Найти: log49 28
log49 28 выразим через логарифм по основанию 7,
получим log49 28=
числитель и знаменатель этой дроби:
1) числитель: log7 28= log7 (7∙4)= log7 7+ log7 4=1+ log7 22 =
=1+2log7 2=1+2m;
2) знаменатель: log7 49=2
3) разделим числитель на знаменатель, получим
Ответ:
Самостоятельная работа
Вариант 1
Решите уравнения:
log 3 (2x – 1) = 2;
log0,2 (12x + 8) = log0,2 (11x + 7);
lg2 x2 + lgx2 – 6 = 0;
Xlog 0,5 x =
log10 x + log x + … + log x = 5,5.
Ответы: 1. 5;
2. решений нет;
3.
4. 0,25; 4;
5.
Вариант 2
Решите уравнения:
1. ln(3x – 5 ) = 0;
2. log 6 (2x2 – x) = 1 – log 6 2;
3. Xlog 2 x = 16;
4. 3log2 2 x + 2log2 x = 5;
5. log10 x + log x + … + log x = 5,5.
Ответы: 1. 2; 3. 0,25; 4;
1,5; - 1; 4. 2;
Приложение 3
Задание по вариантам
В1 В4
1.log2 (3x-6)=log2 (2x-3); 1.log4 (x + 3) = 4;
2.log3 2 x – 5log3 x = 7;
3.log2 2 x – 4log2 x + 3 = 0; 3.lg(x2 – 6) = lg(8 + 5x);
4.log2 x = log2 3 + log2 5; 4.log
5.xlog 3 x = 9. 5. .xlog 3 x = 3.
В 2. В5
1.log0,5 2 x + 3log0,5 x + 2 = 0; 1.log0,2 (12x + 8) = log0,2 (11x + 7);
2.log7 4 = log7 x – log7 9; 2.log5 x = 2;
3.log6 (14 – 4x) = log6 (2x + 2); 3.3log4 2 x – 7log4 x + 2 = 0;
4.log3 x = 2 x = log2 3 + log2 5;
5.xlog 3 x = 81. 5.xlog 3 x = 143.
в 3
1.lg2 x2 + lgx2 = 6;
2.log3 (x2 + 6) = log3 5x;
3.log2 x = -0,5;
4.log
5. .xlog 3 x = 27.
Приложение 4
Задание 1
Решите уравнение
1. 2.
3. . 4 .
5 . . 6 .
7 . . 8 . .
9. 10 .
11.
Задание 2
Решите уравнение
12. 13.
14.
15. . 16
Задание 3
Решите уравнение
17 . 18 .
19 . 20 .
21 .
22 .
23. .
Задание 4
Решите уравнение
24. 5 .
26. 7.
28. 9.
30. .
Ответы к заданиям по теме "Логарифмические уравнения"
К заданию 1
1 . 19. 2. 1. 3 . 2. 4 . 5 .
6. 1. 7. . 8 . 3. 9 . 0; 2. 10 . 0; 3. 11 . 2; 4.
К заданию 2
12. 2. 13 . 14 . -1. 15 . 36. 16 . 48.
К заданию 3
17 . 64. 18 . 1,5. 19 . 22 . 3. 23 .
К заданию 4
-1; 2. 25 . 6 . 0,1; 1000. 27 . 2. 28 . 9 . 0 . 5.
П риложение 5
Упражнения
Решите уравнения:
62. 63.
64. 65.
66. 67.
68. 69.
70. . 71 .
72. 73.
74.
75.
76.
77. 78 .
79.
Ответы
62 . 63. -3. 64. 65. 66. 8. 67. 68. -4. 69. 70.
71. 9. 73. 8. 74. . 75. ; 1. 76. 3. 77. 16. 78. 79.
Литература
1. Багманов А. Т., Иванов Л. А., Толстых И. В. Математика. Избранные задачи. Абитуриенту - 2002 для самостоятельной работы. - СПб. Из-во СПбГТУ, 2002. 150 с.
Болтянский В. Г., Ю. В. Сидоров, М. И. Шабунин «Лекции и задачи по элементарной математике», Москва «Наука», 1971 г.
Гальперин Г. А., А. К. Толпыго «Московские математические материалы», под ред. А. Н. Колмогорова, Москва «Просвещение», 1986 г.
Доброва О. Н. «Задания по алгебре и математическому анализу», Москва «Просвещение», 1996 г.
Егорова А. А. «Практикум абитуриента». Алгебра и тригонометрия. Приложение к журналу «Квант» 3, 1995 г., Москва, 1995 г., бюро «Квантум».
Зорин В. В. «Пособие по математике для поступающих в вузы», Москва «Высшая школа», 1965 г.
Новые педагогические и информационные технологии в системе образования: Учеб. пособие для студ. педагогических ВУЗов и системы повыш.квалификации пед. кадров /Е.С. Полат, М.Ю. Бухаркина и др.; Под ред. Е.С. Полат. – М.: Издательский центр «Академия», 2000.
9. Селевко Г.К. Современные образовательные технологии: Уч. пособие. – М.:
Народное образование, 1998.
10. Колмогоров А. Н. Алгебра и начала анализа. Уучебник для 10-11 классов, общеобразовательных учреждений. Москва «Просвещение»2003.
11. Тишин В. И. Математика для учитилей и учащихся 2002.
 23. Здесь 3-показатель степени, 2-основание
23. Здесь 3-показатель степени, 2-основание
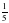



 loq
loq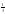
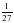
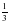 надо ответить
надо ответить 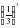 =
= 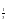
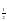
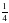 10.log
10.log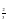
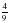 11.log
11.log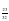
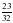
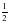
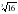
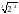 .
. 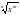 =х
=х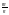 получим
получим















