Методические рекомендации по развитию логического мышления младших школьников

Пояснительная записка

В современном обществе перед педагогами остро стоит задача развития талантливых детей, так как от притока талантливых исследователей зависит развитие науки. Поэтому так важно уже в на­чальной школе поддерживать интерес детей к знаниям, выявляя осо­бо одаренных учеников. Ведь именно в этот период проявляются и активно развиваются склонности, способности, таланты. Именно в это время происходят первые самостоятельные открытия ребенка. Пусть они даже небольшие и как будто незначительные, но в них — ростки будущего интереса к науке. Реализованные возможности развивают ребенка, стимулируют интерес к различным наукам.

В младшем школьном возрасте происходит интенсивное развитие интеллекта детей. Развиваются и превращаются в регулируемые произвольные процессы такие психические функции, как мышление, восприятие, память.

К 8-9-летнему возрасту у ребенка происходит переход к стадии формальных операций, которая связана с определённым уровнем развития способности к абстрагированию (умение выделять существенные признаки предметов и отвлечься от второстепенных признаков предметов) и обобщению. Критерием овладения тем или иным понятием является умение им оперировать.

Особые трудности возникают у младших школьников при установлении причинно-следственных связей. Младшему школьнику легко устанавливать связь от причины к следствию, чем от следствия к причине. Это можно объяснить тем, что при умозаключении от причины к следствию устанавливается прямая связь. А при умозаключении от факта к вызвавшей его причине такая связь непосредственно не дана, так как указанный факт может быть следствием самых разных причин, которые нужно специально анализировать.

Чтобы помочь младшим школьникам, следует предлагать на каждом уроке и во внеурочной деятельности, упражнения, задания, игры, которые способствовали бы развитию логического мышления. Необходимо на уроках предлагать детям задачи и упражнения с нестандартным решением. Постоянно предлагая детям такие задания, мы учим их чётко и ясно мыслить, рассуждать, спорить, доказывать.

Использование нестандартных заданий способствует развитию мыслительных операций, таких как обобщение, анализ, синтез, сравнение, классификация, абстрагирование.

Используя на уроках такие виды заданий, я заметила, что учащиеся с интересом выполняют предложенные задания, лучше усваивают учебный материал, таким образом, процесс обучения математике не сводится только к вычислительным действиям, а становится основой развития личности ребёнка.

Развивая логическое мышление школьников, мы способствуем и развитию познавательного интереса и способностей, свойственных практически всем детям в раннем возрасте. Тренируя ум, человек становится наблюдательным, сообрази­тельным, проницательным, догадливым, дальновидным, изобре­тательным, находчивым, остроумным, а также приобретает мно­гие другие важные и полезные качества, которые все вместе составляют культуру мышления, или умственную культуру.

1

2

Особенности развития мышления младших школьников

Термин «логика» происходит от греческого слова «логос», что означает «мыслить», «разум». Логика – есть наука о законах и формах правильного мышления. Она изучает формы рассуждений, отвлекаясь от конкретного содержания, устанавливает, что из чего следует, ищет ответ на вопрос: как мы рассуждаем? Основоположником логики как науки является древнегреческий философ и ученый Аристотель. Он впервые разработал теорию логического вывода.

Психолог Л.С. Выготский отмечал интенсивное развитие интеллекта детей в младшем школьном возрасте. Развитие мышления приводит, в свою очередь, к качественной перестройке восприятия и памяти, превращению их в регулируемые, произвольные процессы.

Ребёнок 7-8 лет мыслит конкретными категориями. Затем происходит переход к стадии формальных операций, которая связана с определенным уровнем развития способности к обобщению и абстрагированию.

К моменту перехода в среднее звено школы (5 класс) школьники должны научиться самостоятельно рассуждать, делать выводы, сопоставлять, сравнивать, анализировать, находить частное и общее, устанавливать простые закономерности.

Ребенок, начиная обучаться в школе, должен обладать достаточно развитым логическим мышлением. Чтобы сформировать у него научное понятие, необходимо научить его дифференцированно подходить к признакам предметов. Надо показать, что есть существенные признаки, без наличия которых предмет не может быть подведён под данное понятие.

За время обучения в начальном звене ребёнок, прежде всего, должен познакомиться с понятиями, с их существенными и несущественными признаками.

Поэтому первый этап в развитии теоретического мышления младших школьников может быть назван следующим образом: знакомство с признаками понятий.

На втором этапе нужно сформировать умение оперировать существенными признаками понятий, опуская признаки несущественные, то есть речь идёт о формировании такой операции логического мышления, как абстрагирование.

На третьем этапе необходимо самое серьёзное внимание обратить на формирование логической операции сравнения с опорой на существенные и несущественные признаки предметов и явлений. При формировании этой операции логического мышления следует особое внимание обратить на поиск общих и отличительных признаков понятий, предметов и явлений.

Первые три этапа реализуются в 1-2 классах начальной школы.

На четвёртом этапе (3 класс) школьники должны научиться выстраивать иерархию понятий, вычленять более широкие и более узкие понятия, находить связи между родовыми и видовыми понятиями. К этому этапу развития логического мышления можно

3

отнести и формирование умение давать определение понятиям на основе умения находить более общее родовое понятие и видовые отличительные признаки.

Пятый этап (4 класс) предполагает развитие аналитической деятельности, которая вначале (1-2 класс) заключается в анализе отдельного предмета (поиск признаков), а к 3-4 классу в умении анализировать связи между предметами и явлениями (часть и целое, рядоположенность, противоположность, причина и следствие, наличие тех или иных функциональных отношений и другое).

К окончанию младшей школы у ребенка должны быть сформированы такие операции логического мышления, как обобщение, классификация, анализ и синтез.

В связи с относительным преобладанием деятельности первой сигнальной системы у младших школьников более развита наглядно-образная память. Дети лучше сохраняют в памяти конкретные сведения, лица, предметы, факты, чем определения и объяснения. Они часто заучивают дословно. Это объясняется тем, что механическая память развита у них хорошо и младший школьник ещё не умеет дифференцировать задачи запоминания (что надо запомнить дословно, а что в общих чертах), ребёнок ещё плохо владеет речью, ему легче заучить всё, чем воспроизвести своими словами. Дети ещё не умеют организовывать смысловое запоминание: не умеют разбивать материал на смысловые группы, выделять опорные пункты для запоминания, составлять логический план текста.

Под влиянием обучения память у детей в младшем школьном возрасте развивается в двух направлениях:

- усиливается роль и удельный вес словесно-логического запоминания (по сравнению с наглядно-образным);

- формируется возможность сознательно управлять своей памятью и регулировать её проявления (запоминание, воспроизведение, припоминание). Развитие словесно-логической памяти происходит в результате развития логического мышления.

К переходу в среднее звено у учащегося должна сформироваться способность к запоминанию и воспроизведению смысла, существа материала, доказательств, аргументации, логических схем, рассуждений. Очень важно научить школьника правильно ставить цели для запоминания материала. Именно от мотивации зависит продуктивность запоминания. Если ученик запоминает материал с установкой, что этот материал понадобится в скором времени, то материал запомнится быстрее, помнится дольше, воспроизводится точнее.

Восприятие становится думающим

В процессе обучения в начальном звене школы восприятие ребёнка становится:

а) более анализирующим;

б) более дифференцирующим;

в) принимает характер организованного наблюдения;

4

г) изменяется роль слова в восприятии (если у первоклассников слово по преимуществу несёт функцию названия, т.е. является словесным обозначением после узнавания предмета, у учащихся более старших классов слово-название уже является самым общим обозначением объекта, предшествующим более глубокому его анализу).

Развитие восприятия не происходит само собой, а идёт параллельно с развитием мышления.

Одним из наиболее эффективных методов организации восприятия и воспитания наблюдательности является сравнение. Развивая у ребёнка такую мыслительную операцию, как сравнение, делаем его восприятие более глубоким. При этом количество ошибок восприятия уменьшается.

Внимание становится произвольным

Возможности волевого регулирования внимания у учащихся 1-2 классов весьма ограничены. В этом возрасте у детей преобладает непроизвольное внимание. Если старший школьник может заставить себя сосредоточиться на неинтересном, на трудной работе ради результата, который ожидается в будущем, то младший школьник обычно может заставить себя сосредоточиться, упорно работать лишь при наличии "близкой" мотивации (перспективы получить пятёрку, заслужить похвалу учителя).

Воспитание у младших школьников "далёкой" мотивации произвольного внимания должно происходить в соответствии с возрастными особенностями, путём связывания друг с другом близких и всё более отдалённых целей. Непроизвольное внимание становится особенно концентрированным и устойчивым тогда, когда учебный материал отличается наглядностью, яркостью, вызывает у младших школьников эмоциональное восприятие. Поскольку непроизвольное внимание поддерживается интересом, то, естественно, уроки и занятия с детьми должны быть увлекательными и занимательными.

Формируется способность к саморегуляции

На данном этапе такие качества, как произвольность и способность к саморегуляции, рефлексия, проходят только начальный этап формирования. Затем они усложняются и закрепляются. Сначала эти качества распространяются только на ситуации, которые связаны с учёбой, а затем и на другие сферы деятельности ребёнка.

Формируется интерес к содержанию учебной деятельности, приобретению знаний

К моменту перехода из начальной школы в среднее звено изменяется отношение к учёбе. Сначала у первоклассников формируется интерес к самому процессу учебной деятельности (они могут старательно делать то, что им в жизни никогда не пригодится, например, срисовать японские иероглифы).

Затем формируется интерес к результату своего труда: мальчик на улице самостоятельно прочитал вывеску, был очень рад.

5

После возникновения интереса к результатам своего учебного труда у первоклассников формируется интерес к содержанию учебной деятельности, потребность приобретать знания. Это связано с переживанием школьниками чувства удовлетворения от своих достижений. А стимулирует это чувство одобрение учителя, взрослого, подчёркивание даже самого небольшого успеха, продвижения вперёд.

Младшие школьники испытывают чувство гордости, особый подъём сил, когда учитель, поощряя их и стимулируя их желание работать лучше, говорит: "Вы работаете теперь не как маленькие дети, а как настоящие ученики!"

Даже относительные неудачи полезно комментировать примерно таким образом: "Ты уже пишешь гораздо лучше. Сравни, как ты пи сал сегодня и как писал неделю назад. Молодец! Ещё немного усилий – и ты будешь писать так, как надо".

Происходит осознание личного отношения к миру

Сначала этот фактор затрагивает учебную сферу как более знакомую детям. Переход в среднее звено стимулирует этот процесс формирования личного отношения к учению, но не все дети оказываются готовы к нему. В результате может сформироваться "мотивационный вакуум", который характеризуется тем, что прежние представления уже не устраивают детей, а новые ещё не осознались, не оформились.

Складывается характер

Характер младшего школьника имеет следующие особенности: импульсивность, склонность незамедлительно действовать, не подумав, не взвесив всех обстоятельств (причина – возрастная слабость волевой регуляции поведения); общая недостаточность воли (школьник 7-8 лет ещё не умеет длительно преследовать намеченную цель, упорно преодолевать трудности); капризность, упрямство (объясняются недостатками семейного воспитания). Ребёнок привык, чтобы все его желания и требования удовлетворялись. Капризность и упрямство – своеобразная форма протеста ребёнка против тех твёрдых требований, которые ему предъявляет школа, против необходимости жертвовать тем, что "хочется", во имя того, что "надо".

К окончанию начальной школы у ребёнка формируется трудолюбие, аккуратность, прилежание, дисциплинированность.

Постепенно развивается способность к волевой регуляции своего поведения, формируется умение сдерживать и контролировать свои поступки, не поддаваться непосредственным импульсам, растёт настойчивость. Ученик 3-4 класса способен в результате борьбы мотивов отдавать предпочтение мотиву долженствования.

В целом за время обучения ребёнка в начальном звене школы у него должны сформироваться следующие качества: произвольность, рефлексия, мышление в понятиях; успешное освоение программы; основные компоненты учебной деятельности; качественно новый, более "взрослый" тип взаимоотношений с учителями и одноклассниками.

Если говорить о настоящем состоянии современной начальной школы, то основное место все еще продолжает занимать репродуктивная деятельность. На уроках математики дети почти все время решают учебно-тренировочные типовые задания. Их назначение состоит в

6

том, чтобы поисковая деятельность детей с каждой последующей задачей постепенно свертывалось, это тормозит развитие интеллекта детей, в первую очередь, мышления. В связи с этой системой преподавания дети привыкают решать задачи, которые всегда имеют готовые решения, причем, как правило, только одно решение. Поэтому дети теряются в ситуациях, когда задача не имеет решения, или, наоборот, имеет несколько решений. Кроме того, дети привыкают решать задачи на основе уже выученного правила, поэтому они не могут действовать самостоятельно.

Систематическое использование на уроках математики и внеурочных занятиях специальных упражнений и заданий, направленных на развитие логического мышления, расширяют кругозор младших школьников, позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности.

Работая над развитием логического мышления на уроках математики, заметила, что при выполнении самостоятельных работ даже слабые ученики рассуждают, выделяют вопрос.

В ходе регулярных занятий у детей формируются не только познавательные способности, но и качества личности как выдержка, настойчивость, трудолюбие, честность.

Нужно помнить, что последовательность и систематичность в работе с детьми – залог успешного решения поставленных задач.

Приемы развития логического мышления

1) Логические задачи.

Вася выше Саши на 8 см, а Коля ниже Саши на 3 см. На сколько сантиметров

самый высокий из мальчиков выше самого маленького?

2) «Магические квадраты».

- расставьте числа 2; 4; 5; 9; 11; 15 так, чтобы по всем линиям в сумме получилось 24.

3) Сравни уравнения в каждом столбике и, не вычисляя, скажи, в котором из

них неизвестное число больше. Проверь вычислением:

х + 37 = 78 90 – х = 47 х – 28 = 32 45 + х = 63

х + 37 = 80 90 – х = 50 х – 28 = 22 45 + х = 68

Развитию мышления способствует так же применение различных приемов работы над задачей:

1. Решение задач различными способами.

2. Решение задач с недостающими или лишними данными.

3. Изменение вопроса задачи

4. Работа над решенной задачей.

5. Моделирование текста задач.

6. Представление ситуации, описанной в задаче (нарисовать "картинку").

7. Самостоятельное составление задач учащимися.

( используя слова больше на, столько, сколько, меньше в, на столько больше, на столько меньше).

7

8. Выбор математических выражений по данным условия задачи и объяснение, что обозначает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.

9. Объяснение готового решения задачи.

10. Использование приема сравнения текстов задач

11. Выбор верного решения из двух предложенных.

12. Изменение условия задачи в соответствии с данным решением.

13. Закончить решение задачи.

14. Выбор вопроса к данному условию? (обратный вариант – восстановить пропущенный вопрос и действие в задаче).

15. Составление аналогичной задачи с измененными данными.

16. Решение «обратных» задач.

Логические задачи.

Логические задачи - особый раздел по развитию словесно-логического мышления, включающий в себя целый ряд разнообразных упражнений.

Логические задачи предполагают осуществление мыслительного процесса, связанного с использованием понятий, логических конструкций, существующих на базе языковых средств.

В ходе такого мышления происходит переход от одного суждения к другому, их соотношение через опосредование содержания одних суждений содержанием других, и как следствие формулируется умозаключение.

Задачи для решения.

1. Саша ел яблоко большое и кислое. Коля ел яблоко большое и сладкое. Что в этих яблоках одинаковое? Разное?

2. Маша и Нина рассматривали картинки. Одна девочка рассматривала картинки в журнале, а другая девочка - в книжке. Где рассматривала картинки Нина, если Маша не рассматривала картинки в журнале?

3. Толя и Игорь рисовали. Один мальчик рисовал дом, а другой - ветку с листьями. Что рисовал Толя, если Игорь не рисовал дом?

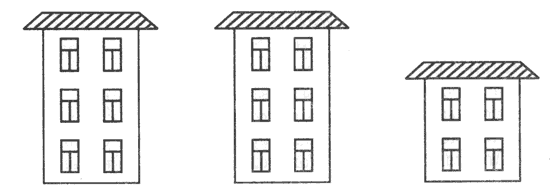
4. Алик, Боря и Вова жили в разных домах. Два дома были в три этажа, один дом был в два этажа. Алик и Боря жили в разных домах, Боря и Вова жили тоже в разных домах. Где жил каждый мальчик?

5. Коля, Ваня и Сережа читали книжки. Один мальчик читал о путешествиях, другой - о войне, третий - о спорте. Кто о чем читал, если Коля не читал о войне и о спорте, а Ваня не читал о спорте?

6. Зина, Лиза и Лариса вышивали. Одна девочка вышивала листочки, другая - птичек, третья - цветочки. Кто что вышивал, если Лиза не вышивала листочки и птичек, а Зина не вышивала листочки?

7. Мальчики Слава, Дима, Петя и Женя сажали плодовые деревья. Кто-то из них сажал яблони, кто-то - груши, кто-то - сливы, кто-то - вишни. Что сажал каждый мальчик, если Дима не сажал сливы, яблони и груши, Петя не сажал груши и яблони, а Слава не сажал яблони?

8. Девочки Ася, Таня, Ира и Лариса занимались спортом. Кто-то из них играл в волейбол, кто-то плавал, кто-то бегал, кто-то играл в шахматы. Каким спортом увлекалась

8

каждая девочка, если Ася не играла в волейбол, в шахматы и не бегала, Ира не бегала и не играла в шахматы, а Таня не бегала?

Эти восемь задач имеют три степени сложности. Задачи 1-3 - самые простые, для их решения достаточно оперировать одним суждением. Задачи 4-6 - второй степени сложности, поскольку при их решении необходимо сопоставить два суждения. Задачи 7 и 8 - самые сложные, т.к. для их решения нужно соотнести три суждения.

Обычно трудности, возникающие при решении задач с 4 по 8, связаны с невозможностью удержать во внутреннем плане, в представлении все обстоятельства, указанные в тексте, и они путаются, поскольку не пытаются рассудить, а стремятся увидеть, представить правильный ответ. Эффективен в этом случае прием, когда ребенок имеет возможность опираться на наглядные представления, помогающие ему удержать все текстовые обстоятельства.

Например, взрослый может сделать картинки домиков (задача № 4). А затем с опорой на них проводить рассуждение такого типа: "Если Алик и Боря жили в разных домах, то в каких из нарисованных они могли бы жить? А почему не в первых двух? и т.д.

К задачам 7 и 8 удобнее сделать таблицу, которая будет заполняться по мере рассуждения. Например, таблица к задаче №7:

ЯБЛОНИ ГРУШИ СЛИВЫ ВИШНИ

Слава

Дима - - - +

Петя

Женя

"Известно, что Дима не сажал сливы, яблони и груши. Следовательно, около этих деревьев рядом с Димой мы можем поставить прочерк. Тогда, что же сажал Дима? Правильно, осталась только одна свободная клеточка, т.е. Дима сажал вишни. Поставим в этой клетке знак "+" и т.д."

Графическое отражение структуры хода рассуждения помогает ребенку уяснить общий принцип построения и решения задач такого типа, что в последующем делает успешной мыслительную деятельность ребенка, позволяя справляться с задачами более сложной структуры.

Следующий вариант задач содержит следующее исходное положение: если даны три объекта и два признака, одним из которых обладают два объекта, а другим один, то, зная, какие два объекта отличаются от третьего по указанным признакам, можно легко определить, каким признаком обладают первые два. При решении задач подобного типа ребенок учится совершать следующие мыслительные операции:

9

- делать вывод об идентичности двух объектов из трех по указанному признаку. Например, если в условии сказано, что Ира и Наташа и Наташа с Олей вышивали разные картинки, то понятно, что Ира и Оля вышивали одинаковую;

- делать вывод о том, каков тот признак, по которому эти два объекта идентичны. Например, если в задаче сказано, что Оля вышивала цветок, следовательно, Ира тоже вышивала цветок;

- делать окончательный вывод, т.е. исходя из того, что уже известны два объекта из четырех, которые идентичны по одному из двух данных в задаче признаков, ясно, что другие два объекта идентичны по другому из двух известных признаков. Так, если Ира и Оля вышивали цветок, то другие две девочки, Наташа и Оксана, вышивали домик.

Задачи на сравнение.

В основе этого типа задач лежит такое свойство отношения величин объектов, как транзитивность, состоящее в том, что если первый член отношения сравним со вторым, а второй с третьим, то первый сравним с третьим.

Начинать обучение решению таких задач можно с самых простых, в которых требуется ответить на один вопрос и которые опираются на наглядные представления.

1. "Галя веселее Оли, а Оля веселее Иры. Нарисуй рот Иры. Раскрась красным карандашом рот самой веселой девочки.

Кто из девочек самый грустный?

1. "Волосы у Инны темнее, чем у Оли. Волосы у Оли темнее, чем у Ани. Раскрась волосы каждой девочки. Подпиши их имена. Ответь на вопрос, кто светлее всех?"

3. "Толя выше Игоря, Игорь выше Коли. Кто выше всех? Покажи рост каждого мальчика".

Графическое изображение транзитивного отношения величин значительно упрощает понимание логической структуры задачи. Поэтому, когда ребенок затрудняется, мы советуем использовать прием изображения отношения величин на линейном отрезке. Например, дана задача: "Катя быстрее Иры, Ира быстрее Лены. Кто быстрее всех?". В этом

10

случае объяснение может строиться следующим образом: "Посмотри внимательно на эту линию.

С одной стороны располагаются дети самые быстрые, с другой - медленные. Если Катя быстрее Иры, то где мы поместим Катю, а где Иру? Правильно, Катя будет справа, где быстрые дети, а Ира слева, т.к. она более медлительна. Теперь сравним Иру и Лену.

Мы знаем, что Ира быстрее Лены. Где мы тогда поместим Лену относительно Иры? Правильно, еще левее, т.к. она медленнее Иры.

Посмотри внимательно на чертеж. Кто же быстрее всех? а медленнее?".

Ниже мы приводим варианты логических задач, которые делятся по степени сложности на три группы:

1) задачи 1-12, в которых требуется ответить на один вопрос;

2) задачи 12-14, в которых нужно ответить на два вопроса;

3) задачи 15 и 16, решение которых предполагает ответ на три вопроса.

Условия задач различаются не только по количеству информации, в которой нужно разобраться, но и по ее наблюдаемым особенностям: виды отношений, разные имена, поставленный по-разному вопрос. Особое значение имеют "сказочные" задачи, в которых отношения между величинами построены таким образом, каких в жизни не бывает. Важно, чтобы ребенок смог отвлечься от жизненного опыта и пользовался теми условиями, какие даются в задаче.

Варианты задач.

1. Саша грустнее, чем Толик. Толик грустнее, чем Алик. Кто веселее всех?

2. Ира аккуратнее, чем Лиза. Лиза аккуратнее, чем Наташа. Кто самый аккуратный?

3. Миша сильнее, чем Олег. Миша слабее, чем Вова. Кто сильнее всех?

4. Катя старше, чем Сережа. Катя младше, чем Таня. Кто младше всех?

5. Лиса медлительнее черепахи. Лиса быстрее, чем олень. Кто самый быстрый?

6. Заяц слабее, чем стрекоза. Заяц сильнее, чем медведь. Кто самый слабый?

7. Саша на 10 лет младше, чем Игорь. Игорь на 2 года старше, чем Леша. Кто младше всех?

Все рассмотренные нами варианты логических задач направлены на создание условий, в которых существует или существовала бы возможность формирования способности выделять существенные отношения между объектами и величинами.

11

Кроме тех задач, которые были указаны выше, целесообразно предлагать ребенку задачи, в которых отсутствует часть необходимых данных или, наоборот, имеются ненужные данные. Можно также использовать прием самостоятельного составления задач по аналогии с данной, но с другими именами и иным признаком (если в задаче имеется признак "возраст", то это может быть задача про "рост" и т.д.), а также задач с недостающими и избыточными данными. Имеет смысл превращение прямых задач в обратные и наоборот. Например, прямая задача: "Ира выше Маши, Маша выше Оли, кто выше всех?"; в обратной задаче вопрос: "Кто ниже всех?".

Если ребенок успешно справляется со всеми видами предложенных ему задач, целесообразно предлагать задания, связанные с творческим подходом:

- придумать задачу, которая как можно более не похожа на задачу-образец, но построена по единому с ней принципу;

- придумать задачу, которая была бы сложнее, например, содержала бы больше данных, чем образец;

- придумать задачу, которая была бы проще, чем задача-образец, и т.д.

Полезны и занимательны игры со счетными палочкам. Они развивают у детей умение самостоятельно осуществлять поиск способа решения. В этих играх содержатся задания на преобразование одних фигур в другие. Для их решения надо ставить фигуру по отдельным условиям или видоизменить ее: переложить, убрать указанное количество палочек с целью получения новой фигуры той же структуры, но с другим количеством квадратов или треугольников.

Более простыми являются задания на составление фигуры из палочек.

1. Составить из пяти палочек флажок; лопатку; два равных треугольника и

один четырехугольник.

Из шести палочек – домик, прямоугольник.

В результате практических поисков дети приходят к какому-то решению (со-

ставить, видоизменить фигуру), видят и называют получившиеся геометрические

фигуры (квадраты, треугольники, прямоугольники и др.), понимают значение слова

общая по отношению к стороне, смежная для двух фигур и т. д.

На втором этапе задания усложняются. Используются те решения, для которых

нужно изменить положение палочек, убрав или переложив их. И цель здесь другая:

учить детей рациональному способу решения задач (преобразованию). Необходимо

проанализировать задачу, высказать предположение, прежде чем действовать практически.

1. В фигуре, состоящей из 6 квадратов, убрать 2 палочки, чтобы осталось 4

квадрата.

2. Убрать 4 палочки, чтобы получился прямоугольник.

3. Убрать 3 палочки, чтобы осталось 3 квадрата.

4. В фигуре, состоящей из 5 квадратов, убрать 4 палочки, чтобы осталось 2 не-

равных квадрата.

Третий этап обучения направлен на то, чтобы постепенно подводить детей к

решению задач в уме, направлен на развитие творческой мыслительной деятельности. Даются задания на более сложное преобразование путем перекладывания пало-

чек.

1. В фигуре, состоящей из 4 квадратов, переложить 2 палочки, чтобы квадратов

стало 5.

2. В фигуре, похожей на ключ, переложить 4 палочки, чтобы получилось 3

одинаковых квадрата.

Игра с палочками развивает у детей самостоятельность мышления, творческую

12

инициативу, что необходимо для успешного овладения учебным материалом в школе.

"Задачи на составление заданной фигуры из определенного количества палочек".

Задачи на изменение фигур, для решения которых надо убрать указанное количество палочек.

"Дана фигура из 6 квадратов. Надо убрать 2 палочки так, чтобы осталось 4 квадрата".

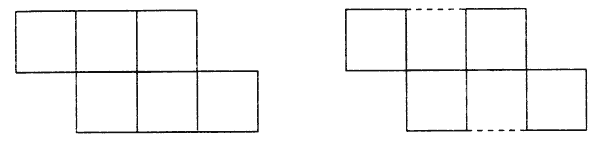
"Дана фигура, похожая на стрелу. Надо переложить 4 палочки так, чтобы получилось 4 треугольника".

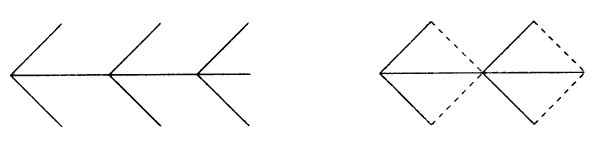
"Составить два равных квадрата из 7 палочек".

Задачи, решение которых состоит в перекладывании палочек с целью видоизменения фигуры.

"В фигуре переложить 3 палочки так, чтобы получилось 4 равных треугольника".

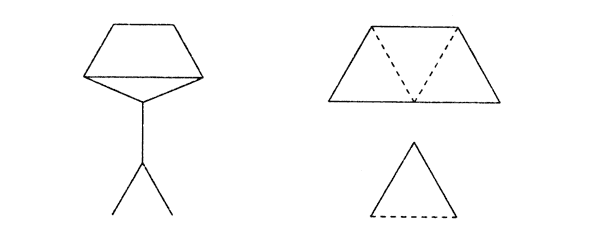
"В фигуре, состоящей из 4 квадратов, переложить 3 палочки так, чтобы получилось 3 таких же квадрата".

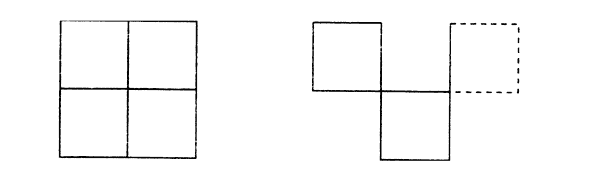
"Составить домик из 6 палочек, а затем переложить 2 палочки так, чтобы, получился флажок".

13

"Переложить 6 палочек так, чтобы, из корабля получился танк".

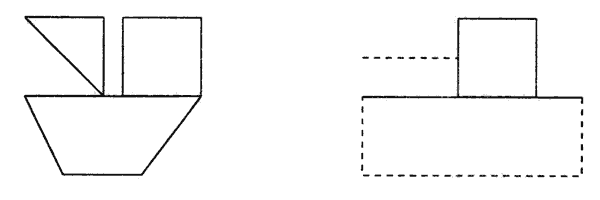
"Переложить 2 палочки так, чтобы фигура, похожая на корову, смотрела в другую сторону".

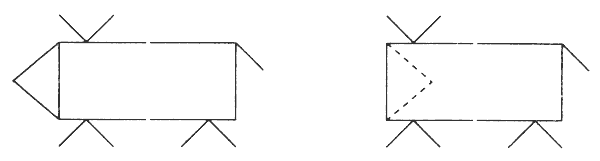
"Какое наименьшее количество палочек нужно переложить, чтобы убрать мусор из совочка?"

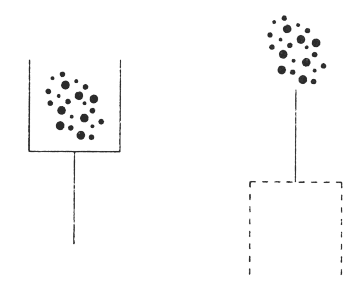
Можно использовать игры на составление фигур-силуэтов, геометрических фигур из специальных наборов, полученных при разрезании по определенным правилам какой-либо геометрической фигуры. Например, квадрат в игре «Танграм», головоломка «Пифагор», прямоугольник в играх «Пентамино», «Стомахион», «Сфинкс», овал в игре «Колумбово яйцо», круг в играх «Волшебный круг», «Вьетнамская игра» и т.д.

Эти игры направлены на уточнение знаний о геометрических фигурах и их

свойствах, на развитие сенсорных и мыслительных способностей, на усвоение способов преобразования, соединения. Они предназначены для развития у детей пространственного воображения, логического и интуитивного мышления.

Упражнения, направленные на развитие наглядно-образного мышления.

Упражнение №1. "Продолжи узор".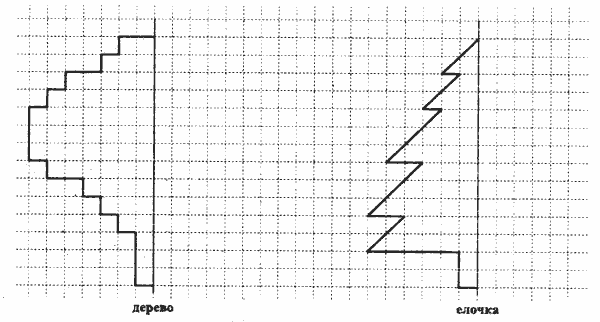

Упражнение состоит из задания на воспроизведение рисунка относительно симметричной оси. Трудность в выполнении часто заключается в неумении ребенка проанализировать образец (левую сторону) и осознать, что вторая его часть должна иметь зеркальное отображение. Поэтому, если ребенок затрудняется, на первых этапах можно использовать зеркало (приложить его к оси и посмотреть, какой же должна быть правая сторона).

14

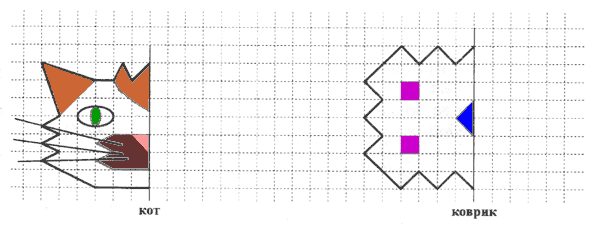
После того, как подобные задания уже не вызывают сложностей при воспроизведении, упражнение усложняется введением абстрактных узоров и цветовых обозначений. Инструкция остается такой же:

"Художник нарисовал часть картинки, а вторую половину не успел. Закончи рисунок за него. Помни, что вторая половина должна быть точно такой же, как и первая".

Упражнение №2 "Платочек".

Это упражнение сходно с предыдущим, но является более сложным его вариантом, т.к. предполагает воспроизведение узора относительно двух осей - вертикальной и горизонтальной.

"Посмотри внимательно на рисунок. Здесь изображен сложенный пополам (если одна ось симметрии) или вчетверо (если две оси симметрии) платочек. Как ты думаешь, если платочек развернуть, какой у него вид? Дорисуй платочек так, чтобы он выглядел развернутым".

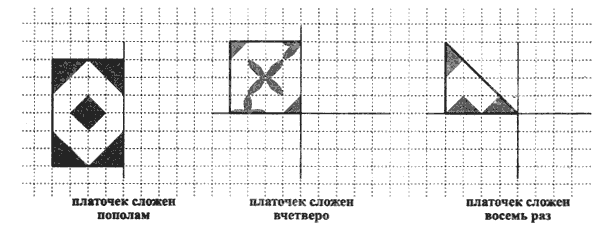
Узоры и варианты заданий можно придумать самостоятельно.

Упражнение №3. "Составь фигуру".

Это упражнение, так же, как и предыдущее, направлено на развитие образного мышления, геометрических представлений, конструктивных пространственных способностей практического плана.

Можно предложить несколько вариантов этого упражнения (от самого легкого до более сложного).

а) На каждой полоске отметь крестиком (х) две такие части, из которых можно составить круг.

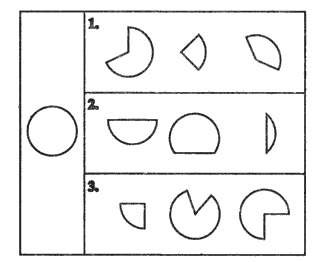
б) На каждой полоске отметь крестиком (х) две такие детали, из которых можно составить целую данную фигуру.

15

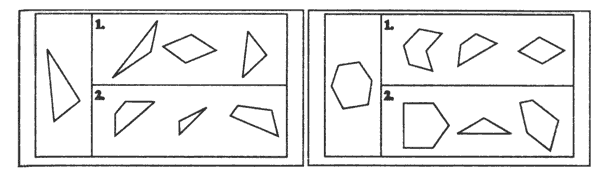
Подобного вида задания можно разработать для любых фигур - треугольников, прямоугольников, шестигранников и т.д.

Упражнение № 4. "Найди закономерность".

а) Упражнение направлено на формирование умения понимать и устанавливать закономерности в линейном ряду.

Инструкция: "Внимательно рассмотри картинки и заполни пустую клетку, не нарушая закономерности".

б) Второй вариант задания направлен на формирование умения устанавливать закономерности в таблице.

Инструкция: "Рассмотри снежинки. Нарисуй недостающие так, чтобы в каждом ряду были представлены все виды снежинок".

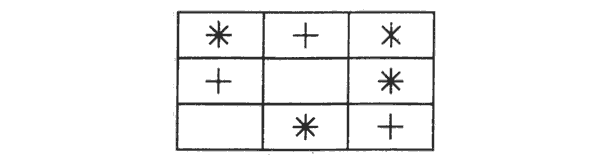
Подобные задания можно придумать самостоятельно.

Упражнение № 5. "Светофор".

"Нарисуй в клеточках красные, желтые и зеленые кружки так, чтобы в каждой строке и в каждом столбце не было одинаковых кружков".

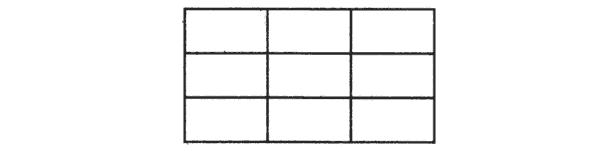
Упражнение № 6. "Классификация".

Так же, как и предыдущее упражнение, это направлено на формирование умения классифицировать по определенному признаку. Отличие заключается в том, что при выполнении этого задания правило не дается. Ребенку необходимо самостоятельно выбрать, каким образом можно разделить предлагаемые фигуры на группы.

Инструкция: "Перед тобой ряд фигур (предметов). Если бы необходимо было разделить их на группы, то как это можно сделать?"

Набор фигур.

16

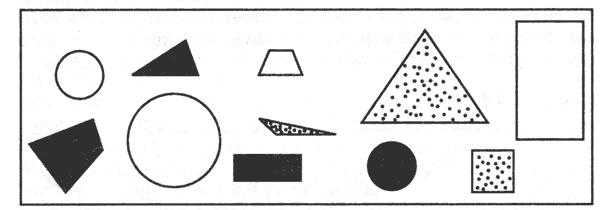
Важно, чтобы ребенок, выполняя это задание, нашел как можно больше оснований для классификации. Например, это может быть классификация по форме, цвету, размеру; деление

на 3 группы: круглые, треугольники, четырехугольники, или 2 группы: белые и не белые и т.д.

17

Методики, направленные на развитие и определение степени овладения логическими операциями мышления.

Способность выделять существенное

Учитель предлагает ряд слов: пять слов даётся в скобках, а одно – перед ними. Ученики должны за 20 секунд исключить из скобок ( то есть выделить) два слова, наиболее существенные для слова, стоящего перед скобками. Достаточно предложить из данного перечня по 5 заданий.

Сад (растение, садовник, собака, забор, земля);

Растение, земля.

Река ( берег, рыба, тина, рыболов, вода);

Берег, вода.

Куб (углы, чертёж, сторона, камень, дерево);

Углы, сторона.

Чтение (глаза, книга, картина, печать, слово);

Глаза, печать.

Игра (шахматы, игроки, штрафы, правила, наказания);

Игроки, правила.

Лес (лист, яблоня, охотник, дерево, кустарник);

Дерево, кустарник.

Город (автомобиль, здание, толпа, улица, велосипед);

Здание, улица.

Кольцо (диаметр, проба, круглость, печать, алмаз);

Диаметр, круглость.

Пение (звон, голос, искусство, мелодия, аплодисменты);

Голос, мелодия.

Больница (сад, врач, помещение, радио, больные);

Помещение, больные.

18

Любовь (розы, чувство, человек, город, природа);

Чувство, человек.

Война (аэроплан, пушки, сражения, солдаты, ружья);

Сражения, солдаты.

Спорт (медаль, оркестр, состязание, победа, стадион);

Стадион, состязание.

Обработка полученных данных: ученики, которые правильно выполнили задание, очевидно, обладают умением выделять существенное, т.е. способны к абстрагированию. Те, кто допустили ошибки, не умеют выделять существенные и несущественные признаки.

Способность к абстрагированию = число правильных ответов: 5 заданий.

Сравнение

Особую роль в организации продуктивной деятельности младших школьников в процессе обучения играет приём сравнения. Формирование умения пользоваться этим приёмом следует осуществлять поэтапно, в тесной связи с изучением конкретного содержания. Целесообразно, например, ориентироваться на такие этапы:

-выделение признаков или свойств одного объекта;

- установление сходства и различия между признаками двух объектов;

-выявление сходства между признаками трёх, четырёх и более объектов.

Так как работу по формированию у детей логического приёма сравнения лучше начать с первых уроков, то в качестве объектов можно использовать предметы или рисунки с изображением предметов, хорошо знакомых, в которых они могут выделить те или иные признаки, опираясь на имеющиеся у них представления,

(например, на уроках математики).

Для организации деятельности учащихся, направленной на выделение признаков того или иного объекта, можно сначала предложить такой вопрос:

-Что вы можете рассказать о предмете? (яблоко круглое, большое, красное; тыква – жёлтая, большая, с полосками, с хвостиком; круг – большой, зелёный; квадрат – маленький, жёлтый).

В процессе работы учитель знакомит детей с понятиями "размер", "форма" и предлагает им следующие вопросы:

19

- Что вы можете сказать о размерах (формах) этих предметов? (Большой, маленький, круглый, как треугольник, как квадрат и т.д) Цель: установить уровень развития у учащихся умения сравнивать предметы, понятия.

Учащимся предъявляются или называются какие-либо два предмета либо понятия, например:

Книга – тетрадь солнце – луна

Лошадь – корова сани - телега

Озеро – река дождь - снег

Линейка – треугольник автобус – троллейбус

Каждый ученик на листе бумаги должен написать слева черты сходства, а справа – черты различия названных предметов, понятий.

На выполнение задания по одной паре слов даётся 4 минуты. После этого листы собираются.

Обобщение

Выделение существенных признаков объектов, их свойств и отношений – основная характеристика такого приёма умственных действий, как обобщение.

Следует различать результат и процесс обобщения. Результат фиксируется в понятиях, суждениях, правилах. Процесс же обобщения может быть организован по-разному. В зависимости от этого говорят о двух типах обобщения – теоретическом и эмпирическом.

В курсе начальной математики наиболее часто применяется эмпирический тип, при котором обобщение знания является результатом индуктивных рассуждений (умозаключений).

Предлагается два слова. Учащемуся нужно определить, что между ними общего:

Дождь – град жидкость - газ

Нос – глаз предательство-трусость

Сумма – произведение водохранилище - канал

Сказка – былина школа - учитель

История – природоведение доброта – справедливость

Можно предложить 5 пар слов. Время 3-4 минуты. Обработка полученных данных:

Уровень умения общаться = число правильных ответов: 5 заданий.

20

Классификация

Умение выделять признаки предметов и устанавливать между ними сходство и различие – основа приёма классификации. Умение выполнять классификацию формируется у школьников в тесной связи с изучением конкретного содержания.

Эта методика также выявляет умение обобщать, строить обобщение на отвлечённом материале.

Инструкция: даны пять слов. Четыре из них объединены общим признаком. Пятое слово к ним не подходит. Необходимо найти это слово.

1) Приставка, предлог, суффикс, окончание, корень.

2) Треугольник, отрезок, длина, квадрат, круг.

3) Дождь, снег, осадки, иней, град.

4) Сложение, умножение, деление, слагаемое, вычитание.

5) Дуб, дерево, ольха, тополь, ясень.

6) Василий, Фёдор, Иван, Петров, Семён.

7) Молоко, сыр, сметана, мясо, простокваша.

8) Секунда, час, год, вечер, неделя.

9) Горький, горячий, кислый, солёный, сладкий.

10) Футбол, волейбол, хоккей, плавание, баскетбол.

11) Тёмный, светлый, голубой, яркий, тусклый.

12) Самолёт, пароход, техника, поезд, дирижабль.

13) Круг, квадрат, треугольник, трапеция, прямоугольник.

14) Смелый, храбрый, решительный, злой, отважный.

Учащимся можно предложить 5 заданий. Время – 3 минуты.

Обработка полученных данных:

Уровень сформированности мыслительной операции = число правильных ответов: 5 заданий.

21

Анаграмма

Цель: выявить наличие или отсутствие у школьников теоретического анализа.

Ход работы: учащимся предлагаются анаграммы (слова, преобразованные путём перестановки входящих в них букв).

Учащиеся должны по данным анаграммам найти исходные слова.

ЛБКО, РАЯИ, ЕРАВШН, РКДЕТИ, АШНРРИ, УПКС, ОКОРАВ

Школьники в результате выполнения задания могут разделиться на 2 группы: 1 группа – у них отсутствует теоретический анализ (способность мысленно выделять свойства предметов, в данном случае – структуру слова), 2 группа учащихся быстро находит ответы, обнаружив общее правило.

Обработка полученных данных: уровень сформированности операций = число правильных ответов: 5 заданий.

Анализ отношений понятий (аналогия)

Понятие "аналогичный" в переводе с греческого языка означает "сходный", "соответственный", понятие аналогия – сходство в каком-либо отношении между предметами, явлениями, понятиями, способами действий.

Формируя у младших школьников умения выполнять умозаключения по аналогии, необходимо иметь ввиду следующее:

-Аналогия основывается на сравнении, поэтому успех её применения зависит от того, насколько ученики умеют выделять признаки объектов и устанавливать сходство и различие между ними.

-Для использования аналогии необходимо иметь два объекта, один из которых известен, второй сравнивается с ним по каким-либо признакам. Отсюда, применение приёма аналогии способствует повторению изученного и систематизации знаний и умений.

-Для ориентации школьников на использование аналогии необходимо в доступной форме разъяснить им суть этого приёма, обратив их внимание на то, что в математике нередко новый способ действий можно открыть по догадке, вспомнив и проанализировав известный способ действий и данное новое задание.

-Для правильных действий по аналогии сравниваются признаки объектов, существенные в данной ситуации. В противном случае вывод может быть неверным.

Например, даны три слова, первые два находятся в определённой связи. Между третьим и одним из предложенных пяти слов существуют такие же отношения. Надо найти это четвёртое слово:

Песня: композитор = самолёт:?

22

а) аэродром; б) горючее; в) конструктор г) лётчик; д) истребитель.

Функциональные отношения: песню сочинил композитор.

Ответ – конструктор (конструктор сделал самолёт).

Задания:

1) школа: обучение = больница:?

а) доктор; б) ученик; в) лечение; г) учреждение; д) больной.

2) песня: глухой = картина:?

а) слепой; б) художник; в) рисунок; г) больной; д) хромой.

3) нож: сталь = стол:?

а) вилка; б) дерево; в) стул; г) столовый; д) длинный.

4) паровоз: вагоны = конь:?

а) поезд; б) лошадь; в) овёс; г) телега; д) конюшня.

5) лес: деревья = библиотека:?

а) город; б) здание; в) книги; г) библиотекарь; д) театр.

6) бежать: стоять = кричать 6?

а) ползать; б) молчать; в) шуметь; г) звать; д) плакать.

7) утро: ночь = зима:?

а) мороз; б) день; в) январь; г) осень; д) сани.

8) волк: пасть = птица:?

а) воздух; б)клюв; в) соловей; г) яйцо; д) пение.

9) холодно: горячо = движение:?

а) покой; б) взаимодействие; в) инерция; г) молекула; д) бежать.

10) слагаемое: сумма = множители:?

а) разность; б) делитель; в) произведение; г) умножение; д) деление.

11) круг: окружность = шар:?

23

а) пространство; б) сфера; в) радиус; г) диаметр; д) половина.

12) светло: темно = притяжение:?

а) металл; б) магнит; в) отталкивание; г) движение; д) взаимодействие.

Эта методика позволяет выявить у учащихся умение определять отношения между понятиями или связи между понятиями:

а) причина – следствие; г) часть – целое;

б) род – вид; д) функциональные отношения.

в) противоположность;

Уровень сформированности операций = число правильных ответов: число заданий.

Для изучения скорости протекания мыслительных процессов учащихся можно использовать метод, суть которого состоит в заполнении пропущенных букв в предложенных словах.

П – РО З – Р – О З – О - ОК

К – СА Д – Р – ВО Т – А - А

Р – КА К –М – НЬ К – Н - А

Г – РА Х – Л – Д К – Ы - А

П -ЛЕ К – В – Р П – Е – А

Учитель обращает внимание на то, сколько потребовалось школьнику времени на обдумывание каждого отдельного слова и заполнение пропущенных букв.

Варианты заданий на развитие логического мышления младших школьников

Предлагаемые методики были апробированы. На выполнение заданий потребуется 45 минут. Учащимся раздаются задания по вариантам (на исследование мышления). На выполнение 1 – 5-го заданий необходимо дать 5 минут; 6-го - 15 минут.

Вариант 1

Задание 1. В приведённых словах буквы переставлены местами. Запишите эти слова.

1) лбко; 2) раяи; 3) еравшн; 4) ркдети; 5) рбкадоле.

Задание 2. Перед скобками слово, а в скобках – ещё 5 слов. Найдите 2 слова из написанных в скобках, которые наиболее существенны для слова, стоящего перед скобками. Запишите эти слова.

24

1) Чтение ( книга, очки, глаза, буква, луна).

2) Сад (растение, садовник, земля, вода, забор).

3) Река (берег, тина, вода, рыболов, рыба).

4) Игра (шахматы, игроки, правила, футбол, штраф).

5) Куб (углы, дерево, камень, чертёж, сторона).

Задание 3. Сравните понятия: книга – тетрадь. Общие и отличительные черты выпишите на листе в 2 столбика.

Задание 4. Какое понятие в каждом из перечней является лишним? Выпишите его.

1) Дуб, дерево, ольха, ясень.

2) Горький, горячий, кислый, солёный, сладкий.

3) Дождь, снег, осадки, иней, град.

4) Запятая, точка, двоеточие, союз, тире.

5) Сложение, умножение, деление, слагаемое, вычитание.

Задание 5. Вам предлагается 5 пар слов. Надо определить, что между ними общего (очень коротко, предложение должно содержать не более 3 – 4 слов).

1) Дождь – град.

2) Нос – глаз.

3) Сумма – произведение.

4) Водохранилище – канал.

5) Предательство – трусость.

Задание 6. Даны 3 слова. Два первых находятся в определённой связи. Третье и одно из пяти слов, приведённых ниже, находятся в такой же связи. Найдите и запишите на листе это четвёртое слово.

1) волк: пасть = птица:?

а) воробей; б) гнездо; в) клюв; г) соловей; д) петь.

2) библиотека: книга = лес:?

а) берёза; б) дерево; в) ветка; г) бревно; д) клён.

25

3) птица: гнездо = человек:?

а) люди; б) рабочий; в) птенец; г) дом; д) разумный.

4) слагаемое: сумма = множители:?

а) разность; б) делитель; в) произведение; г) умножение; д) вычитание.

5) холодно: горячо = движение:?

а) взаимодействие; б) покой; в) мяч; г) трамваи; д) идти.

6) запад: восток = обмеление:?

а) засуха; б) юг; в) наводнение; г) река; д) дождь.

7) война: смерть = тепло:?

а) дыхание; б) жизнедеятельность; в) вещество; г) температура; д) гибель.

8) молния: свет = жара:?

а) солнце; б) трава; в) жажда; г) дождь; д) река.

9) роза: цветок = газ:?

а) кислород; б) дыхание; в) горение; г) состояние вещества; д) прозрачный.

10) берёза: дерево = стихотворение:?

а) сказка; б) богатырь; в) поэзия; г) лирика; д) драма.

Вариант 2

Задание 1. В приведённых словах буквы переставлены местами. Запишите эти слова.

1) УПКС; 2) АШНРРИ; 3) ВЦТЕКО; 4) ОКАМНДРИ; 5) ЛКБУИНАК.

Задание 2. Перед скобками слово, а в скобках – ещё 5 слов. Найдите 2 из них, которые являются наиболее существенными для слова, стоящего перед скобками.

1) деление (класс, делимое, карандаш, делитель, бумага).

2) Озеро (берег, рыба, вода, рыболов, тина).

3) Огород (забор, земля, растение, собака, лопата).

4) Чтение (глаза, очки, книга, печать, картинка).

5) Игра (шахматы, теннис, игроки, штраф, правила).

26

Задание 3. Сравните понятия: озеро – река. Общие и отличительные черты выпишите в 2 столбика.

Задание 4. Какое понятие в каждом из перечней является лишним? Выпишите его.

1) Холодный, горячий, тёплый, кислый, ледяной.

2) Роза, тюльпан, нарцисс, цветок, гладиолус.

3) Справедливость, доброта, искренность, зависть, честность.

4) Треугольник, отрезок, квадрат, круг, прямоугольник.

5) Пословица, поговорка, басня, сказка, былина.

Задание 5. Предлагается 5 пар слов. Надо определить, что между ними общего (очень коротко, фраза должна содержать до 3-х слов).

1) Русский язык – математика.

2) Нос – глаз.

3) Землетрясение – смерч.

4) Газ – жидкость. Зависть – трусость.

Задание 6. Даны 3 слова. Два первых находятся в определённой связи. Третье и одно из 4 приведённых ниже находятся в такой же связи. Найдите и запишите четвёртое слово.

1) Песня: композитор = самолёт:?

а) горючее; б) лётчик; в) конструктор; г) аэродром.

2) прямоугольник: плоскость = куб:?

а) пространство; б) ребро; в) высота; г) треугольник.

3) школа: обучение = больница:?

а) доктор; б) больной; в) лечение; г) учреждение.

4) ухо: слышать = зубы:?

а) видеть; б) лечить; в) жевать; г) рот.

5) глагол: спрятать – существительное:?

а) понятие; б) склонять; в) название; г) образовывать.

6) светло: темно = притяжение:?

27

а) металл; б) молекула; в) отталкивание; г) движение.

7) жара: засуха = дожди:?

а) паводок; б) наводнение; в) осень; г) лето.

8) берёза: дерево = стихотворение:?

а) сказка; б) лирика; в) поэзия; г) драма.

9) роза: цветок = кислород:?

а) состояние вещества; б) газ; в) предмет; г) гвоздика.

10) север: юг = ночь:?

а) утро; б) светло; в) день; г) вечер.

Методика оценки

Тесты	Высокий уровень	Выше среднего	Средний уровень	Ниже среднего	низкий
1. Анаграмма.	5	4	3	2	1
2. Существенное.	5	4	3	2	1
3. Сравнение.	5	4	3	2	1
4. Классификация	5	4	3	2	1
5. Обобщение.	5	4	3	2	1
6. Аналогия.	9 - 10	7 - 8	5 - 6	3 - 4	0 - 2
За каждый правильный ответ присваивается 1 балл.
Общий уровень развития мышления	30 - 35	24 - 29	18 - 23	10 - 17	0 - 9

Предложенные задания, упражнения, игры позволят преподавателям начальной школы и родителям подготовить учащихся к обучению в среднем звене.

Диагностические методики будут необходимы для того, чтобы выявить слабые стороны, те мыслительные операции, которые в недостаточной степени сформированы, но которые могут быть развиты при проведении целенаправленных занятий с детьми, а также при обучении в среднем звене.

28

Приложение

ЗАДАЧИ, РАЗВИВАЮЩИЕ ЛОГИЧЕСКОЕ МЫШЛЕНИЕ.

1. КЛАСС.

1. У Оли было орехов больше 3, но меньше 7. Сколько орехов было у Оли? (4,5,6)

2. Бабушка дала Серёже журнал «Ералаш» со 2 номера по 8.Сколько журналов у него?(7)

3. Расставить 6 книг на две полки так, чтобы на одной было на 2 книги больше, чем на дру-

гой. (4 и 2)

4. В люстре 5 лампочек. Через некоторое время 3 лампочки перегорели. Сколько лампочек придется заменить?

5. У Толи 2 пары варежек. Сколько варежек на правую руку? (2)

6. В семье 4 детей. Сестер столько же, сколько и братьев. Сколько девочек в семье? (2)

7. В корзине сидят котята. У всех котят три пары ушей. Сколько котят в корзине? (3)

8. У паука 4 пары ног. Сколько всего ног у паука? (8)

9. Дима выиграл у Алеши 3 партии в шахматы. Алеша проиграл Диме столько же партий и одну партию мальчики сыграли вничью. Сколько всего партий сыграли дети? (4)

10. Сколько целых батонов хлеба можно составить из 6 половинок? (3)

11. По дороге друг за другом идут 5 детей. За каждым мальчиком, кроме последнего, идет

девочка. Сколько девочек идет по дороге? (2)

12. Я задумала два числа. Когда сложила их, то получила 6, когда вычла одно из другого, то тоже получила 6. Какое число я задумала? (6 и 0)

13. В семье двое детей. Саша – брат Жени, но Женя Саше не брат. Может ли такое быть? Кто Женя? (сестра).

1. Поезд состоит из 10 вагонов. Петя сел в пятый вагон от начала поезда, а Дима в пятый вагон от конца поезда. В одном ли вагоне едут мальчики? (нет).

29

15. Плитка шоколада состоит из 6 квадратных долек. Сколько разломов нужно сделать, чтобы разломить эту плитку на отдельные дольки? ( 5 ) .

1. Пётр – сын Сергея, Сергей – сын Фёдора. Кем приходится Пётр Фёдору? (внук).

2. Из книги выпало несколько листов. На первой странице стоит № 5, на последней

№ 10. Сколько листов выпало из книги? (3 листа).

1. Меня зовут Иваном Сергеевичем, а моего деда - Петр Николаевич. Как зовут моего отца? (Сергей Петрович).

2. Мама купила детям три пары варежек, Сколько варежек на одну руку? (3).

3. В парке было 7 скамеек. 3 скамейки заменили новыми. Сколько скамеек в парке?

4. На уроке физкультуры учитель попросил 10 учеников рассчитаться слева направо по порядку. Юра оказался третьим. Каким по счету будет Юра, если расчет пойдет справа налево? (8).

5. У всех цыплят, сидящих в корзине, Юля насчитала 10 ног. Сколько было цыплят в корзине? (5)

6. Наташа сказала, что у неё кукол больше 5, но меньше 8. Сколько кукол у Наташи?

7. Коля старше Сережи, Сережа старше Миши. Назови имя самого маленького мальчика. (Миша)

8. Кролики сидят в клетке так, что видны только их уши. Коля насчитал 5 пар ушей. Сколько кроликов в клетке?

9. Кузнец подковал двух лошадей. Сколько подков ему понадобилось?

10. В слове «кошка» 5 букв. Придумай слово в котором букв на одну меньше и оно обозначает животного (тигр).

11. В слове «кот» и в слове « мяу» по три буквы. Одинаковое ли количество слогов в словах?

12. Роме подарили столько значков, сколько у него было. Рома пересчитал значки и их оказалось 8. Сколько значков было у мальчика? (4)

13. Чтобы рассадить 7 детей не хватает два стула. Сколько стульев в комнате? (5)

14. У паука 4 пары ног, а у жука 3 пары ног. На сколько ног меньше у жука? (на одну пару т.е. 2 ноги).

15. Сестра старше брата на один год. На сколько сестра лет сестра будет старше брата через 5 лет ? (на один год) .

30

1. В ящике стола лежат деньги, на которые можно купить два одинаковых стула и одно кресло. Что дороже кресло или стул? (кресло)

2. Купили пакет кефира. Половину пакета выпили Никита и Даша. В пакете осталось 2 стакана. Сколько стаканов кефира было в пакете? (4)

3. Разность двух чисел равна вычитаемому. Приведите пример такого выражения. ( таких выражений мн-во 6-3=3, 14 – 7=7 ит.д. )

4. Бабушка положила на тарелку 12 груш. После того, как внуки взяли по одной груше, осталось 8 груш. Сколько внуков у бабушки? (4).

5. Каждой из трёх внучек дедушка разрешил сорвать с 4 кустов по одной розе. Сколько роз сорвали девочки? (4+4+4=12 роз)

1. КЛАСС.

1. На веревке завязали 4 узла так, что концы веревки остались свободными. На сколько частей разделилась веревка? (на 5)

2. В коробке умещается 10 красных и 6 синих бусинок. Какие бусинки мельче: красные или синие? (красные)

3. В парке 4 зеленых и коричневые скамейки. Зеленых скамеек больше. Сколько скамеек каждого цвета? (3 зеленые и 1 коричневая)

4. Петя и Паша живут в девятиэтажном доме. Петя живет выше Паши. Паша живет в квартире на 7 этаже. На каком этаже живет Петя? (на 8 или 9)

5. Колесо велосипеда имеет 8 спиц. Сколько промежутков между спицами? (8)

6. Купили щуку, леща и окуня. Щука тяжелее леща, а лещ тяжелее окуня. Какая рыба самая лёгкая? (окунь)

7. В большой клетке 6 волнистых попугайчиков, а в маленькой - 5. Из большой клетки в маленькую пересадили 1 попугайчика. Поровну ли попугайчиков в клетках? ( нет )

8. На этой неделе в гостях у бабушки Галя была в среду, четверг, пятницу, а Лариса - в четверг, субботу, пятницу, воскресенье. Сколько дней гостила у бабушки хотя бы одна внучка? («Хотя бы одна» значит либо Галя, либо Лариса, либо обе вместе одновременно. Значит среда, четверг, пятница, суббота, воскресенье.)

9. В корзине и пакете по 6 апельсинов. Из пакета переложили в корзину один апельсин. На сколько апельсинов меньше стало в пакете? (на 2)

31

1. У меня три фото. На двух я и на двух мама. Может ли это быть? (да, на одной из фото я вместе с мамой)

2. Масса двух одинаковых пирогов такая же как и одного торта. Масса пирога - 1 килограмм. Какова масса торта? (2 КГ)

3. Половину всех своих золотых монет Буратино отдал в харчевне, а остальные по совету кот Базилио и лисы Алисы закопал на поле чудес. Сколько монет было у Буратино? (6)

4. У брата было 5 орехов. Один орех он отдал сестре, у которой уже были орехи, и орехов у них стало поровну. Сколько орехов было у сестры? (6)

5. Папа Карло заготовил 13 ножек для стульев. Хватит ли этих ножнк для того, чтобы изготовить стульчики для Пьеро, Мальвины, Буратино? (4+4+4=12 12 меньше 13 значит хватит ножек)

6. У Веры 9 конфет, а у Оли 5 конфет. Сколько конфет Вера должна отдать Ольге, чтобы конфет стало поровну? (2)

7. На одной чашке весов лежит арбуз и гиря в 3 кг. На другой - две гири по 5 кг. Найди массу арбуза. (7 кг)

8. К празднику мама приготовила Маше. Нине, Оле подарки: мишку, куклу и собачку. Какой подарок получила каждая девочка, если Маша выбрала себе не куклу и не собачку, а Оля тоже не взяла куклу? ( Маша - мишка, Нина- кукла, Оля-собачка )

9. Термометр показывает 12* мороза. Через некоторое время столбик ртути в термометре опустился на 3* . Теплее стало или холоднее и на сколько градусов ? ( холоднее на 3* )

10. Может ли сумма двух чисел быть равной их разности? (несколько вариантов решения например 3+0=3 и 3-0=3)

11. В вазе на 20 конфет больше, чем в двух одинаковых пакетиках. В вазе 30 штук. Сколько конфет в пакетике? (30-20=10:2=5 конфет)

12. На столе стоят матрешки. В каждой из 3 больших умещается по 5 маленьких матрешек. Сколько матрешек на столе? (15+3=18 или если в каждом комплекте 1 большая + 5 маленьких=6 штук, а комплектов три, значит матрешек 18)

13. Каждую головку сыра продавец разрезал пополам. Сколько головок сыра было, если получилось 6 половинок? (3 головки)

32

1. В пакете столько же лимонов сколько и в корзине. Из пакета взяли 3 лимона, а из корзины взяли 5 лимонов. Где осталось лимонов больше и на сколько? (на 2 в пакете)

2. В двух ваза поровну конфет. Когда из одной взяли 5, а в другую положили 5, то в обеих вазах конфет стало 20. Сколько конфет было в каждой вазе сначала? (по 10 конфет)

3. Петя полил в саду столько же яблонь, сколько и Оля. Когда Петя полил еще и грушу, то оказалось он полил 9 деревьев. Сколько яблонь полил Петя? (9-1=8:2=4)

4. Чтобы рассадить всех детей в зале не хватает 6 стульев. Когда принесли несколько стульев, то 2 стула оказались лишними. Сколько стульев принесли в зал? (6+2=8)

5. У брата столько же игрушек сколько у сестры. Когда брату подарили 4 игрушки, то у него стало 12 игрушек. Сколько игрушек было у сестры? (12-4=8 игрушек)

6. Сколько двухцветных полосок можно сделать из 3 полосок: красной, синей, зеленой? (3 штуки кр.-син, кр.-зел, син.-зел.)

7. Запиши цифрами все двузначные числа, которые можно составить используя слова «двадцать», « сорок», «один», «пять», «семь». (20,21,25,27,40,41,45,47)

8. Через верхний край в бак за час наливается 12 ведер воды, а через нижний кран выливается 8 ведер. Оба крана открыли одновременно. Сколько ведер воды нальется в бак, если он был открыт 2 часа? (12-8=4х2=8 ведер)

9. Валя, Галя и Даша одеты в платья трех цветов: красное, голубое, жёлтое. Какого цвета платья на каждой девочке, если Валя не в красном и не в голубом, а Галя не в красном? (Валя - желтое, Галя - голубое, Даша - красное)

10. В шкафу стояли 3 мелких и 4 глубоких тарелки. Из шкафа взяли 4 тарелки. Сколько и каких тарелок могли взять? (3м.+1г; 2м+2г; 1м+3г; 4глубоких)

11. Если каждый из трех мальчиков возьмёт из вазы по 4 абрикоса, в вазе останется 1 абрикос. Сколько было абрикосов? (4х3=12+1=13)

12. Хватит ли 8 парт, чтобы рассадить 20 учеников? (8х2=16 это меньше 20, значит не хватит)

13. Трое друзей играли в шахматы, каждый сыграл 2 партии. Сколько всего партий было сыграно? (3 партии)

14. Врач назначил Мите лекарство по 3 таблетки в день в течении недели. Хватит ли стандарт из 50 таблеток. (3х7=21 значит таблеток хватит)

15. Шнур 12 м. разрезали на 3 части. Сколько надрезов сделали? (3-1=2 надреза)

33

1. В корзине на 8 помидоров больше, чем в пакете. Сколько помидоров нужно переложить в пакет, чтобы помидоров стало поровну? (3 помидора)

2. У Наташи и Оли поровну леденцов. Когда Наташа съела 2 леденца, то вместе у обеих девочек стало 10 леденцов. Сколько леденцов было у каждой из них? (10+2:2=6 леденцов было у каждой)

3. Трое ребят катались на двухколесных и трехколесных велосипедах. У всех велосипедов было 7 колес. Каких велосипедов было и сколько? (способом подбора 7=2+2+3 , значит 2 – двухколесных и 1 - трехколесный)

4. Гвоздь длиной 8 см., забили в доску так, что с одной стороны он выступает на 2см. а с другой на 1 см. Найди толщину доски. (8-1-2=5 см)

5. Может ли сумма двух чисел равняться их произведению? (2+2=2х2)

6. Чему равно произведение 0 х 1 х 2 х 3 х 4 =? Почему, объясни.

7. Лестница имеет 15 ступенек. На какую ступеньку надо подняться, чтобы оказаться точно посередине лестницы? (на 8 - ю)

8. На одной чашке лежит арбуз, на другой 6 апельсинов. Весы в равновесии. Во сколько раз апельсин легче арбуза? (в 6 раз)

9. На листе написано число, которое не больше 10, но и не меньше. Какое это число ? ( это число 10 )

10. В классе 31 ученик. Сколько нужно парт, чтобы рассадить всех учащихся ? ( 16 )

11. В коробке 5 белых кубиков и 3 чёрных. Какое наименьшее число кубиков надо взять, чтобы из них был хотя бы 1 чёрный ? ( 6 кубиков )

12. Сегодня в 12 часов дня в Москве идет дождь. Можно ли ожидать через 14 часов солнечную погоду? Объясни (нет, т.к. в это время будет 2 часа ночи)

13. В записи « 6 5 2 » расставьте знаки действий и скобки, чтобы значение выражения было равно 42. ((6 х (5 + 2) = 42)

14. Для каждого детского велосипеда нужно 1 большое колесо и 2 маленьких колеса. Сколько получится детских велосипедов, имея 12 маленьких колес и 7 больших колес? (6 велосипедов и останется 1 большое колесо)

15. На верхней полке 3 книги, на нижней - 2. Сколько книг надо поставить ещё на нижнюю полку, чтобы книг стало в 2 раза больше, чем на верхней полке? (на нижней полке должно быть 6 книг, но там уже есть 2 книги. Значит 6 - 2 = 4 надо 4 книги)

16. Запиши с помощью 1 0 все трехзначные числа. (100, 101, 110, 111.)

34

1. КЛАСС.

1. Трое друзей поехали на дачу. Дорога заняла 6 часов. Сколько часов ехал каждый? (6 часов)

2. На дереве сидели 3 галки и 2 вороны.2 птицы улетели. Сколько и какие птицы могли остаться? (3 галки, 1 ворона и 2 галки, 2 вороны и 1 галка)

3. Внашем доме живут Катя, Маша и Лена. Вчера я видела Катю и Машу. Одной из них 9 лет, другой - 8 лет. Сегодня я видела Машу и Лену. Одной из них 10 лет, другой - 9 лет. Кому сколько лет? (М – 8, К – 8, Л – 10)

4. При встречи три товарища пожали друг другу руки. Подсчитай число рукопожатий. (3 рукопожатия)

5. На аллее в парке через каждые 4 метра посажены рябины. Кроме этого по одной рябине посажено в начале аллее и в конце. Длина аллеи 32 метра. Сколько рябин на аллее? (10 штук)

6. На блюдце разложили 18 штук вафлей так: 4, 5, 2, 7. Как можно не трогая вафли на 2 стола так, чтобы на одном было в 2 раза больше, чем на другом? (первый стол 5 и 7, второй стол 4 и 2)

7. Масса арбуза и ещё половина такого же арбуза равна 9 кг. Найди массу арбуза. (6 кг)

8. На тарелке лежат сливы. Марина взяла половину всех слив, а Алёша - остальные 4 сливы. Узнай сколько слив было на тарелке? (8 слив)

9. Попугай, сидя на плече у клоуна, раздает детям карточки в таком порядке: белая, синяя, зеленая, красная. Незнайка был седьмым. Какого цвета карточку он получит? (зеленую)

10. Незнайка посадил 50 горошин. Из каждого десятка не взошло 2 горошины. Сколько всего семян не взошло? (10 семян)

11. Кусок проволоки 12 см. согнули так, что получилась рамка. Какими могут быть стороны рамки? (12 : 2 = 6 значит 3 и 3, 5 и 1, 4 и 2)

12. Нина написала четырехзначное число. Вычла 1 и получила трехзначное число. Какое число написала Нина? (1000 – 1 == 999)

13. Женя решил прогуляться и пошел по левому берегу ручья. Во время прогулки он 3 раза перешел ручей. На левом или на правом берегу находится Женя? (на правом)

35

1. Ване надо встать завтра в 9 часов утра. Вечером в 6 часов он завел будильник на 9 часов и лег спать. Через какое время его разбудит будильник? (будильник зазвенит в 9 часов вечера, значит через 3 часа)

2. К трехзначному числу слева приписали единицу. На сколько увеличилось число? (на 1000)

3. Используя цифры 0, 4, 2, 7, 9, 1, запиши наибольшее и наименьшее шестизначное число. (974210 и 102479)

4. Каждый торт разрезали пополам, потом каждую половинку еще раз пополам. На каждое из 12 блюдец положили 1 кусок торта. Сколько было тортов? (12: 4 = 3 т.к. каждый торт разрезан на 4 части)

5. Число 16 запишите в виде произведения двух таких чисел, сумма которых наименьшая. ( 16 = 8 х 2 16 = 16 х 1 16 = 4 х 4

1. 8 + 2 = 10 16 + 1 = 17 4 + 4 = 8 )

1. Мотоцикл поехал 160 км. Со скоростью 80 км/ час, насколько раз останавливался в пути. Сколько времени мотоцикл затратил на весь путь, если остановка заняла 25 минут? (160 : 80 + 25 = 2 часа 25 минут)

2. В комнату 20 м. кв. и шириной 4 м. хотят положить ковер размером 3 х 2 м. Можно ли это сделать? ( Длина комнаты 20 : 4 = 5 м. значит можно )

3. Сколько получится если число 1 умножить на себя 1000 раз? Объясни почему.

4. Площадь пр-ка 12 см. кв. Какими могут быть его стороны? (12 и 1, 3 и 4, 6 и 2)

1. КЛАСС.

1. Запишите все двухзначные числа, в которых число десятков в 3 раз меньше числа единиц или больше. (13, 26, 39. или 31, 62, 93)

2. Запишите все трехзначные числа, в которых каждая следующая цифра на 1 больше предыдущей (123, 234, 345. 456. 567, 678. 789)

3. Незнайка решил искупаться. Он разделся, сложил одежды и поплыл. « Сейчас переплыву реку три раза и оденусь и пойду домой». Как вы думаете, нашел ли Незнайка свою одежду? Объясни ответ (нет т.к. три раза это значит оказаться на другом берегу)

4. К числу 5 приписать справа и слева цифру 5 .Во сколько раз увеличилось число? (в 111 раз)

36

1. Анна - дочь Марии. Мария - дочь Светланы. Кем приходится Светлана Анне? (бабушка)

2. Каждая из девочек Саша и Маша пошли в кино с мамой. Сколько человек пошли в кино? (или 3, или 4)

3. При каком значении х выражение 200 : х принимает наименьшее значение ? ( при х = 200 т.к. 200 : 200 = 1 )

4. При каком значении а выражение 500 : а принимает наибольшее значение.? ( при а = 1 т.к. 500 : 1 = 500 )

5. Покупатель купил 15 голубых конвертов и 10 с марками. На 5 голубых конвертах были марки. Сколько конвертов купил покупатель? (20 конвертов)

6. В корзине яблок меньше 10. Эти яблоки можно разделить поровну между 2 детьми или 3 детьми. Догадайся, сколько яблок в корзине? (6 яблок)

7. Кот Матроскин, Шарик, Галчонок, решили сфотографироваться и послать фото Дяде Федору. Они уселись на скамеечке возле дома. В каком порядке слева направо они могут сидеть ? ( несколько вариантов ответа : 1 – М,Ш,Г. 2 – М,Г,Ш. 3 – Ш,М,Г. 4 – Ш,Г,М. 5 – Г,Ш,М. 6 – Г,М,Ш. )

8. Доктор Пилюлькин прописал Незнайке принимать ложку лекарства через каждые 20 минут. На сколько времени хватит Незнайке этого лекарства, если в пузырьке его ровно на 3 приема? (на 40 минут)

9. Масса 4 одинаковых яблок такая же, как масса одного грейпфрута. Масса яблока и грейпфрута равна 750 г. Найди массу яблока. ( Положим на весы вместо грейпфрута 4 яблока тогда будет 5 яблок и их масса = 750 гр. Значит 750 : 5 = 150 гр. Вес одного яблока )

ЗАНИМАТЕЛЬНЫЕ ВОПРОСЫ, ЗАГАДКИ, СМЕКАЛКИ, СТАРИННЫЕ ЗАДАЧИ

1. Два числа 1 и 3 быстро их сложи и ответ скажи.

2. На дереве сидят 4 птицы:2 – воробья остальные вороны. Сколько ворон?

3. Купил на 5 рублей, уплатил 6 рублей. Сколько сдачи получил?

4. На столе было 4 яблока. Одно разрезали на 4 части. Сколько яблок на столе ?

5. Как можно одним мешком пшеницы наполнить два таких мешка? (Один вложить

в другой )

1. У бабушки Маши внучка Даша, кот Пушок, да собака Дружок. Сколько внуков?

37

1. Задумай число до 5. Прибавь 2 и скажи ответ. Я назову задуманное число.

2. Кто в твоей семье самый старший, низкий, выше отца, мамы, старше тебя, выше тебя, ниже тебя, ниже мамы?

3. У стены стоит кадушка, а в кадушке той лягушка. Если было б 7 кадушек сколько было бы лягушек?

4. Первый Назар шёл на базар, второй Назар – шел с базара. Какой Назар нес товар, а какой шел без товара?

5. Двое детей подошли к реке. У берега стоит одна лодка, которая берет только человека. Как им переплыть на другой берег? ( дети были на разных берегах)

6. Мальчик пришел на мельницу и увидел в каждом углу по три мешка, на каждом мешке по 3 кошки, у каждой кошки по три котенка. Сколько ног было на мельнице ? (две, потому что у кошек лапы )

7. Над рекой летали птицы: голубь, щука, две синицы, два стрижа и пять гусей. Сколько птиц ответь скорей?

8. Горело 7 свечей. 2 свечи погасли. Сколько свечей осталось?

9. Как перечислить пять дней недели, не называя их? (позавчера, вчера, сегодня, завтра, послезавтра)

10. Когда человек может мчаться со скоростью гоночного автомобиля? ( Когда сидит в нем )

11. Кто может прыгнуть выше дома? (Любой, т.к. дома не прыгают)

12. Скажешь: « Не приходи» - идет. Скажешь: « Не уходи» - уходит (время)

13. Ты да я да мы с тобой. Сколько нас? ( двое )

14. Как с помощью только одной палочки образовать треугольник на столе? (положи на угол)

15. Тройка лошадей пробежала 5 км. Сколько км пробежала каждая лошадь.

16. Если курица стоит на одной ноге, то она весит 2 кг, А если встанет на две ноги?

17. У трех братьев по одной сестре. Сколько детей в семье? (4)

18. Надо разделить 5 яблок на 5 девочек так, чтобы одно яблоко осталось в корзине и

каждой досталось по одному яблоку (последней дать яблоко вместе с корзиной)

1. Может ли дождь идти 2 дня подряд? (нет, их разделяет ночь).

38

1. Росло 4 березы на каждой по 4 больших ветки, на каждой большой ветке по 4 меленькой веточки, на каждой маленькой веточке по 4 яблока. Сколько всего яблок?

2. В огороде пугало рукавами машет. В огороде пугало разгоняет пташек.

3 паслись на грядке лука, в небеса взвилися 3.

2 последние не трусят – очень храбрые они.

28. Скоро10 Сереже, Диме нет ещё 6. Дима все никак не может до Сережи подрасти. А на сколько же моложе мальчик Дима, чем Сережа?

29. Три сестрички заплели по две косички. Угадайте, вот вопрос, сколько будет всего

кос?

1. 5 грибов в руке несут, 5 грибов в лесу растут, если все грибы собрать, сколько будет как считать?

2. Сколько будет, посчитай-ка, если к 2 прибавить 5 и из суммы 3 отнять.

3. У одной автомашины есть 4 автошины, сколько может автошин быть у 3 автомашин?

4. 4 крыла, а не бабочка, крыльями машет, а не летит (мельница)

5. Имеет 4 зуба, каждый день бывает за столом, но ничего не ест.

6. Кто становится выше, когда садится? (собака)

7. Что становится легче, когда его надувают? (шар)

8. Чем больше берем, тем больше становится (яма)

9. Три брата по дороге бегут, один впереди, два позади, двое задних не могут догнать первого (трехколесный велосипед)

10. На 4 ногах стою, ходить же вовсе не могу (Стол. Стул.)

11. Пять братьев годами равные именами разные (пальцы)

12. Шел человек в город, по дороге встретил трех товарищей. Сколько человек идет в город? (4 человека)

13. Шел человек в город, навстречу три товарища. Сколько человек идет в город ? (1человек т.к. трое шли навстречу)

14. Сидят белки на ветке. Против каждой белки по 2 белки, Сколько всего белок Объясните как сидят белки? (три белки и сидят они треугольником)

39

1. Девочка искала дом № 5. Найдя дом № 1, она не глядя на номера отсчитала 5 домов и вдруг увидела дом № 9. Почему? (дома на улице располагаются по четной стороне и нечетной стороне)

2. В школу шел пятачок нашел, а с товарищем пойду сколько найду?

3. Наташа сказала: «Я получила за контрольную такую оценку, которая получится при сложении и умножении двух одинаковых числа» Что получила Наташа? (4)

4. Предлог стоит в моем начале, в конце же загородный дом, а целое мы все решаем и у доски и за столом (за-да-ча)

5. Лиса поймала 15 окуней и разложила их на 5 кучек так, что в кучках было разное число рыбок. Как она это сделала? (1 + 2 + 3 + 4 + 5 = 15)

6. Выглянув на повороте в окно, Ира увидела впереди 9 вагонов, а следом ещё 7 вагонов. Сколько вагонов в составе? (17)

7. В кучке лежали конфеты. 2 мамы, 2 дочки и бабушка с внучкой взяли по одной штучке. Сколько было конфет в кучке? (3)

8. Ч то за птицы пролетают по 7 в каждый ряд, вереницею летят не воротятся назад (дни недели)

9. Стоят два мальчика. Один смотрит на юг, другой на север. Могут ли они увидеть друг друга, если не употреблять зеркало или другие приспособления? ( могут, если стоят лицом друг к другу.)

10. В жаркий день 6 косцов выпили бочонок кваса за 8 часов. Нужно узнать, сколько косцов за 3 часа выпьют такой же бочонок кваса (за 8 - 6 чел., значит за 1 - 48 чел. Тогда 48 : 3 = 16)

11. Собака усмотрела зайца в 150 саженях от себя. Заяц пробегает за 2 мин. – 500 саженей, а собака за 5 мин. - 1300 саженей. За какое время собака догонит зайца ? (500 : 2 + 250 саж. в мин .заяц 260 – 250 = 10 саж.

1300 : 5 = 260 саж. в мин. собака 150 : 10 = 15 мин. )

55. Лошадь съедает воз сена за месяц, коза - за 2 месяца, овца - за3 месяца. За какое время лошадь, коза и овца съедят воз сена? (за год 12 + 6 + 4 = 22, если 12 месяцев разделить на 22 воза, тогда получится 6/11 месяцев)

1. Путешественник идет из одного города в другой за 10 дней, а второй путешественник этот же путь проходит за 15 дней. Через сколько дней встретятся

40

1. путешественники, если выйдут одновременно навстречу друг другу? (30 : 10 + 30 : 15 = 5 расстояний за месяц, тогда 30 : 5 = 6 дней)

2. Один человек купил 3 козы и заплатил за них 9 рублей. По чём пошла каждая коза? (по дороге)

3. Что это может быть:2 – головы, 6 – ног, а ходят только 4? (всадник)

4. Два землекопа за 2 часа выкопали 2 метра канавы. Сколько землекопов за 5 часов выкопают 5 метров канавы? (2 землекопа)

5. У одного старика спросили: « Сколько тебе лет ? » Он ответил: « Сто лет и несколько месяцев, но дней рождений у меня было всего 25. » Как это может быть? (дед родился 29 февраля)

6. Бочка с капустой на 48 кг тяжелее ящика с консервами. Два ящика с консервами весят 70 кг. Сколько весят 5 бочек с капустой?

7. Определи глубину водоема, если шест длиной 7 метров вбили во дно на 1 метр и выступает он из воды на 2 метра.

8. Хозяйка развела кур и кроликов. Всего 35 голов и 94 ноги. Сколько у хозяйки кур и кроликов? (12 кроликов и 23 курицы)

9. Через 2 года мальчик будет вдвое старше, чем он был 2 года назад, а девочка через 3 года будет втрое старше чем 3 года назад. Кто старше: мальчик или девочка?

10. Три кубика и одна раковина весят столько, сколько 12 бусинок, а одна раковина весит столько же, сколько один кубик и 8 бусин. Сколько бусин надо положить на чашку весов, чтобы уравновесить раковину?

11. Определяя количество воды, даваемое родником, туристы заметили, что двухлитровая банка наполняется за 4 секунды. Сколько воды дает родник за минуту, час, сутки?

12. На складе находились 7 бочонков мёду, 7 наполовину заполненных медом и 7 пустых бочонков. Как распределить все бочонки между тремя покупателями так, чтобы каждый получил одинаковое количество мёда. Причём, мёд не перекладывать.

13. В один кувшин, 3 кружки и 3 стакана вмещается столько же воды, сколько в 2 кувшина и 6 стаканов или в 1 кувшин и 4 кружки. Сколько стаканов воды вмещается в кружку и сколько в кувшин?

41

1. Женщина продавала яйца. Первая покупательница купила у неё половину всех яиц, и еще пол-яйца, вторая купила половину оставшихся яиц и еще пол-яйца, а третья – купила последнее яйцо. Сколько яиц принесла женщина на базар?

2. Который теперь час, если оставшаяся часть суток в 3 раз меньше прошедшей?

3. Сотню орехов хотят разделить на 25 детей так, чтобы каждому досталось нечетное количество. Можно ли это сделать ? Если да, реши, если нет – объясни.

4. Который теперь час, если прошедшая часть суток на 4 часа больше оставшейся?

5. Из 80 деталей одна бракованная. Она легче других. Как найти ее при помощи 4 взвешиваний на двухчашечных весах без гирь?

6. Рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное число кроликов.

7. Коля заметил, что во время липового медосбора пчела улетает из улья со скоростью 4 м/с. И возвращается через 7 минут со скоростью 2 м/с. На каком расстоянии от улья расположена липа, с которой пчела взяла мед? Учесть, что на сбор меда с липы пчела тратит 1 минуту.

8. Бабушке нужно поджарить 6 котлет, а на сковороде помещается всего 5 штук. Каждая котлета жарится 5 минут с одной стороны и с другой стороны. Сколько времени понадобится, чтобы поджарить 6 котлет на одной сковороде. Как это можно сделать за 15 минут?

СОДЕРЖАНИЕ

Пояснительная записка………………………………………………………………1

Особенности развития мышления младших школьников…………………………2

Приёмы развития логического мышления………………………………………….6

Методики, направленные на развитие и определение

степени овладения логическими операциями……………………………………..17

ПРИЛОЖЕНИЕ

Задачи, развивающие логическое мышление………………………………………28

Занимательные вопросы, загадки, смекалки………………………………………..36

ГУ «Ершовская средняя школа»

Развитие логического мышления

младших школьников

методические рекомендации

Учитель начальных классов

Мишура Ольга Анатольевна

2013г

Литература:

1. Брушлинский А.В. Психология мышления и проблемное обучение. – М.: Знание, 1983. – 96 с.

2. БунизеваЛ.С. Методы активизации творческого мышления младших школьников. Начальная школа №3, 2008 год, с.13

3. Винокурова, Н.К. Развиваем способности детей/ Н.К. Винокурова. - М.: РОСМЭН, 2003.- 63с.

4. Гончарова, М.А. Учись размышлять: развитие у детей математических представлений, воображения и мышления: Пособия для начальных классов/ М.А. Гончарова, Е.Э. Кочурова, А.М. Пышкало; Под ред. А.М. Пышкало.- М.: Антал, 2000.- 112с.

5. Гороховская Г.Г. Диагностика уровня сформированности компонентов логического мышления у младших школьников. Н.ш. №6, 2008г. С.40

6. Гребцова Н.И. Развитие мышления учащихся. //Начальная школа. - 1994. - №11. - С.24-27.

7. Зак А.З. Занимательные задачи для развития мышления.//Начальная школа. - 1985. - №5. - С.37-41.

8. Карпова, М. Работаем над развитием мышления школьников/ М.Карпова// Сельская школа.- 2006.- №2.- С.87-94.

9. Манина О.В. Уроки логики как средство развития интеллектуальных и творческих способностей младших школьников.//Н.ш.№4, 2008г., с.63

10. Никифорова Е.Ю. Активизация мыслительной деятельности в процессе работы над задачей//Н.ш.№8, 2008г, с. 45

11. Тамберг Ю.Г. Учись соображать:10 тренингов развития творческого мышления детей. – Екатеринбург: У – Фактория, 2007. – 240с.