Учить мыслить

Учить мыслить,воспитывать интерес к математике.

         Математика – основа техники и теории всех естественных наук. Успехи многих наук  в значительной степени зависят от применения в этих  науках математических методов и теорий.

          Все это говорит   о необходимости  проведения систематической и упорной работы учителей по повышению математических знаний учащихся . Однако повышение матема- тической подготовки учащихся не будет успешным без использования тех богатых воспи- тательных  средств , которыми располагает математика . Многие замечательные  люди  в  различной форме высказывали, что математика дисциплинирует ум, приучает к логичес- кому мышлению,что она является гимнастикой ума. Математика воспитывает тех , кто ее изучает, неопровержимостью своих выводов.

       Изучение математики способствует развитию внимания,наблюдательности,воспиты- вает аккуратность ,настойчивость и упорство в достижении цели . Изучение математики , особенно  геометрии , содействует развитию простраственного  воображения , т.е. таких свойств ума, которые очень нужны художникам,архитекторам,конструкторам, летчикам   и т.д.

       Чтобы вызвать интерес к математике,применяются различные формы работы как на уроках, так и на внеклассных занятиях. К ним относятся:

1. проведение математических диктантов в 5-8 кпассах;
2. решение занимательных и исторических задач;
3. решение задач различными способами;
4. разбор математических софизмов;
5. проведение заочных математических конкурсов с поощрением победителей;
6. знакомство  учащихся с  жизнью  и  деятельностью выдающихся математиков  

(Архимед,Ньютон,Лобачевский,Ковалевская и другие);

1. проведение математических вечеров с викторинами,инсценировками-шутками,

математическими играми и др.;

1. заслушивание докладов на математических кружках ( о теореме Пифагора, о

числе π, о формуле Симпсона и др.);

1. выпуск стенной газеты «Математика и жизнь»,
2. разбор задач повышенной трудности;
3. проведение экскурсий с показом применения математики в жизни;
4. сообщение исторических справок в процессе прохождения программы;
5. выполнение учащимися домашних сочинений по математике;
6. индивидуальная работа с  учащимися на уроках и вне их;
7. широкое использования научно-популярной,методической и художественной

литературы и интернет.

Примеры из опыта работы:

       Чтобы вызвать интерес к математике,применяются различные формы работы как на уроках, так и на внеклассных занятиях. К ним относятся:

1. проведение математических диктантов в 5-8 кпассах;
2. решение занимательных и исторических задач;
3. решение задач различными способами;
4. разбор математических софизмов;
5. проведение заочных математических конкурсов с поощрением победителей;
6. знакомство  учащихся с  жизнью  и  деятельностью выдающихся математиков  

(Архимед,Ньютон,Лобачевский,Ковалевская и другие);

1. проведение математических вечеров с викторинами,инсценировками-шутками,

математическими играми и др.;

1. заслушивание докладов на математических кружках ( о теореме Пифагора, о

числе π, о формуле Симпсона и др.);

1. выпуск стенной газеты «Математика и жизнь»,
2. разбор задач повышенной трудности;
3. проведение экскурсий с показом применения математики в жизни;
4. сообщение исторических справок в процессе прохождения программы;
5. выполнение учащимися домашних сочинений по математике;
6. индивидуальная работа с  учащимися на уроках и вне их;
7. широкое использования научно-популярной,методической и художественной

литературы и интернет.

Примеры из опыта работы:

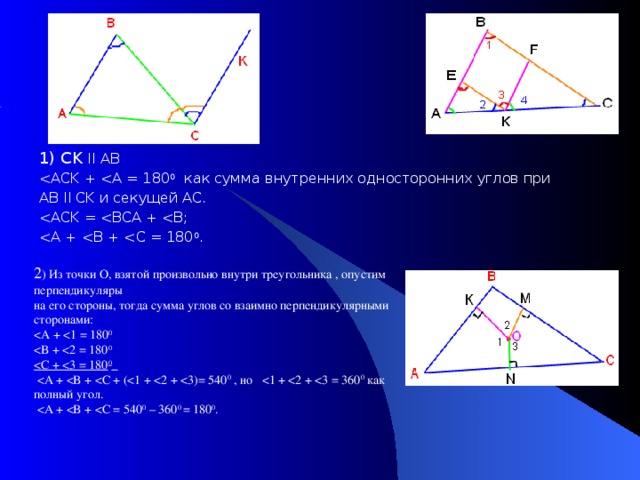
1.   CK II AB
2. ACK + <A = 1800  как сумма внутренних односторонних углов при AB II CK и секущей АС.

<ACK = <BCA + <B;

<A + <B + <C = 1800.

1.  Из точки О, взятой произвольно внутри треугольника , опустим перпендикуляры

на его стороны, тогда сумма углов со взаимно перпендикулярными сторонами:

• A + <1 = 1800
• B + <2 = 1800
• C + <3 = 1800 
• A + <B + <C + (<1 + <2 + <3)= 5400 , но   <1 + <2 + <3 = 3600 как полный угол.
• A + <B + <C = 5400 – 3600 = 1800.                                                                                                                  Несколько примеров из работы в старших классах.

1. а и в катеты, с- гипотенуза. Доказать , что r =  (a+b-c).(r-радиус вписанной окр.)  

Доказательство:

 1-способ.  S =    ab = pr =  (a+b+c)r  =>  r =      (1)

 По теореме Пифагора  a2+ b2 = c2 , или  (a+b)2 -2ab = c2. Отсюда,  2ab  = (a+b)2  -  c2 = 

=(a+b+c)(a+b-c). Cледовательно,  из  (1)  =>   r =   =   =    .

2-способ.   AC=b,BC=a и AB=c. Проведем радиусы OD,OE и OF. Тогда OD | AC, OF | BC ,        OE | AB. Значит, CDOF –  квадрат,  AD = AC – CD = b – r,  BF = BC – FC = a – r. Но AD = AE и     BF = BE .

 AE = b – r, BE = a – r  и  AB = AE + BE  =>  c = (b-r) + (a-r),    r =  (a+b-c).

1. Доказать , что площадь прямоугольного треугольника можно найти по формуле

S=(2R+r)r , где R и r – радиусы описанной и вписанной окружности.

Доказателство:

1-способ.    Пусть  АВС-данный прямоугольный треугольник, <C = 900  и  OM=ON=OK =r-

радиус вписанной окружности. Тогда AB=2R,  SABC=pr, где p –полупериметр.

               AC + BC = 2r + AB , так как  СA  , СB - касательные проведенные из одной точки.

Следовательно, SABC= pr=  r = (r+AB)r = (r+2R)r.

2-способ.

 ?АВС-прямоугольный , AB = 2R  и  S =  AC BC . Пусть  AC = x , BC = y. SABC = xy .

 ?ABC => x2 + y2 = 4R2  . Так как  r =  (AC+BC- AB) =  (x+y-2R) и  x+y=2(R+r), то =>  (x+y)2 – 2xy =4R2,  4(R+r)2 – 2xy = 4R2, отсюда   xy = (R+r)2 – R2,

или S? =r(2R+r).

     6.Синус суммы двух аргументов.

sin(α+β)=sinα cosβ + cosα sinβ.

Доказываем так:

SABC=  a c sin(α+β),    SABD=  hb c sinα,   SBDC =   hb a sinβ.

SABC= SABD + SBCD  =>      a c sin(α+β) =  hb c sinα +   hb a sinβ.

 Делим обе части данного равенства на      ac,

sin(α+β)= sinα +  sinβ, но    = cosβ  из ?BCD ,    = cosα  из ?ABD. Следовательно,    sin(α+β)=sinα cosβ + cosα sinβ.