Презентация к уроку геометрии по теме "Центральные углы и углы, вписанные в окружность". Основная цель - расширить сведения об окружности и ввести новые важные понятия, связанные с окружностью.
Данный материал можно использовать при изучении нового материала, повторении данной темы и подготовке к ГИА.
Какие задачи использовать на уроке, решает учитель.
В зависимости от подготовки учащихся часть номеров можно использовать для устной работы, часть для письменной.
Просмотр содержимого презентации
«Центральные углы и углы, вписанные в окружность»

- Центральные углы и углы, вписанные в окружность
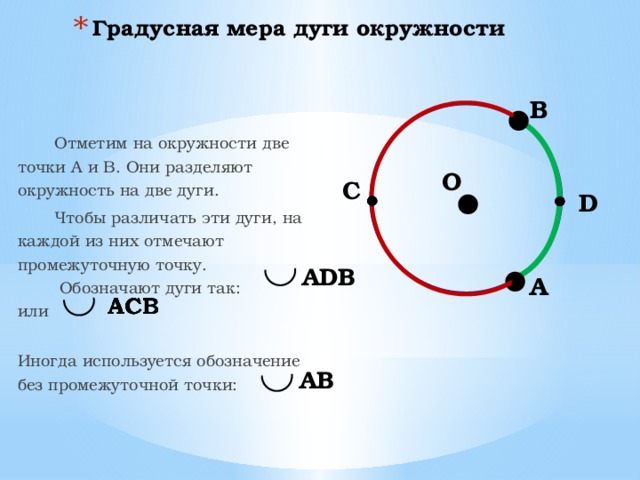
- Градусная мера дуги окружности
∙
В
Отметим на окружности две точки А и В. Они разделяют окружность на две дуги.
Чтобы различать эти дуги, на каждой из них отмечают промежуточную точку.
Обозначают дуги так:
или
Иногда используется обозначение без промежуточной точки:
∙
О
С
D
∙
АDВ
А
АВ
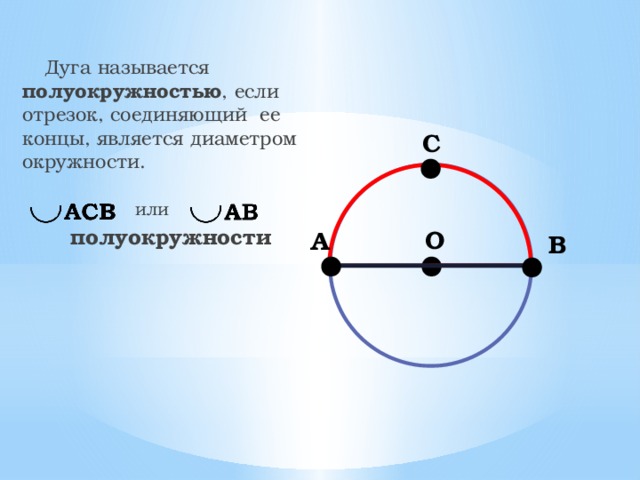
Дуга называется полуокружностью , если отрезок, соединяющий ее концы, является диаметром окружности.
или
полуокружности
∙
С
∙
∙
∙
О
А
В
∙
D
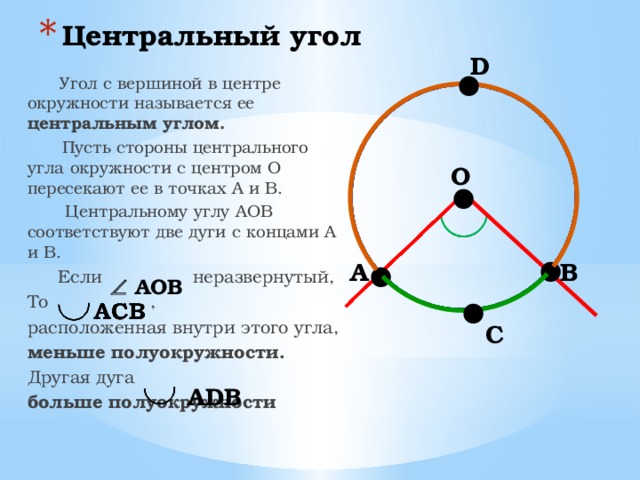
Угол с вершиной в центре окружности называется ее центральным углом.
Пусть стороны центрального угла окружности с центром О пересекают ее в точках А и В.
Центральному углу АОВ соответствуют две дуги с концами А и В.
Если неразвернутый,
То ,
расположенная внутри этого угла,
меньше полуокружности.
Другая дуга
больше полуокружности
∙
О
∙
∙
А
В
∙
АОВ
С
АDВ
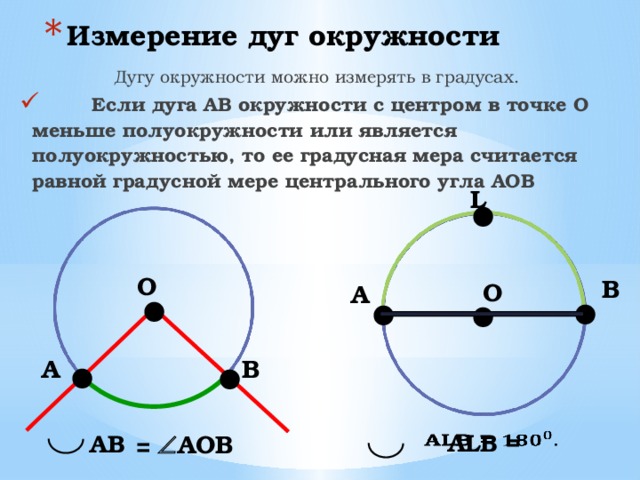
Дугу окружности можно измерять в градусах.
- Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ
∙
L
∙
∙
∙
∙
О
В
О
А
∙
∙
А
В
АLВ =
АВ
= АОВ
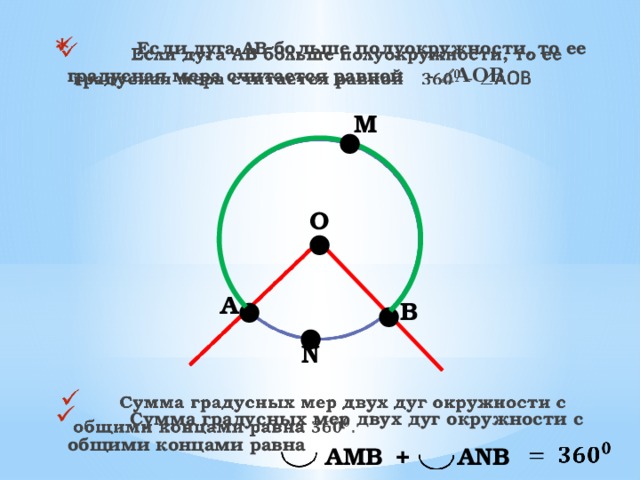
- Если дуга АВ больше полуокружности, то ее градусная мера считается равной - АОВ
- Сумма градусных мер двух дуг окружности с общими концами равна
∙
M
∙
О
∙
∙
А
∙
В
N
АMВ
АNВ
+
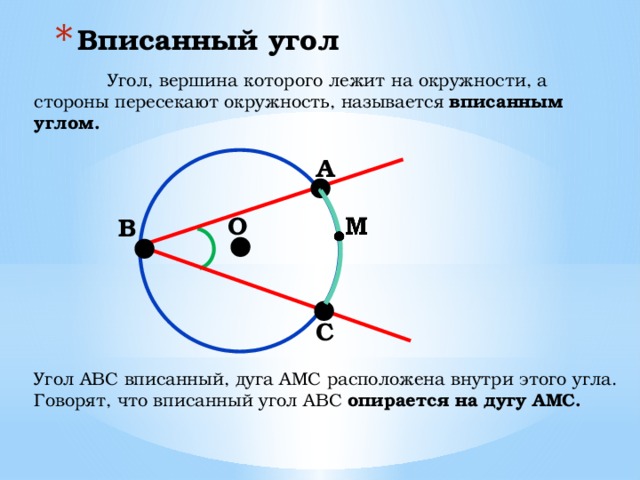
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Угол АВС вписанный, дуга АМС расположена внутри этого угла.
Говорят, что вписанный угол АВС опирается на дугу АМС.
∙
А
∙
∙
О
В
∙
С
∙
С
∙
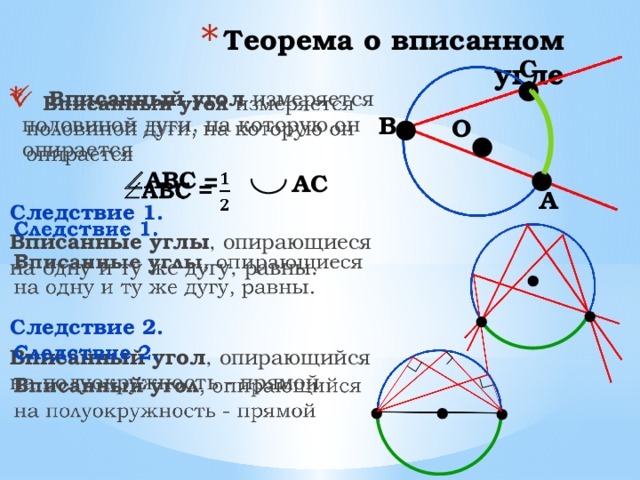
- Вписанный угол измеряется половиной дуги, на которую он опирается
АВС =
Следствие 1.
Вписанные углы , опирающиеся на одну и ту же дугу, равны.
Следствие 2.
Вписанный угол , опирающийся на полуокружность - прямой
∙
В
О
∙
АС
А
∙
∙
∙
∙
∙
∙
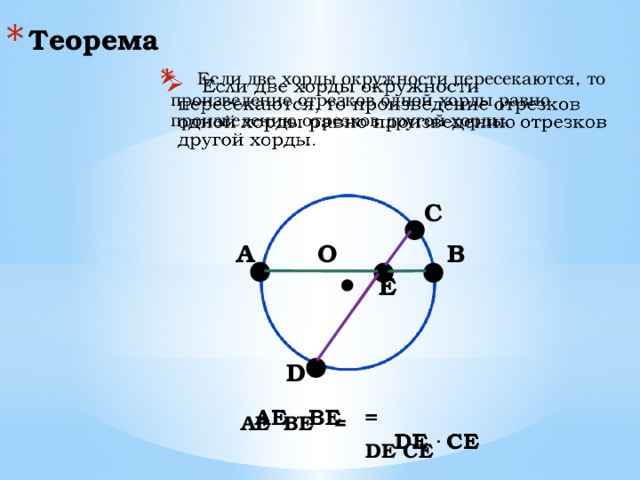
- Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
AE BE =
DE CE
∙
С
∙
∙
∙
А
В
О
∙
E
∙
D

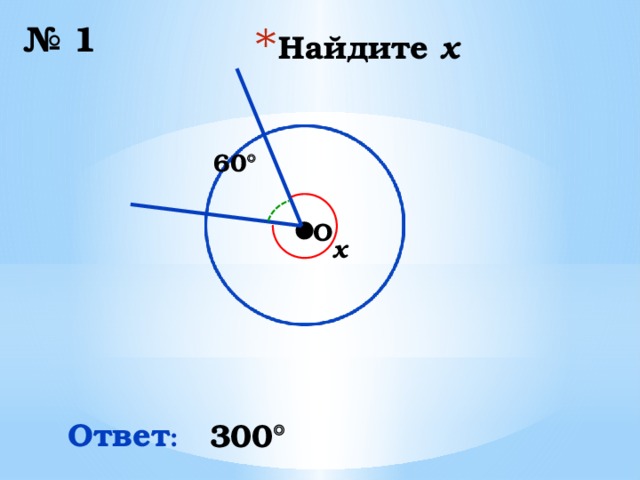
№ 1
60
∙
O
x
Ответ :
300
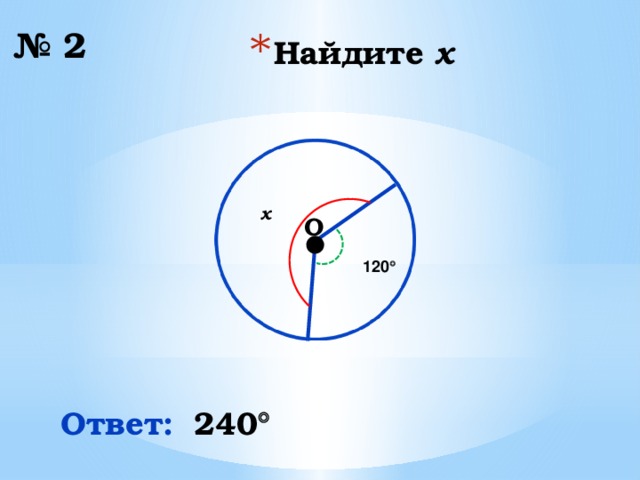
№ 2
∙
x
O
120
Ответ:
240
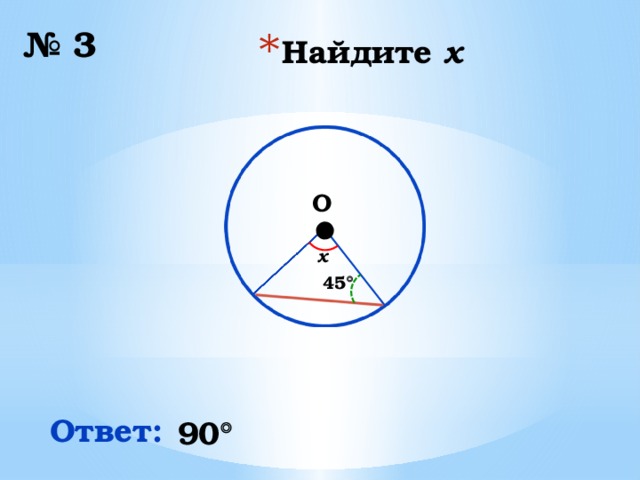
№ 3
∙
O
x
45
Ответ:
90
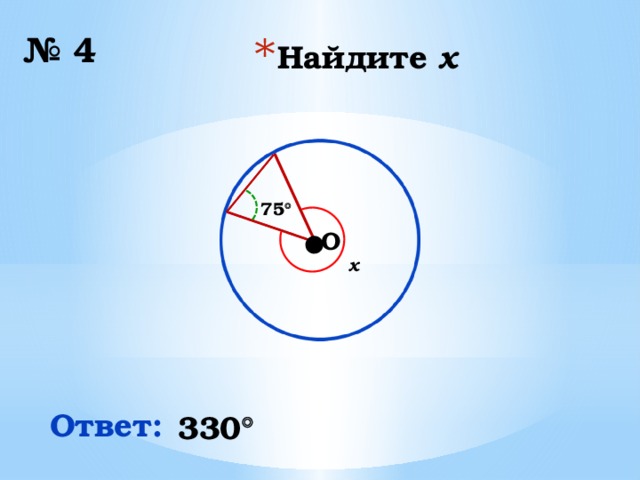
№ 4
75
∙
O
x
Ответ:
330
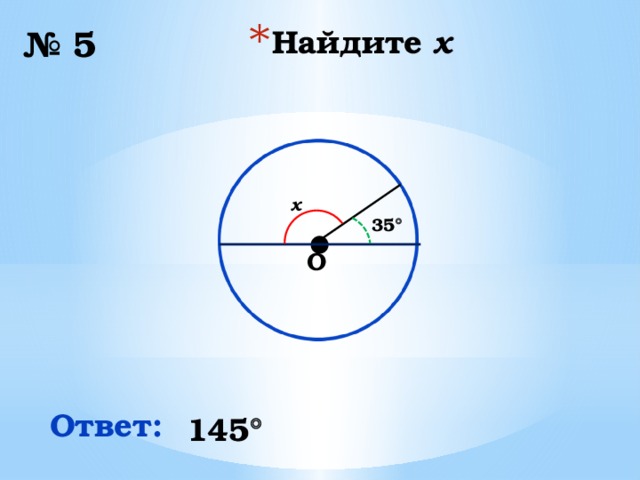
№ 5
x
∙
35
O
Ответ:
145
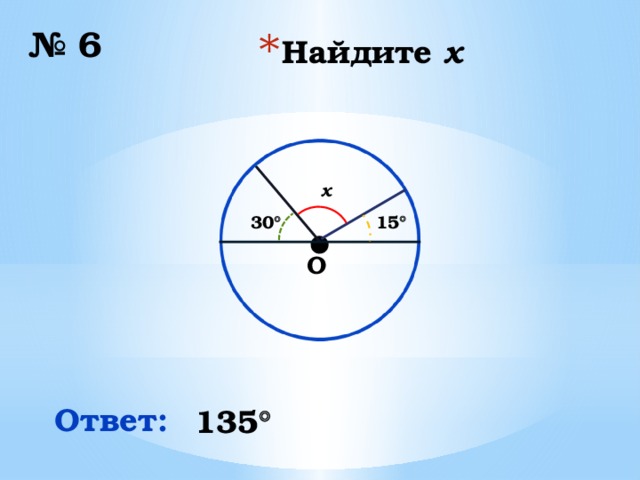
№ 6
x
∙
15
30
O
Ответ:
135
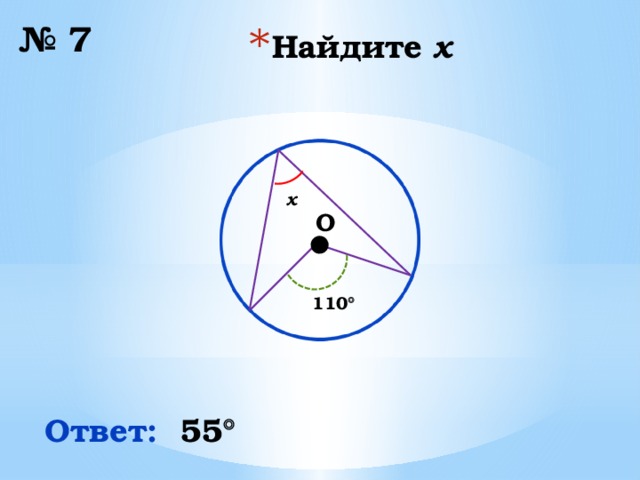
№ 7
x
∙
O
110
Ответ:
55
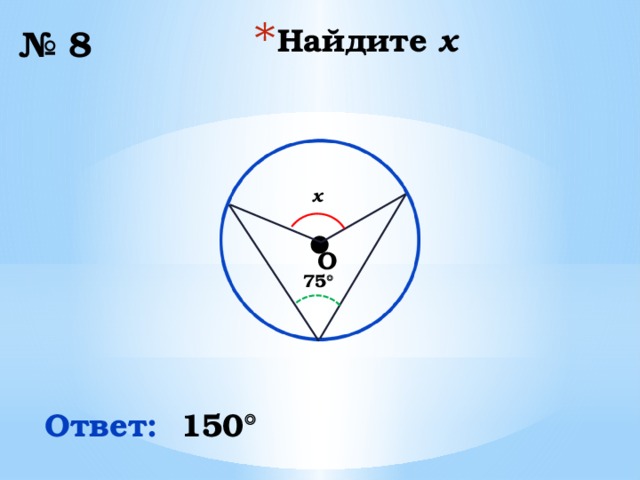
№ 8
x
∙
O
75
Ответ:
150
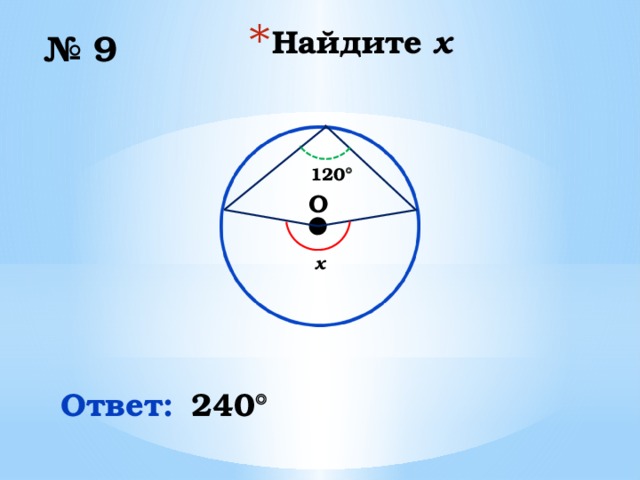
№ 9
120
∙
O
x
Ответ:
240
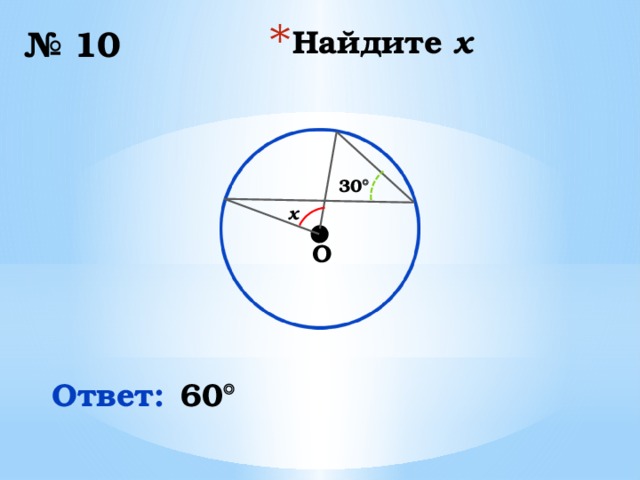
№ 10
30
∙
x
O
Ответ:
60
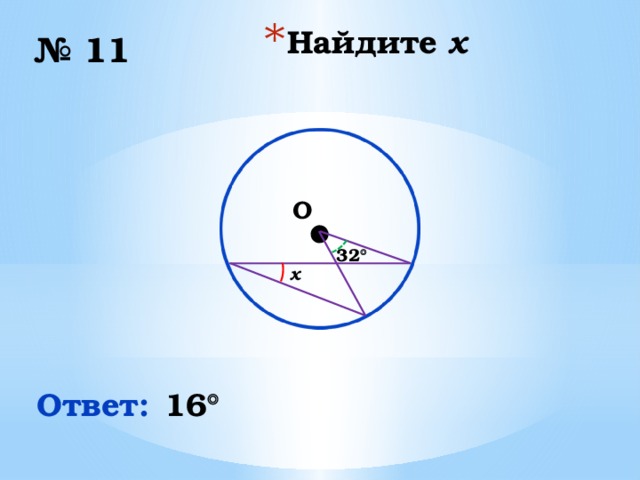
№ 11
∙
O
32
x
Ответ:
16
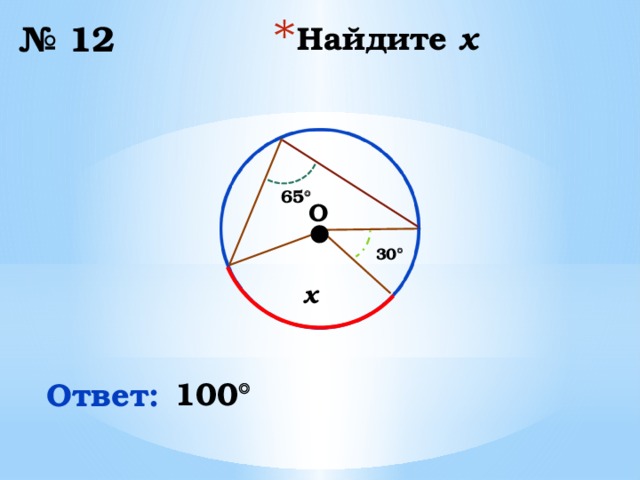
№ 12
65
∙
O
30
x
100
Ответ:
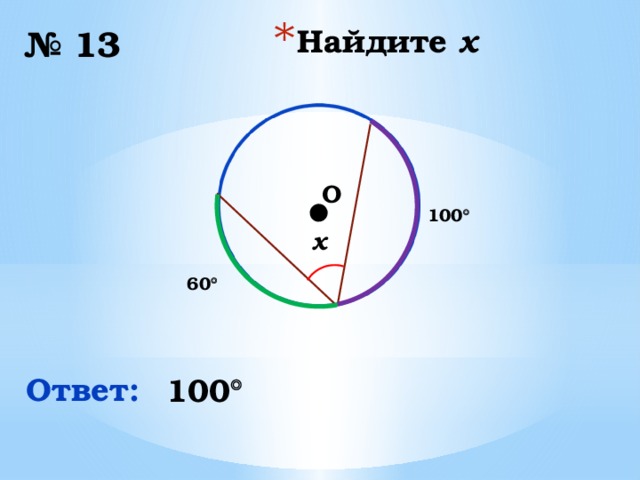
№ 13
∙
O
100
x
60
Ответ:
100
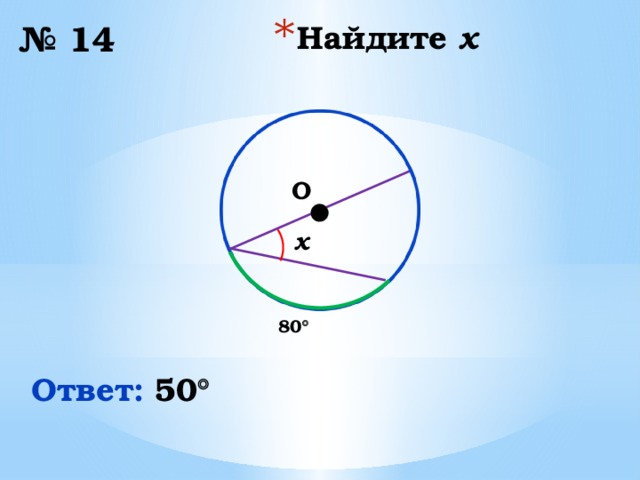
№ 14
∙
O
x
80
Ответ:
50
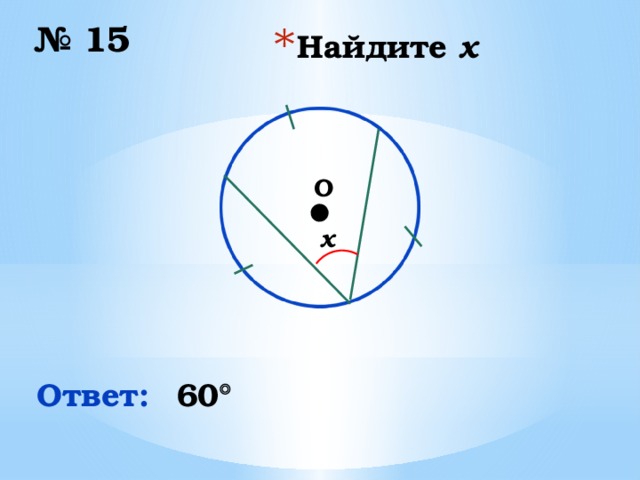
№ 15
∙
O
x
Ответ:
60
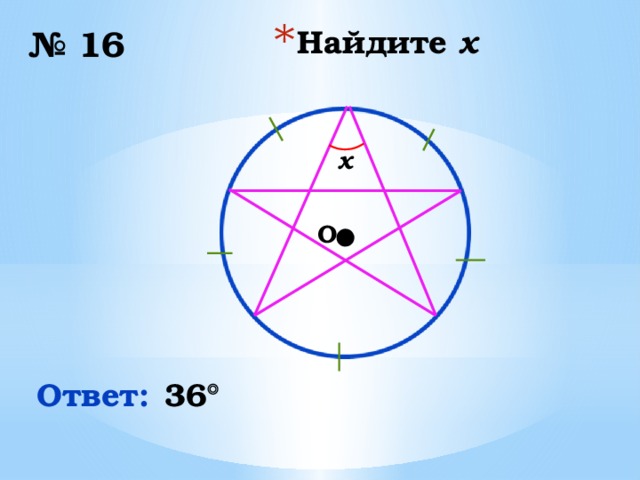
№ 16
x
∙
O
36
Ответ:
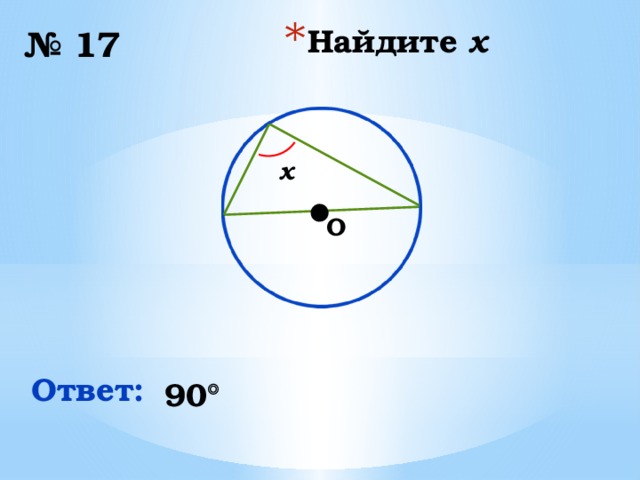
№ 17
x
∙
O
Ответ:
90
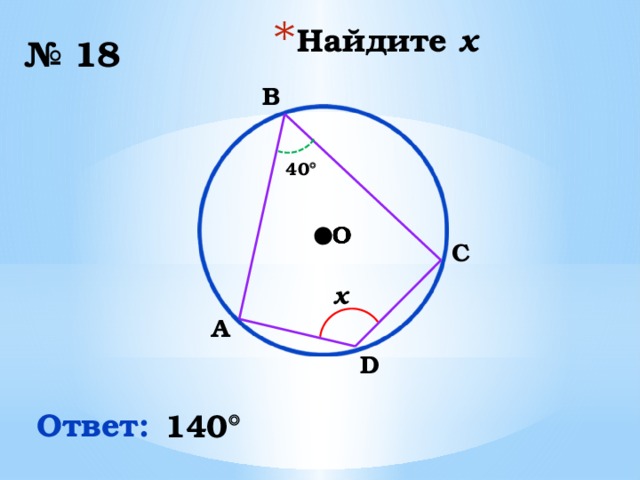
№ 18
B
40
∙
C
x
A
D
Ответ:
140
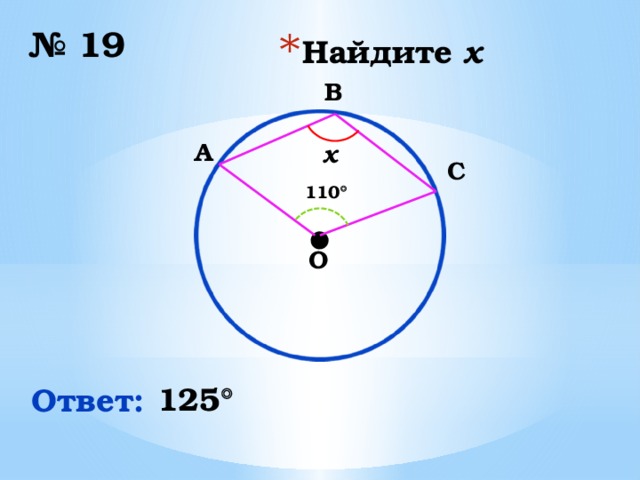
№ 19
B
A
x
C
110
∙
O
125
Ответ:
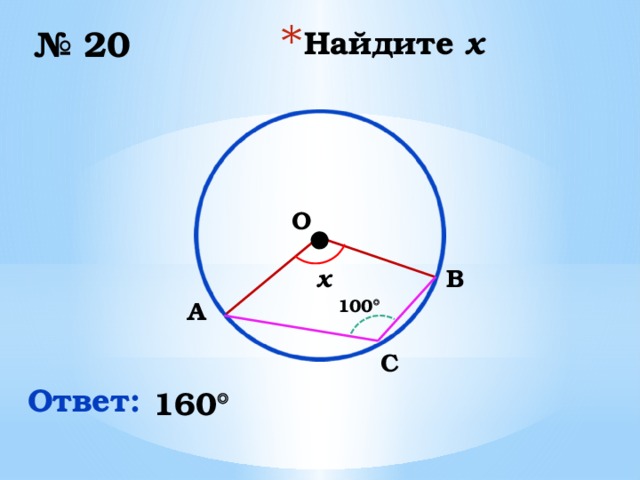
№ 20
∙
O
B
x
100
A
C
Ответ:
160
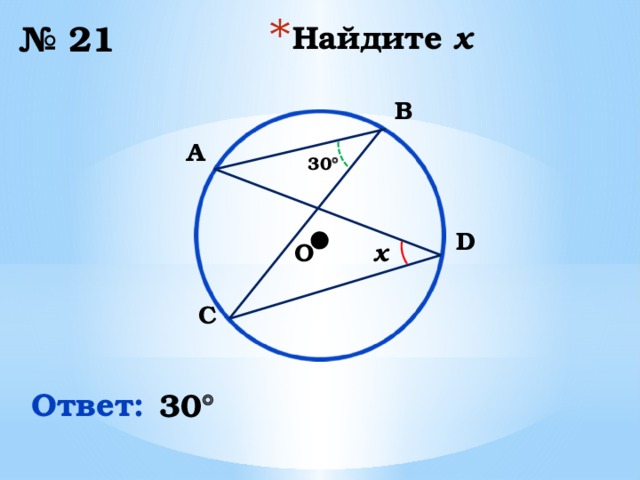
№ 21
B
A
30
∙
D
x
O
C
Ответ:
30
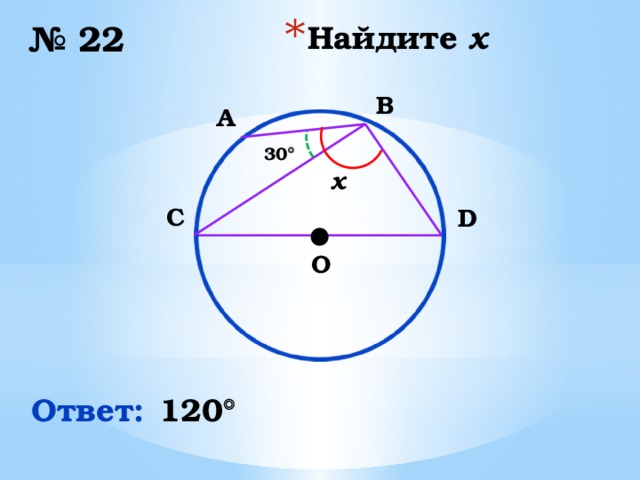
№ 22
B
A
30
x
∙
C
D
O
120
Ответ:
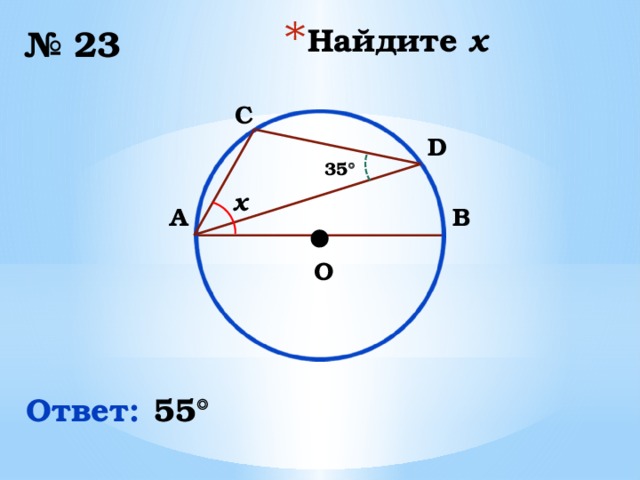
№ 23
C
D
35
x
∙
B
A
O
Ответ:
55
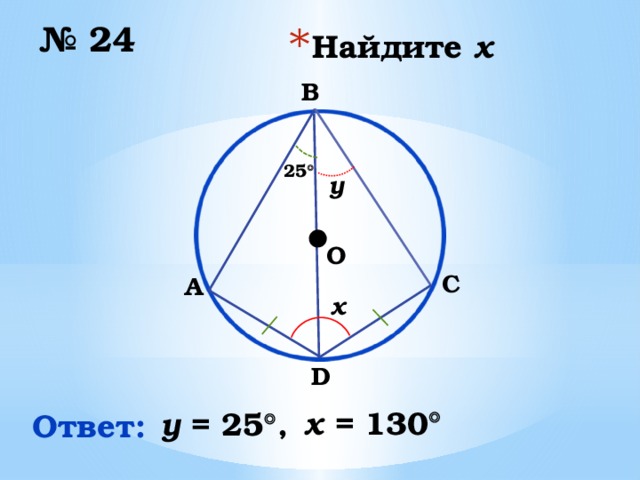
№ 24
B
25
y
∙
O
C
A
x
D
x = 130
y = 25 ,
Ответ:
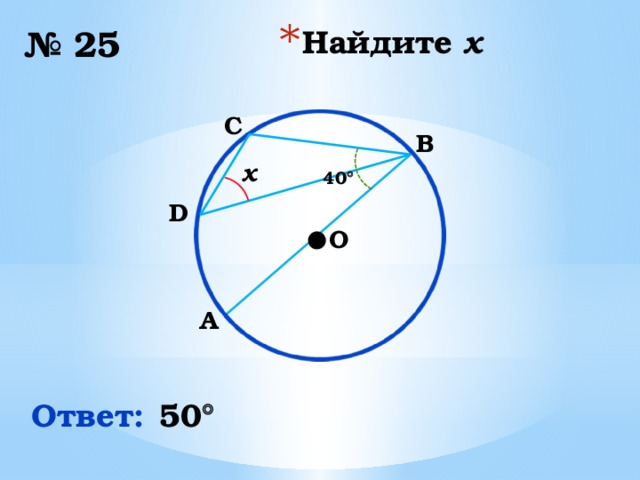
№ 25
C
B
x
40
∙
D
O
A
50
Ответ:
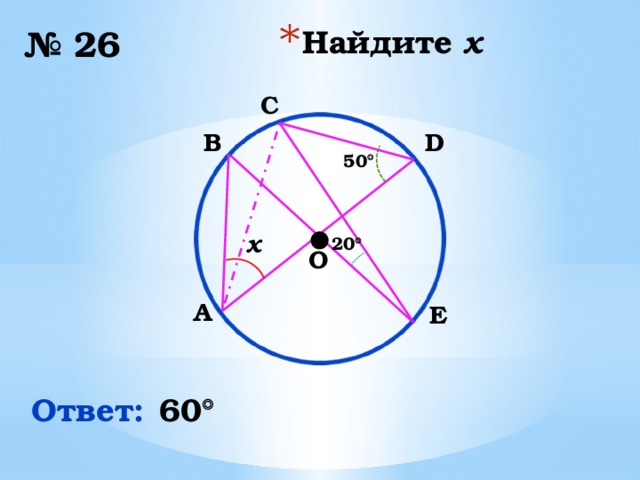
№ 26
C
B
D
50
∙
x
20
O
A
E
Ответ:
60

- Данный материал можно использовать при изучении нового материала, повторении данной темы и подготовке к ГИА.
- Какие задачи использовать на уроке, решает учитель.
- В зависимости от подготовки учащихся часть номеров можно использовать для устной работы, часть для письменной.





















































