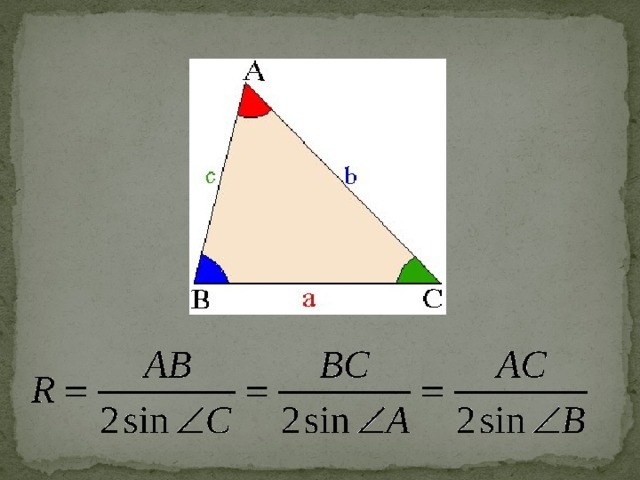
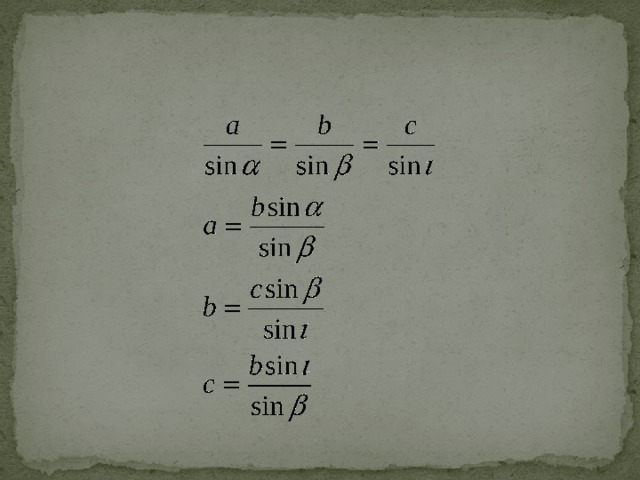Теоре?ма си?нусов — теорема, устанавливающая зависимость между сторонами треугольника и противолежащими им углами. Существуют два варианта теоремы; обычная теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.?Самое древнее доказательство для теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике» написанной в XIII веке. Теорема синусов для сферического треугольника была доказана математиками средневекового Востока ещё в X векеВ труде Ал-Джайяни XI века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Теорема синусов
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Теорема синусов »
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
2710 руб.
2220 руб.
3170 руб.
1230 руб.
1760 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства