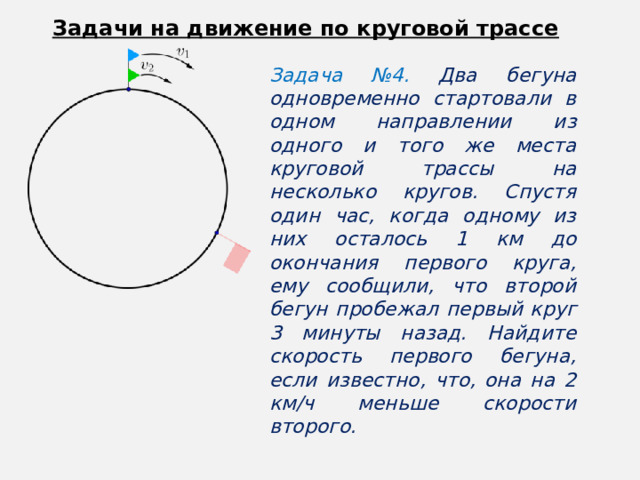
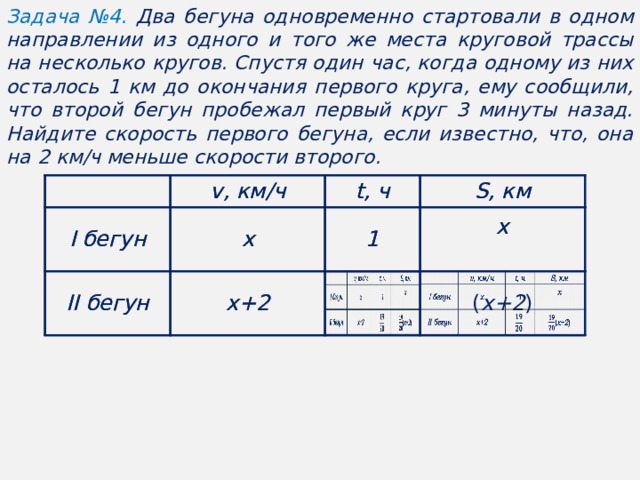
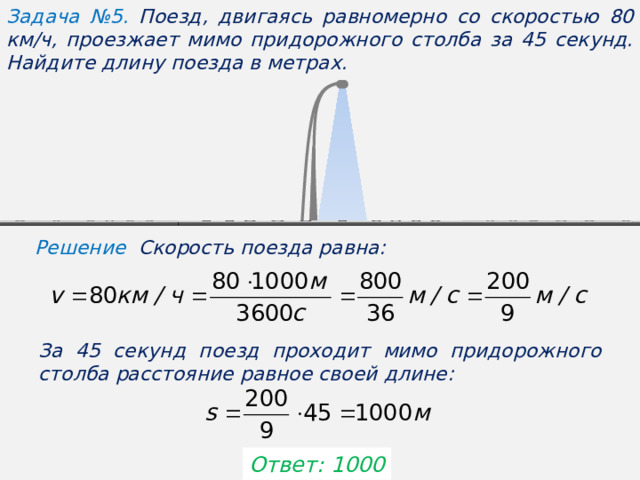
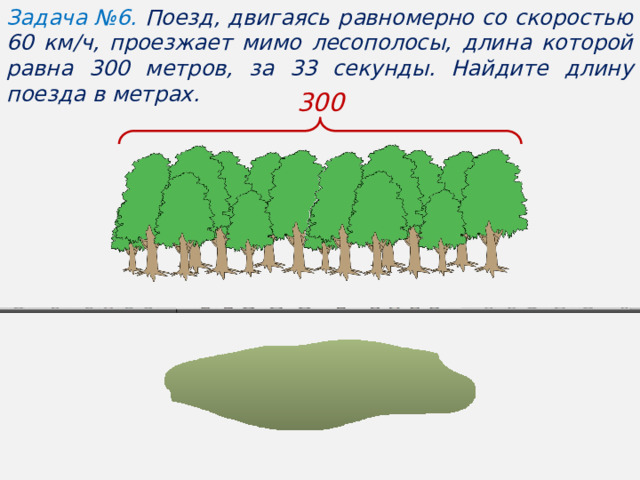
Текстовые задачи являются традиционным разделом на экзамене по математике.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Решение текстовых задач при подготовке к ОГЭ 2022-2023. Задание 21
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение текстовых задач при подготовке к ОГЭ 2022-2023. Задание 21»
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1430 руб.
2380 руб.
1900 руб.
3170 руб.
1490 руб.
2480 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства




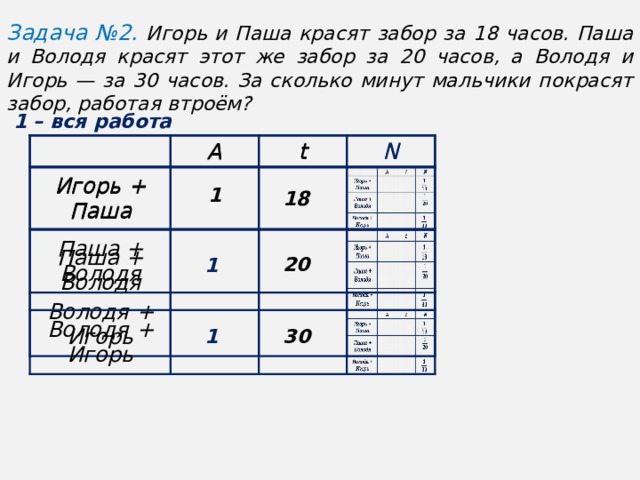
 0). A Ученик Ученик A 231 дет. 231 дет. Мастер N Мастер N t t ч. ч. x дет/ч 462 дет. (x+4) дет/ч Зная, что ученик потратил на работу на 11 часов больше, составим и решим уравнение:" width="640"
0). A Ученик Ученик A 231 дет. 231 дет. Мастер N Мастер N t t ч. ч. x дет/ч 462 дет. (x+4) дет/ч Зная, что ученик потратил на работу на 11 часов больше, составим и решим уравнение:" width="640"