Данная работа представлена в форме презентации с использованием наглядной анимации для демонстрации процесса решения задач. Созданная презентация должна привлечь внимание выпускников к решению геометрических хадач; заинтересовать учителей математики, предоставив им презентацию как пособие для занятий с учениками при подготовке к ЕГЭ.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
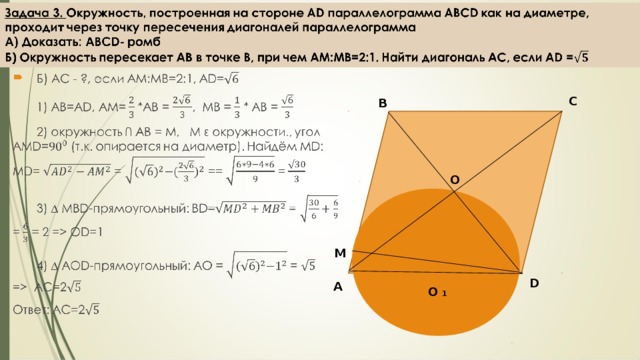
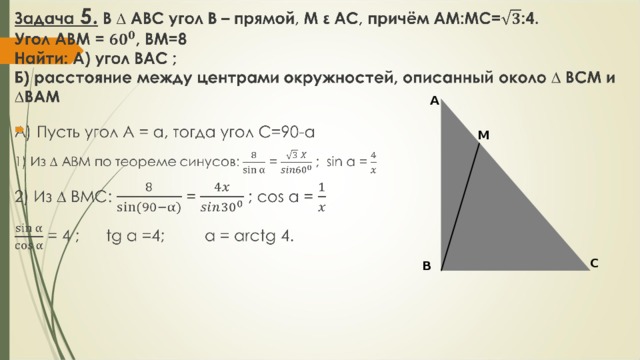
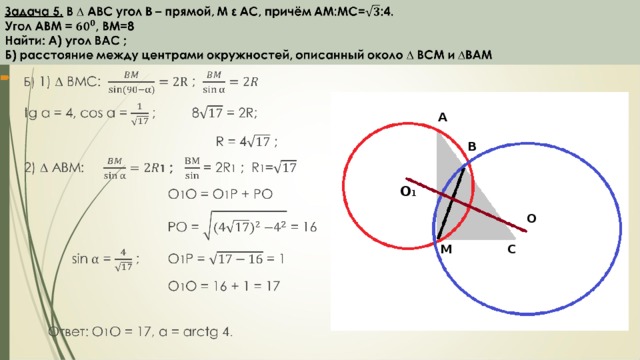
Решение геометрических заданий С4 ЕГЭ 2014
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение геометрических заданий С4 ЕГЭ 2014 »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1720 руб.
2860 руб.
1430 руб.
2380 руб.
1540 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



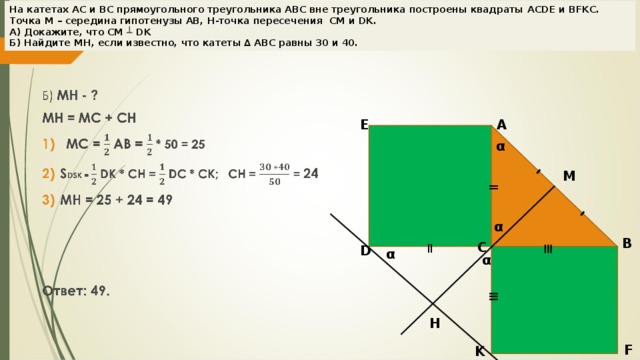
 угол А = углу CDK = α CM – медиана прямоугольного ∆ АВС = AM = CM = ∆ AMC – равнобедренный, углы при основании равны = угол ACM = α 2) Угол ACM = углу HCK = α , так как вертикальные, угол CKD = 90 – α , тогда угол CHK = 180 – α – ( 90 – α ) = 90 Значит CM ┴ DK . Ч.Т.Д α M = α B C D α α ≡ H F K" width="640"
угол А = углу CDK = α CM – медиана прямоугольного ∆ АВС = AM = CM = ∆ AMC – равнобедренный, углы при основании равны = угол ACM = α 2) Угол ACM = углу HCK = α , так как вертикальные, угол CKD = 90 – α , тогда угол CHK = 180 – α – ( 90 – α ) = 90 Значит CM ┴ DK . Ч.Т.Д α M = α B C D α α ≡ H F K" width="640"