Групповое занятие (группа риска) по теме «Решение простейших геометрических задач».zip

Павлова А.С., Учитель первой квалификационной категории

Групповое занятие (группа риска) по теме

«Решение простейших геометрических задач»

Класс:11

Учитель: Павлова А.С., первая квалификационная категория.

МАОУ «СОШ №8» г .Гая

Цель:

• напомнить учащимся теоретические аспекты решения простейших геометрических задач (синус, косинус, тангенс), показать основной способ решения геометрических задач;

• воспитывать познавательный интерес к предмету за счет использования разнообразных форм работы;

• развивать самостоятельность при выполнении тестовых заданий

Оборудование: компьютеры, проектор, комп. тест и презентация

Структура занятия:

1. Постановка темы, цели занятия (мотивация) -2 мин.

2. Изучение нового материала (теоретические аспекты). – 8 мин.

3. Закрепление нового материала – 15 мин

4. Проверка усвоения изученного материала -12 мин

5. Постановка домашнего задания. Подведение итогов урока -3 мин

Ход занятия

1. Постановка темы, цели занятия (мотивация)

Сегодня мы с вами будем продолжать подготовку к ЕГЭ и разберем задание В4.

1. Изучение нового материала (теоретические аспекты).

Учащимся под диктовку даются основные определения и тождества

1. Закрепление нового материала

Учащимся предлагается выполнить 3 задания: 1 задание – объясняет учитель, учащиеся записывают под диктовку, 2 и 3 задание – учащиеся решают у доски, учитель комментирует ход решения.

1. Проверка усвоения изученного материала

Учащимся предлагается выполнить тестовое задание на компьютере: задание содержит 5 вопросов.

1. Постановка домашнего задания. Подведение итогов урока.

Учащимся раздаются карточки с домашними задачами.

Вопросы:

1. Что называется синусом острого угла прямоугольного треугольника?

2. Что называется косинусом острого угла прямоугольного треугольника?

3. Что называется тангенсом острого угла прямоугольного треугольника?

Резервное задание: Для учащихся, которые справились со всеми предложенными заданиями теста быстрее всех раздаются карточки с задачами

Список использованной литературы

1. Гордин Р. К. ЕГЭ 2011. Математика. Задача С4. Геометрия. Планиметрия / Под ред. А. Л. СЕМЕНОВА И И. В. ЯЩЕНКО. — М.: МЦНМО, 2011. —148 с

2. КЛОВО А. Г. Математика: интенсивный курс подготовки к ЕГЭ / А. Г. Клово. — Ростов н/Д: Феникс, 2011. — 185

3. Семенов, А.Л. ЕГЭ: 3000 задач с ответами по математике. Все задания группы В / А.Л. Семенов, И.В. Ященко.-- М.: Издательство «Экзамен», 2011. — 511

Домашнее задание

Задание №1

Задание №2

Домашнее задание

Задание №1

Задание №2

Домашнее задание

Задание №1

Задание №2

Дополнительное задание

Задание №1

Дополнительное задание

Задание №1

Дополнительное задание

Задание №1

Дополнительное задание

Задание №1

Дополнительное задание

Задание №1

Дополнительное задание

Задание №1

Решение простейших геометрических задач (В4)

Групповое занятие (группа риска)

Учитель: Павлова А.С.

Учитель математики, информатики

МАОУ «СОШ №8» г. Гая

sin

cos

tg

sin

cos

tg

sin

cos

tg

sin

cos

tg

Определение синуса

острого угла прямоугольного треугольника

Синус острого угла прямоугольного треугольника равен отношению противолежащего к данному острому углу катета и гипотенузы

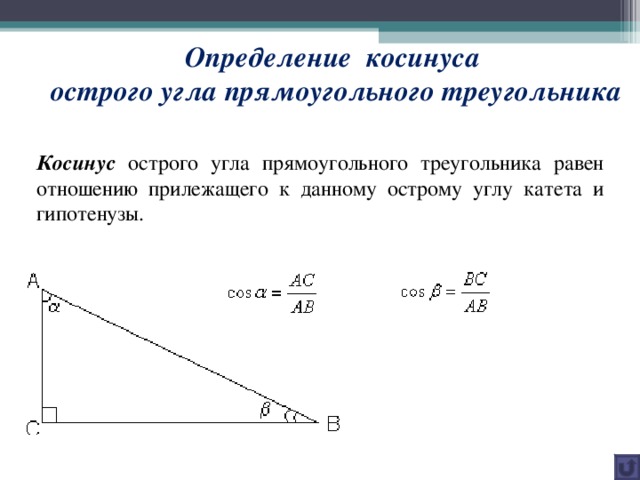
Определение косинуса

острого угла прямоугольного треугольника

Косинус острого угла прямоугольного треугольника равен отношению прилежащего к данному острому углу катета и гипотенузы.

Определение тангенса

острого угла прямоугольного треугольника

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего к данному острому углу катета к прилежащему.

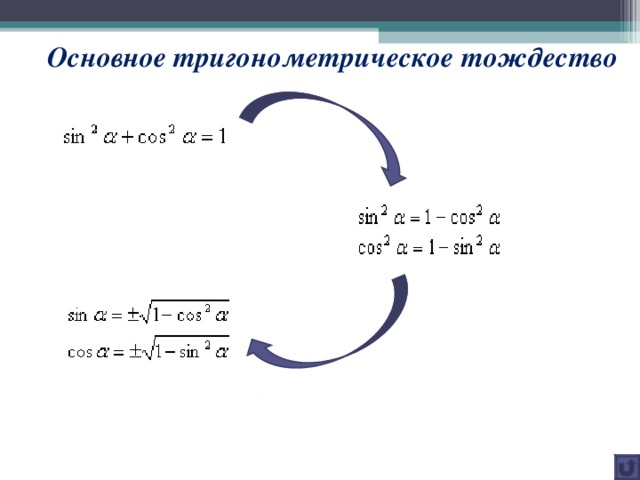
Основное тригонометрическое тождество

Задание В4 .

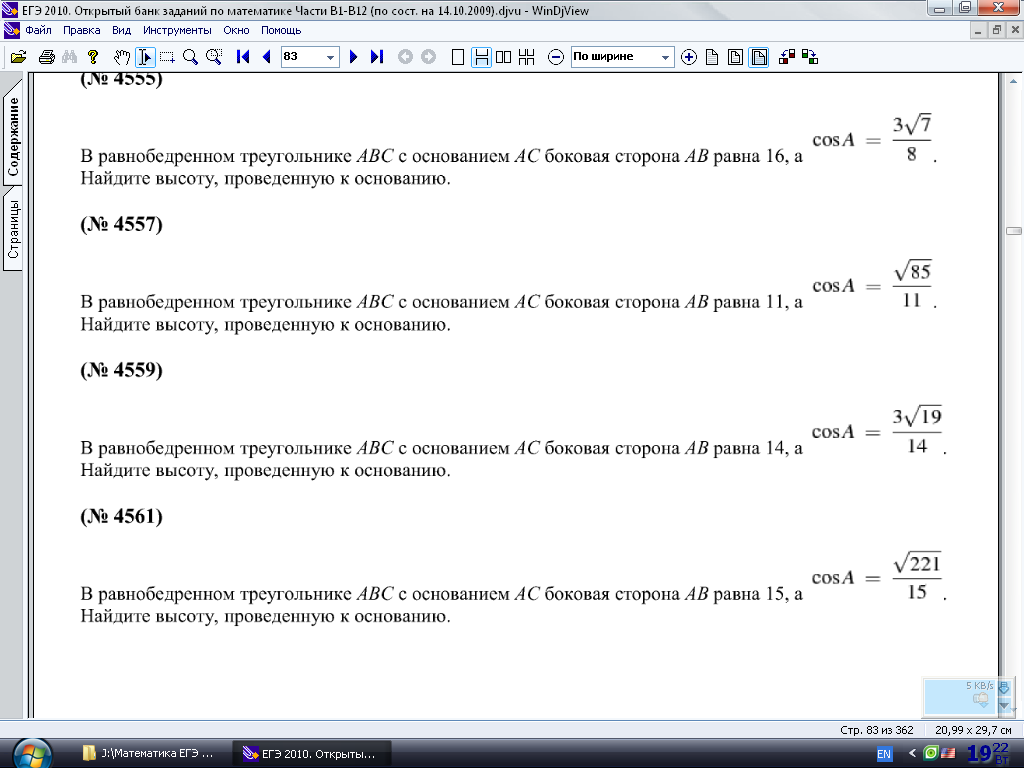
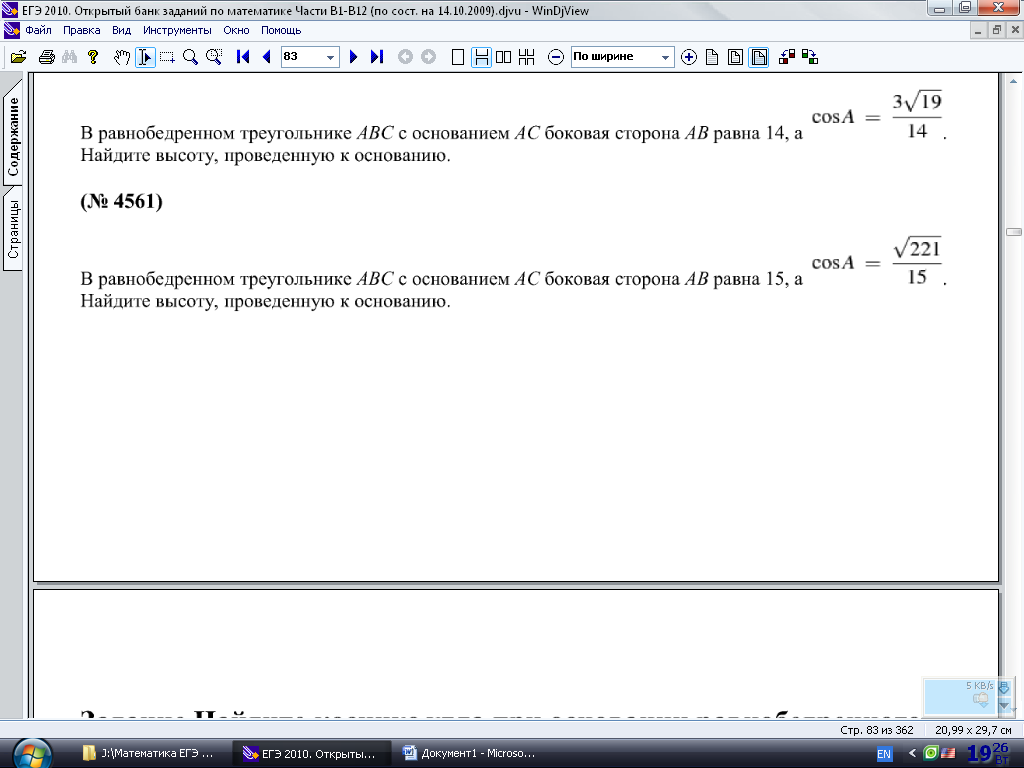
Задания на нахождение высоты равнобедренного треугольника, проведенного к его основанию, если известен косинус угла при основании

Задание №1 В равнобедренном треугольнике АВС с основанием АС боковая сторона АВ равна 8, а . Найдите высоту треугольника.

Дано: АВС - р/б треугольник

АВ = 8

Найти: ВН

Решение: Рассмотрим АВН – прямоугольный треугольник, т.к. ВН – высота р/б треугольника АВС.

В

С

А

Н

Ответ: 6

Задание №2 В равнобедренном треугольнике АВС с основанием АС боковая сторона АВ равна 15, а . Найдите высоту треугольника.

Дано: АВС - р/б треугольник

АВ = 8

Найти: ВН

Решение: Рассмотрим АВН – прямоугольный треугольник, т.к. ВН – высота р/б треугольника АВС.

В

С

А

Н

Ответ: 1

Задание №3 В равнобедренном треугольнике АВС с основанием АС боковая сторона АВ равна 11, а . Найдите высоту треугольника.

Дано: АВС - р/б треугольник

АВ = 8

Найти: ВН

Решение: Рассмотрим АВН – прямоугольный треугольник, т.к. ВН – высота р/б треугольника АВС.

В

С

А

Н

Ответ: 6