Развитие мотивации к учебной деятельности на уроках математики

Развитие мотивации к учебной деятельности на уроках математики. Докладчик: учитель математики МОУ ООШ с.Брянкустичи Таранова Н.А.

• МОТИВАЦИЯ (от англ. « movere » - «двигать»)- процессы, методы, средства побуждения учащихся к продуктивной познавательной деятельности, активному освоению содержания образования.
• Роль учителя в создании мотивов обучения является одной из главных.

В психологии известно, что развитие мотивов учения идет двумя путями:

• Через усвоение учащимися общественного смысла учения;

2. Через саму деятельность учения школьника, которая должна чем-то заинтересовать его.

Условия, вызывающие интерес школьника к учебной деятельности.

• Способ раскрытия учебного материала.
• Организация работы над предметом малыми группами.
• Отношения между мотивом и целями.
• Проблемность обучения.
• Содержание обучения.

Формирование мотивов учебной деятельности

Используя одну схему, можно описать решение различных задач (5 класс):

•   Расстояние между двумя туристами, идущими навстречу друг другу, равно 36 км. Скорость одного туриста - 4 км/ч, а другого 5 км/ч. Через сколько часов они встретятся?
• Взрослому кролику дают 3 морковки в день, а крольчонку - две морковки в день. За сколько дней оба кролика съедят 30 морковок?
• Первый рабочий изготавливает 27 деталей в день, а второй – 33 детали в день. За сколько дней они изготовят 300 деталей?

Прежде чем смело к задачам идти, тему из букв ты сумей собери.

• 562 – (233+162) Е
• (612+276) – 412 У
• 713 + (87+189) О
• 682 – (364 + 282) И
• 65+431+35+ 69 Н
• 177-78 П
• 86+ 44 Р
• 314 – 204 Щ

476

99

130

989

110

167

600

36

167

Задача.

Клоун, чтобы посмешить публику, рассказал

одну историю о том, как он ходил на рыбалку.

В этой истории он все перепутал.

Найдите все ошибки, допущенные клоуном в

рассказе, и дайте правильный ответ.

«Я встал пораньше, в 4 кг утра.

Позавтракал плотно, выпил 1 км

молока. Потом отправился на озеро,

Расстояние до него немалое, 5 градусов.

Утром было прохладно, температура

всего 10 часов тепла. Поэтому

я шел быстро, со скоростью

6 метров. Пришел, закинул удочку,

не прошло и 20 сантиметров,

как я поймал первую рыбку.

Большущую – длиной 50 минут

и весом 3 км/ч.

Отличная получилась уха!»

Задача.

«Я встал пораньше, в 4 кг утра.

Позавтракал плотно, выпил 1 км

молока. Потом отправился на озеро,

Расстояние до него немалое, 5 градусов.

Утром было прохладно, температура

всего 10 часов тепла. Поэтому

я шел быстро, со скоростью

6 метров. Пришел, закинул удочку,

не прошло и 20 сантиметров,

как я поймал первую рыбку.

Большущую – длиной 50 минут

и весом 3 км/ч.

Отличная получилась уха!»

ч

литр

километров

градусов

км/ч

минут

сантиметров

кг

Вычислите, укажите правильный ответ

84 + 26 +44 + 116

300

320

290

100

180

330

280

150

270

260

310

400

Проверь правильность выполнения действий. Отметь неправильные решения, исправь их:

+

+

+

+

+

Проверь, все ли неравенства верные. Исправь ошибки :

Последнее неравенство надо оценить, не выполняя вычислений

12

Проверь, правильно ли решены уравнения.

Исправь ошибки, если они есть.

2.

Ошибка(3)

Укажи, какой способ решения проще:

или

или

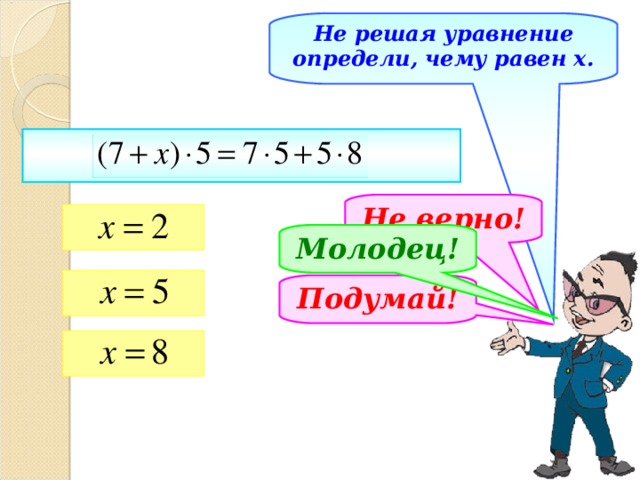
Не решая уравнение определи, чему равен х.

Не верно!

Молодец!

Подумай!

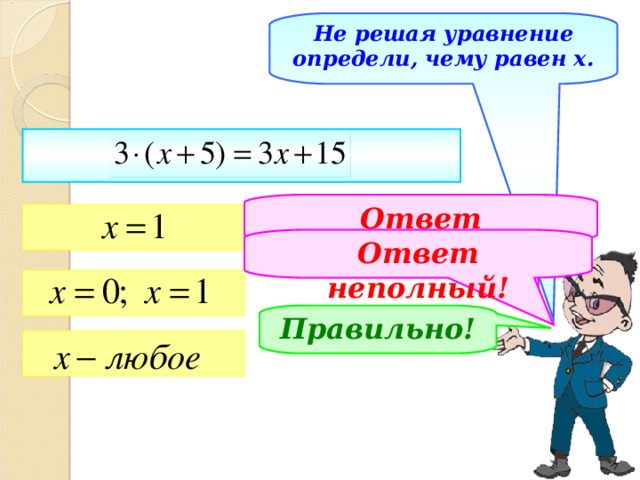
Не решая уравнение определи, чему равен х.

Ответ неполный!

Ответ неполный!

Правильно!

16

5

3

8

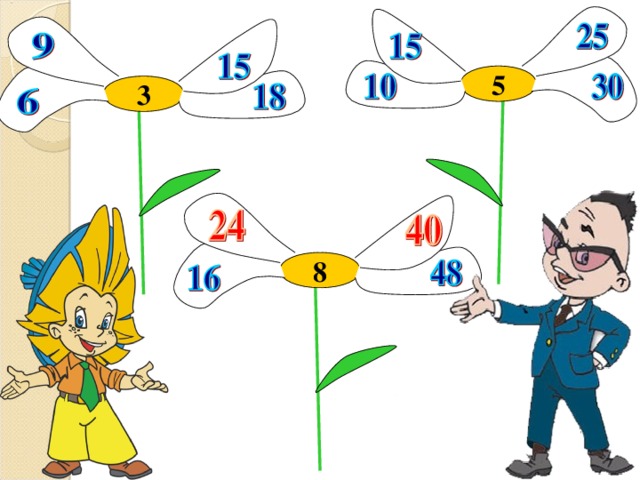
Определить закономерность образования чисел и заполнить пустые места.

17

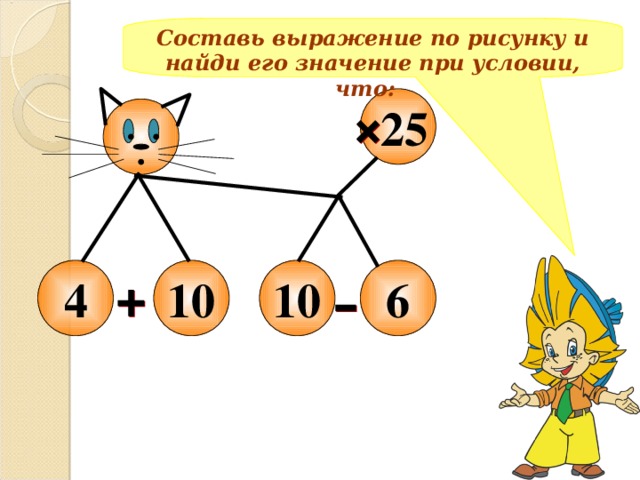
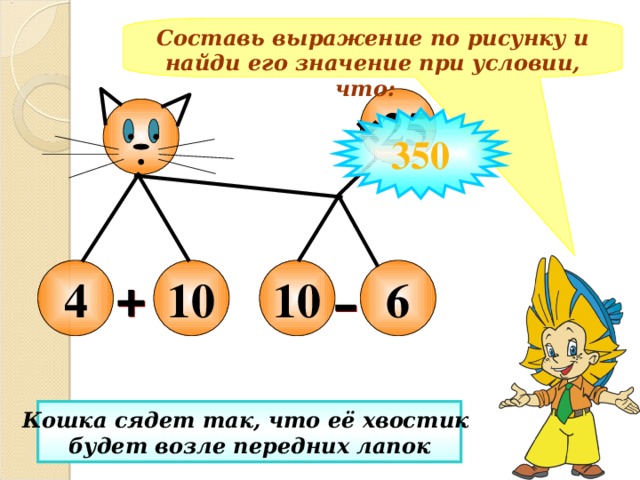
Составь выражение по рисунку и найди его значение при условии, что:

25

10

10

4

6

Составь выражение по рисунку и найди его значение при условии, что:

25

350

6

10

10

4

Кошка сядет так, что её хвостик

будет возле передних лапок

Задачка для тех, кто любит животных

Ещё в XVII столетии монахи августинского

монастыря святого Бернара в Швейцарских Альпах разводили огромных сторожевых собак.Эти собаки

прославили себя и своих хозяев тем, что во время

снежных бурь они находили и спасали заблудившихся, замерзающих, обессилевших путников. Один только легендарный пёс Барри, живший в монастыре в начале XIX века, за 10 лет

спас от верной смерти 40 человек. Определить породу этой собаки ты сможешь, если выполнишь задание…

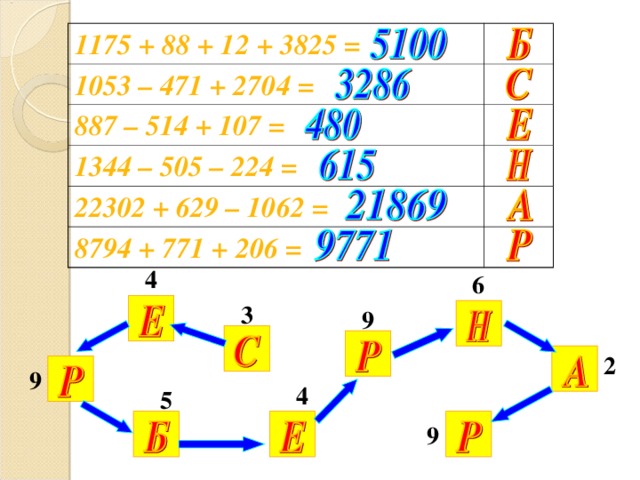
1175 + 88 + 12 + 3825 =

1053 – 471 + 2704 =

887 – 514 + 107 =

1344 – 505 – 224 =

22302 + 629 – 1062 =

8794 + 771 + 206 =

Найди значения выражений и первую цифру

получившегося числа замени соответствующей

буквой, а эти буквы запиши в «окошечки»

лабиринта.

Вычисление примеров на доскеи в тетрадях

1175 + 88 + 12 + 3825 =

1053 – 471 + 2704 =

887 – 514 + 107 =

1344 – 505 – 224 =

22302 + 629 – 1062 =

8794 + 771 + 206 =

4

6

3

9

Вычисление примеров на доскеи в тетрадях

2

9

4

5

9

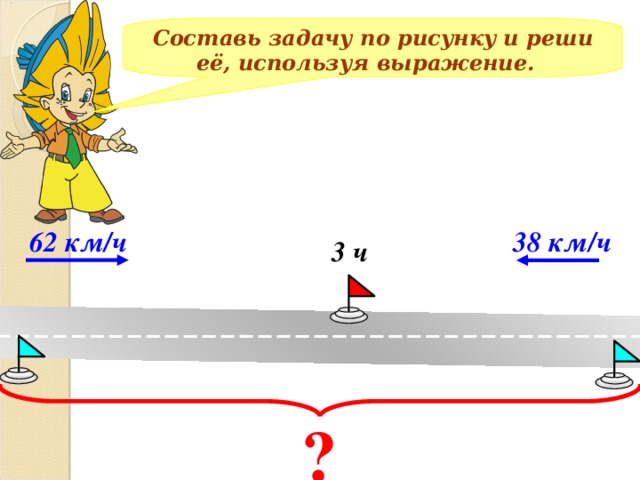
Составь задачу по рисунку и реши её, используя выражение.

38 км/ч

62 км/ч

3 ч

?

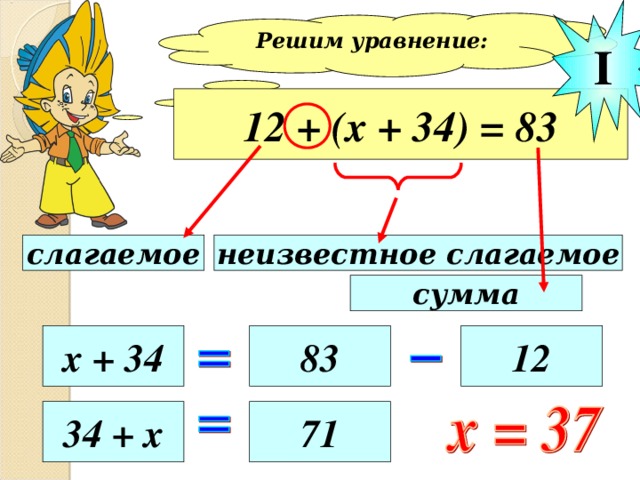
Решите уравнение :

Ключ к этому уравнению

х – 2 = 3 .

х – 1 34 = 68.

Очевидно, что х = 5,

х = 68 + 134,

поэтому х находим так :

х = 202.

Ответ: 202.

х = 3 + 2.

I

Решим уравнение:

12 + (х + 34) = 83

неизвестное слагаемое

слагаемое

сумма

х + 34

83

12

34 + х

71

Реши уравнения. Вместо букв впиши числа, которые являются корнями уравнений, записанных по вертикали, и по горизонтали.

28

32

7

47

Заполни клеточки квадрата так, чтобы в каждой строчке, столбике и по диагонали были одинаковые суммы чисел.

477

315

261

45

Составление примеров, решение – на доске и в тетрадях

Вместо звёздочек поставь цифры, чтобы получилось верное равенство

Кроссворд

По горизонтали:

2. 4. 2 6. 10. 11. . 12. 14.

По вертикали:

1. . 3. 5. 7. 8. 9. 14.

А

Д

Рисунки Савченко Е.М.

А

ЗА

Д

ЧА

ЙНИК

31

Й

Т=Й

,

C

,

,

е

Я=А

А

ЛОБ

КО

ОК

С

Т

КИ

М

В

Е

Ч

Я

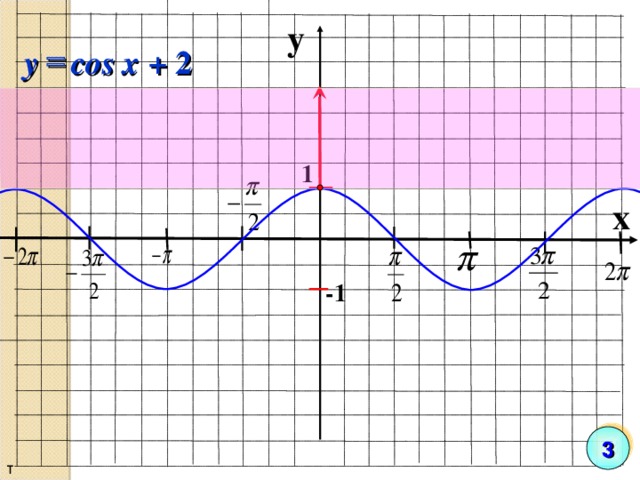
y



cos

+ 2

x

y

1

x

-1

3

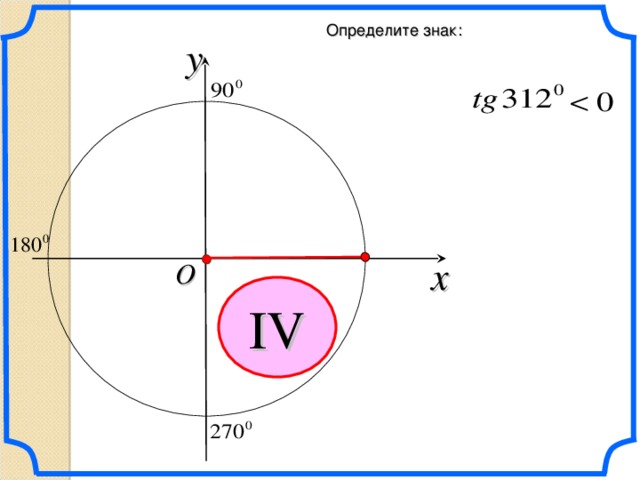
Определите знак:

y

x

O

IV

\

34

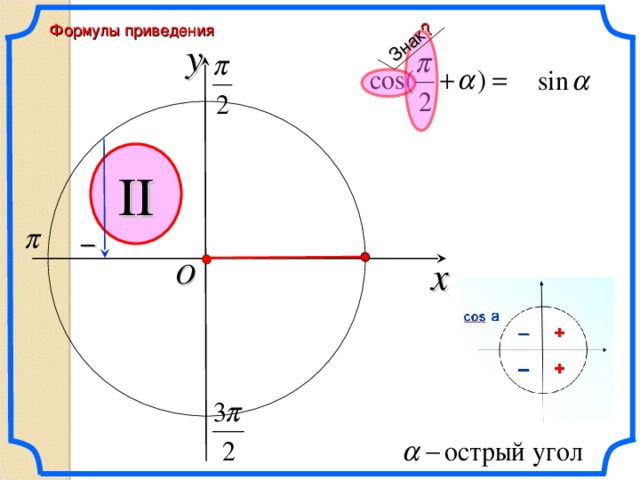
Знак ?

Формулы приведения

y

II

–

x

O

\

35

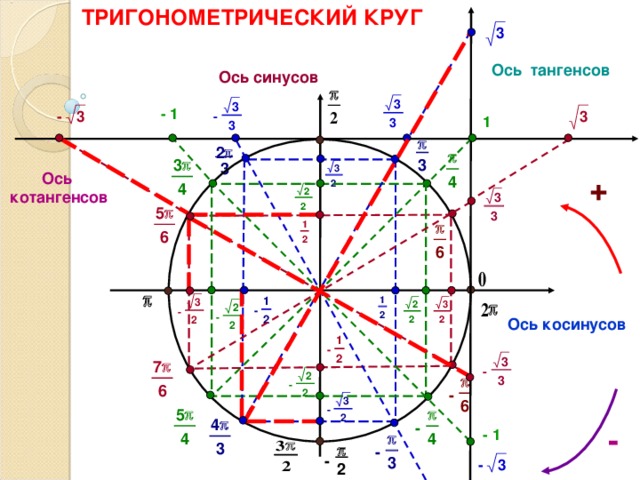
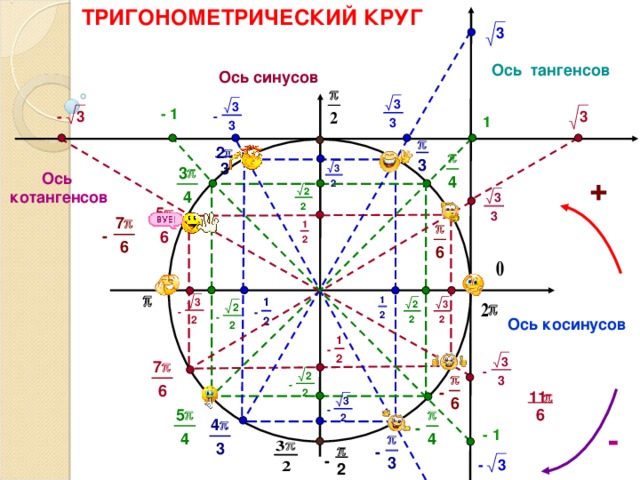
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ

3

Ось тангенсов

Ось синусов

3

3

- 1

-

3

3

-

1

3

3





2





3

3

3

3

Ось котангенсов

+

4

2

4

2

3

2



5

3



1

6

2

6

1

1

3

2

3

2

-

-

2

-

Ось косинусов

2

2

2

2

2

1

-

2

3



7

-

2



3

-

6

-

2

3

6

-





5

2



4

-

-

- 1



4

4

3



-

-

3

-

3

2

ТРИГОНОМЕТРИЧЕСКИЙ КРУГ

3

Ось тангенсов

Ось синусов

3

3

- 1

-

3

3

-

1

3

3





2



3

3



3

3

+

Ось котангенсов

4

2

2

4

3

2



5

3



7



1

-

6

2

6

6

1

1

3

2

3

2

-

-

2

-

Ось косинусов

2

2

2

2

2

1

-

2

3



7

-



2

3

-

6

-

2



11

6

3

-





6

5

2



4

-

-

- 1



4

4

3



-

-

3

-

3

2

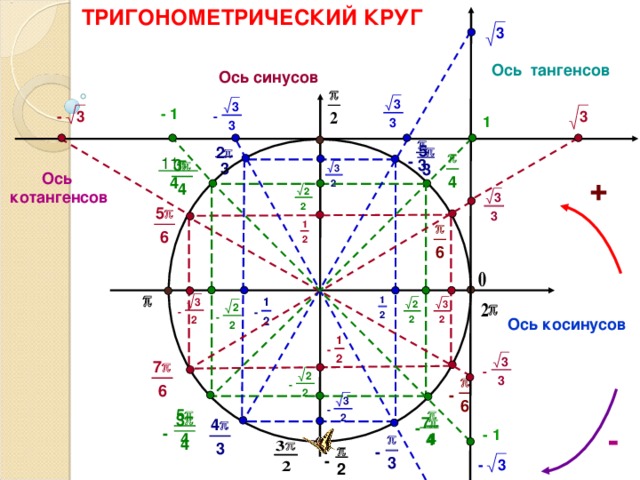
ТРИГОНОМЕТРИЧЕСКИЙ КРУГ

3

Ось тангенсов

Ось синусов

3

3

- 1

3

-

3

-

1

3

3





5



2



-



11



3

3

3

3

3

+

Ось котангенсов

4

4

2

4

2

3

2



5

3



1

6

2

6

1

1

3

3

2

2

-

-

2

-

Ось косинусов

2

2

2

2

2

1

-

2

3



7

-

2



3

-

6

-

2

3

6

-





5



3

2



7



4

-

-

-

- 1



4

4

4

4

3



-

-

3

3

-

2

На уроках также можно использовать приемы, которые значительно повышают мотивацию обучения:

• Связь изучаемого с жизнью. Зрительные ассоциации.
• Связь изучаемого с жизнью.
• Зрительные ассоциации.

• Экскурсы в историю.

• Поиск дополнительной информации с помощью библиографических справочников, словарей, энциклопедий, Интернета. Проведение уроков – практикумов на компьютере. Использование сравнений, логические тесты. Привлечение занимательных приемов, парадоксов, интеллектуальные разминки, логические задания, ребусы, математические квадраты, кроссворды. Использование игровых ситуаций (дидактические игры, интеллектуальные игры)
• Поиск дополнительной информации с помощью библиографических справочников, словарей, энциклопедий, Интернета.
• Проведение уроков – практикумов на компьютере.
• Использование сравнений, логические тесты.
• Привлечение занимательных приемов, парадоксов, интеллектуальные разминки, логические задания, ребусы, математические квадраты, кроссворды.
• Использование игровых ситуаций (дидактические игры, интеллектуальные игры)

• Использование художественной литературы: загадки, пословицы, стихи о математических терминах или о великих математиках. Создание психологического климата
• Использование художественной литературы: загадки, пословицы, стихи о математических терминах или о великих математиках.
• Создание психологического климата

карточки – информаторы,

карточки с образцами решения

• Использование творческих домашних заданий, в т. ч. с использованием компьютера.
• Использование творческих домашних заданий, в т. ч. с использованием компьютера.

Параллелепипед

В некотором царстве, некотором государстве жил: король по имени Параллелепипед со своею королевой – Площадью. И было у них три дочери, одна краше другой. Звали их Высота, Ширина и Длина.

Однажды вышли принцессы погулять в королевском лесу, да и заблудились. Начали они кликать свою матушку, но это было бесполезно. Далеко забрели девушки. Вдруг одна из сестер Высота, сказала: “ Вы – Ширина и Длина – должны найти произведение между своим ростом, и тогда посмотрим, что из этого получится ” .

Так они и сделали. В тот же миг появилась рядом с ними их матушка – Площадь.

С тех пор люди умножают ширину на длину и получают площадь. А если площадь и на высоту умножить, то получится объём прямоугольного параллелепипеда.

Определенно... математик...

Трое пустились в путь на воздушном шаре.

Но тут опустился туман, и путешественников отнесло в неизвестную им сторону. Тогда они спустились вниз, выглянули из тумана и первый спросил у прохожего:

— Уважаемый, где мы?

Прохожий подумал немного и ответил:

— Вы - на воздушном шаре.

Но тут поднялся ветер и шар снова взмыл в воздух.

— Это, определенно, был математик! — произнес второй.

— Почему же? — удивился третий.

— Во-первых, этот человек подумал, прежде чем ответить. Во-вторых, он дал верный, и, что самое главное, совершенно бесполезный ответ!

Медведь и плюшки

Медведь с базара плюшки нес,

Но на лесной опушке

Он половину плюшки съел

И плюс ещё полплюшки.

Шёл, шёл, уселся отдохнуть

И под ку-ку кукушки

Вновь половину плюшки съел

И плюс ещё полплюшки.

Стемнело. Он ускорил шаг,

Но на крыльце избушки

Он снова пол-остатка съел

И плюс ещё полплюшки.

С пустой кошелкою, увы!

Он в дом вошёл уныло.

Хочу, чтоб мне сказали вы:

А сколько плюшек было?

ЗАГАДКИ:

• 1. Сырым не едят, а сварят - выбрасывают.
• Отгадка
• Лавровый лист
• 2. Чем кончается ВСЁ?
• Отгадка
• Буквой «Ё».
•  
• 3. Кем ты станешь в 20 лет?
• Отгадка
• Двадцатилетним человеком.
•  
• 4. Почему Робин Гуд грабил богатых?
• Отгадка
• Потому что у бедных не было денег.
•  
• 5. Что не существует, но имеет название?
• Отгадка
• НИЧЕГО

Понятие «Софизм»

Софизм – (от греческого sophisma , «мастерство, умение, хитрая выдумка, уловка») - умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Софизм основан на преднамеренном, сознательном нарушении правил логики. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок.

Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.

Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения.

Я у тебя взяла 100 рублей. Пошла в магазин и потеряла их.

Встретила подругу, взяла у нее 50 рублей. Купила 2 шоколадки по 10 рублей. У меня осталось 30 рублей. Я их отдала тебе. И осталась должна 70. И подруге 50. Итого 120 рублей. Плюс 2 шоколадки.

Итого 140 рублей!

Где 10 рублей?..

ЧЕРВЯЧОК

Червячок ползет по резинке, которая может бесконечно растягиваться и никогда не порвется.

Когда червячок находился на одном конце резинки - резинка имела длину 1 м.

Когда червячок прополз 10 см, резинка увеличилась на 1 м.

Когда червячок прополз еще 10 см, резинка увеличилась еще на 1 м.

Вопрос:

Доползет ли червячок до конца резинки? Если да, то какой длины резинка будет к тому моменту?

Известно, нобелевскую премию не вручают математикам

• Многие об этом знали, другие слышали, а некоторые только открыли это для себя, и как бы это не звучало парадоксально – всемирно известную Нобелевскую премию не вручают математикам! На эту тему ходит множество легенд и историй, какие-то из них вымысел и слухи, а некоторые может и правдивы.
• Биография частной и личной жизни знаменитого изобретателя динамита, очень мало содержит фактов и достоверных дат. Многие считают, что он был женат, но как говорит его биография – он был одинок до самой старости. Создав свою премию за достижения, он не упустил никого, даже литераторам и политикам ее вручают, но вот математиков почему-то обходит стороной.
• «Почему именно математики, изучающие «царицу» всех наук, не получают нобелевские лавры за свои открытия и достижения?», – этот вопрос сложный, и мнений сложилось предостаточно. Многие математики считают, что когда Альфред Нобель диктовал список наук секретарю, составляющему завещание, он назвал химию и физику, а математику забыл упомянуть, мол, само собой разумеется, что без нее не обойтись… Другие считают, что Нобель не включил в список математику, поскольку при создании динамита, он обошелся без ее помощи.
• Третьи предполагают, что все из-за неизвестного господина, который встретился ему, когда он был со своей женой Софи в театре. Этот любезный господин, пока целовал ручку его супруге, наступил известному изобретателю на ногу. После того, как господин ушел, Нобель высказал свое недовольство, а когда заинтересовался, чем этот человек занимается, его Софи и сказала: «Он профессор математики».

• Четвертые считают, что такая ерунда, как отдавленные пальцы, не могла поспособствовать такой обиде и заставить благородного человека Нобеля, так отомстить всем математикам. Они также считают, что это связано с его супругой, но в более драматичной истории. Говорят, что придя из своей лаборатории, откуда не выходил на протяжении месяца, и где проводил успешные испытания «твердого нитроглицерина», он хотел поделиться своими успехами с любимой Софи. Распахнув двери в покои, он застал супругу с профессором математики. Ему было абсолютно все равно, чем они там занимались, но этот неизвестный профессор быстро убежал. И после этой истории Софи ушла от него и вышла замуж, но не за математика, а за какого-то кавалерийского офицера. Возможно, именно с тех пор Нобель и невзлюбил математиков, хотя сама наука тут совершенно не причем.
• Многие биографы утверждают, что австрийской жены Софи и вовсе не было, а была австрийская служанка, звали которую Берта Кински. Она была секретарем, домохозяйкой и переводчицей Нобеля в одном лице. Вскоре после своего приезда она вернулась домой в Австрию и вела переписку с ученым-изобретателем до конца его жизни. Именно может быть Берта Кински уговорила Нобеля указать в завещании знаменитую «премию мира».
• А что касается математики, то действительно, у Альфреда Нобеля были неприязненные отношения со шведским профессором математики Миттаг-Леффлером, возможно именно он и стал причиной отсутствия «царицы наук» в завещании Альфреда Нобеля.

Интересные факты:

• Все планеты нашей Солнечной системы вращаются против часовой стрелки, кроме Венеры. Это единственная планета, которая вращается по часовой стрелке.
• По данным немецких исследователей, риск сердечного приступа выше в понедельник, чем в любой другой день недели.
• Из-за гравитационных эффектов, ваш вес немного меньше, когда луна находится прямо над головой.
• В возрасте шестидесяти лет, большинство людей теряют половину своих вкусовых рецепторов.
• 40 процентов прибыли McDonald's идет от продажи Happy Meals.
• Венеция построена на 118 островках соединенных 400 мостами. Она постепенно уходит под воду.
• Фокусировочные мышцы глаз двигаются около 100000 раз в день. Чтобы мышцы ног сделали то же самое нужно пройти 80 км.

• Если вы ослепнете на один глаз, вы потеряете только около одной пятой вашего поля зрения (но вы потеряете восприятие глубины.)
• Белый медведь может выглядеть неуклюжим и медленным, но во время погони на льду, он может достигать 40 км/ч.
• Наши глаза всегда одного размера от рождения, но наш нос и уши никогда не перестают расти.
• Детеныши тигровой акулы воюют друг с другом в утробе матери. Рождаются выжившие.
• 1200000 комаров могли бы полностью высосать кровь одного человека.
• Акулы могут жить до 100 лет.
• Около 75 гектаров пиццы едят только в США каждый день .
• Американские авиалинии сэкономили $40000 в 1987 году, исключив одну оливку из каждой подаваемой порции салата в первом классе.

• Вы вырастаете примерно на 8 мм каждую ночь, когда спите. Но на следующий день вы возвращаетесь к своей обычной высоте.
• Нормальный человек смеется пять раз в день.
• Моча кошек светится под черным светом.
• В среднем, человек проводит две недели в ожидании смены цвета светофора.
• Самый красивый и невероятный подарок любви - Тадж-Махал в Индии. Построенный императором Великих Моголов Шах-Джаханом как памятник жене. Он стоит как эмблема истории вечной любви. Работа над Тадж-Махалом началась в 1634 году и продолжалась в течение почти 22 лет. Трудилось 20 тысяч рабочих со всей Индии и Центральной Азии.
• Самое длинное официальное название места в мире – Taumatawhakatangihangakoauauotamateapokaiwhenuakitanatahu.
• Оно имеет 85 букв. Это название горы в Новой Зеландии высотой 305 метров.
• Кость в пять раз прочнее стали.
• 111111111 х 111111111 = 12345678987654321
• Таракан является самым быстрым животным на 6 ногах.
• 73% людей, которые покупают цветы в День Святого Валентина - мужчины, в то время как только 27% процентов – женщины.

• Язык синего кита весит больше, чем весит слон.
• Брюс Ли был настолько быстрым, что для нас специально замедляли фильм, чтобы мы могли видеть его движения. Обычно киношники делают наоборот.
• Бамбук может расти со скоростью почти метр за сутки.
• Александр Белл, изобретатель телефона, ни разу не позвонил своей жене или матери, потому что они обе были глухими.
• С Пизанской башни упало 250 человек.
• Первый университет в мире был создан в Индии в 700 до н. э. Более 10500 студентов со всего мира изучали более 60 предметов.
• Многие рыбы могут менять пол в течение их жизни. Некоторые, особенно редкие глубоководные рыбы, имеют как мужские, так и женские половые органы.

• Население мира увеличилось на 3,1 млрд. за последние 40 лет.
• Зубы слона могут весить до 9 кг.
• Самый мощный лазер в мире (Нова Лазер в Ливерморской национальной лаборатории, штат Калифорния, США) генерирует импульс энергии, равной 100.000.000.000.000 Вт мощности.
• Жирафы не умеют плавать.
• В среднем, человек имеет 100000 волос на голове. Каждый волос вырастает на 13 см с каждым годом.
• Люди имеют 46 хромосом, горох – 14, раки - 200.
• Самый тяжелый мозг человека когда-либо зарегистрированный весил 2,3 кг.
• Киви – единственная птица, которая ищет пищу с помощью обоняния.
• В среднем, человек переворачивается 25 раз во время сна.
• К 70 годам сердце человека совершает около 2,5 миллиарда сокращений.

• 2475576000 секунд - средняя продолжительность жизни. За это время мы в среднем говорим 123205750 слов, проливаем 70 литров слез.
• У белых медведей больше проблем с теплом, чем с холодом. Даже в очень холодную погоду, они быстро перегреваются, когда бегут.
• Численность кур на земле равняется численности людей.
• Более 4 млн. автомобилей в Бразилии в настоящее время работают на газохоле вместо бензина. Газохол - это топливо из сахарного тростника.
• Нормальный человек умрет от полного отсутствия сна раньше, чем от голода. Смерть настанет где-то после 10 дней без сна, в то время как при голодании - через несколько недель.
• Когда стекло разбивается, трещины двигаются со скоростью до 3000 километров в час.
• Если человека закрыть в полностью герметичной комнате, он умрет скорее от отравления диоксидом углерода, чем от недостатка кислорода .

Игры

• Отгадывание полученного числа.
• 1.  Задумайте какое-нибудь число. Прибавьте к нему 11; умножьте полученную сумму на 2; от этого произведения отнимите 20; умножьте полученную разность на 5 и от нового произведения отнимите число, в 10 раз больше задуманного вами числа.

Я отгадываю: вы получили 10. Верно?

• 2.  Задумайте число. Утрой его. Вычти из полученного 1. Полученное умножьте на 5. К полученному прибавьте 20. Разделите полученное на 15. Из полученного вычтите задуманное.

У вас получилось 1.

• 3.  Задумайте число. Умножьте его на 6. Вычтите 3. Умножьте на 2. Прибавьте 26. Вычтите удвоенное задуманное. Разделите на 10. Вычтите задуманное.

У вас получилось 2.

• 4.  Задумайте число. Утройте его. Вычтите 2. Умножьте на 5. Прибавьте 5. Разделите на 5. Прибавьте 1. Разделите на задуманное. У вас получилось 3.
• 5.  Задумайте число, удвойте его. Прибавьте 3. Умножьте на 4. Вычтите 12. Разделите на задуманное.

У вас получилось 8.

Угадывание задуманных чисел.

Предложите своим товарищам задумать любые числа. Пусть каждый прибавит к своему задуманному числу 5.

Полученную сумму пусть умножит на 3.

От произведения пусть отнимет 7.

Из полученного результата пусть вычтет ещё 8.

Листок с окончательным результатом пусть каждый отдаст вам. Глядя на листок, вы тут же говорите каждому, какое число он задумал.

(Чтобы угадать задуманное число, результат, написанный на бумажке или сказанный вам устно, разделить на 3)

Некоторые простые числа

  Вот несколько удивительных простых чисел, которые были открыты в XVIII веке.

31

331

3331

33331

333331

3333331

33333331

Удивительно , но следующее число 333333331 не является простым! Оно делится на 17 :

17 x 19607843 = 333333331.

Это интересно - Красота математики

Перемножая ряды шестерок :

6 x 7 = 42

66 x 67 = 4422

666 x 667 = 444222

6666 x 6667 = 44442222

66666 x 66667 = 4444422222

666666 x 666667 = 444444222222

6666666 x 6666667 = 44444442222222

66666666 x 66666667 = 4444444422222222

666666666 x 666666667 = 444444444222222222

Перемножая ряды девяток

9 x 9 = 81

99 x 99 = 9801

999 x 999 = 998001

9999 x 9999 = 99980001

99999 x 99999 = 9999800001

999999 x 999999 = 999998000001

9999999 x 9999999 = 99999980000001

99999999 x 99999999 = 9999999800000001

999999999 x 999999999 = 999999998000000001

Без восьмёрки

12345679 x 9 = 111111111

12345679 x 18 = 222222222

12345679 x 27 = 333333333

12345679 x 36 = 444444444

12345679 x 45 = 555555555

12345679 x 54 = 666666666

12345679 x 63 = 777777777

12345679 x 72 = 888888888

12345679 x 81 = 999999999

Счёт в уме является самым древним и простым способом вычисления. Устные вычисления дают возможность не только быстро производить расчёты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результатах вычислений, выполненных с помощью калькулятора.

Никто не знает, когда впервые появилось число и когда первобытный человек научился считать.

Но уже несколько десятков тысяч лет назад люди собирали плоды деревьев и кустарников.

Охотились на диких животных

Делали каменные ножи и топоры, наконечники

В Древнем Вавилоне записывали числа,

выдавливая значки палочкой на глиняной дощечке.

Все числа у них составлялись из сочетаний клинышков. Вертикальная чёрточка обозначала одну единицу, а угол из двух лежачих чёрточек- десять.

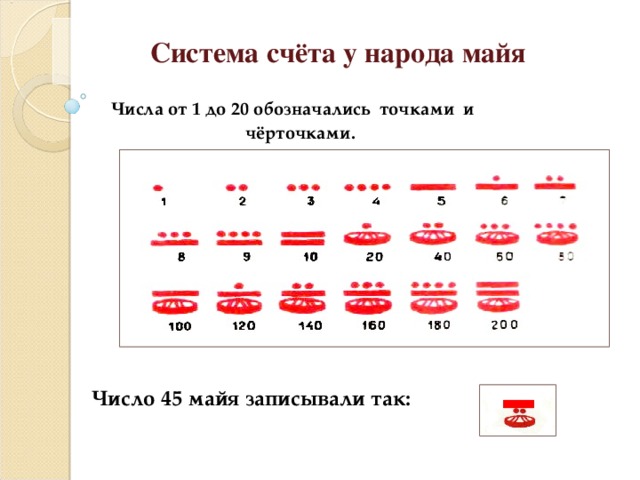
Система счёта у народа майя

Числа от 1 до 20 обозначались точками и чёрточками.

Число 45 майя записывали так:

Запись чисел в Древней Руси

Славянские цифровые знаки- буквы с титлами

В Древней Руси буква «а» обозначала число 1 Буква «б» обозначала число 2 Для обозначения чисел 10, 20,100,…, 900 использовались буквы. Для отличия букв от слов использовали знак

титло

ЗЕМЛЕДЕЛЬЦЫ

Использование «особенного» имени числительного три

• «Что я три, три раза должна повторять одно и то же!»
• « Обещанного три года ждут»,
• «За тридевять земель, в тридесятое царство».

Русский крестьянский способ умножения

В России 2-3 века назад среди крестьян некоторых губерний был распространен способ, который не требовал знание всей таблицы умножения. Надо было лишь уметь умножать и делить на 2. Этот способ получил название крестьянского (существует мнение, что он берет начало от египетского).

Пример: умножим 47 на 35,

• - запишем числа на одной строчке, проведём между ними вертикальную черту;
• - левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);
• - деление заканчивается, когда слева появится единица;
• - вычёркиваем те строчки, в которых стоят слева чётные числа;
• - далее оставшиеся справа числа складываем – это результат;

Индийский способ умножения

• х 23
• 12
• 276
• Первый шаг: х 23 «2 х 3 = 6»
• 12
• … 6
• Второй шаг: х 23 « 2 х 2 + 1 х 3 = 7»
• 12
• 76
•  
• Третий шаг: х 23 «1 х 2 = 2».
• 12 пишу 2 левее цифры 7
• получаем 276.

• Некоторые опытные учителя в прошлом веке считали, что этот способ должен заменить в нашей школе общепринятый способ умножения.
• Американцам он настолько понравился, что они его даже так и назвали «Американский способ». Однако им пользовались жители Индии еще в VI в. н. э., и правильнее его назвать «индийским способом».

Египетский способ умножения

Обозначения чисел, которые использовались в древности, были более или менее пригодны для записи результата счета. А вот выполнять арифметические действия с их помощью было очень сложно, особенно это касалось действия умножения (попробуй, перемножь: ξφß*τδ).

Выход из этой ситуации нашли египтяне, поэтому способ получил название египетского. Они заменили умножение на любое число - удвоением, то есть сложением числа с самим собой.

Метод решётки

• В своей «Книге об индийском счете» выдающийся арабский математик и астроном Абу Абдалах Мухаммед Бен Мусса аль – Хорезми, живший и работавший в Багдаде, описал способ, придуманный в Древней Индии, а позже названный «методом решётки» (он же «ревность»). Этот метод даже проще, чем применяемый сегодня.

Пусть нужно умножить 25 на 63. Начертим таблицу в которой две клетки по длине и две по ширине запишем одно число по длине другое по ширине. В клетках запишем результат умножения данных цифр, на их пересечении отделим десятки и единицы диагональю. Полученные цифры сложим по диагонали, и полученный результат можно прочитать по стрелке (вниз и вправо).

Умножение чисел на 11

• 1. Умножение на 11 числа, сумма цифр которого не превышает 10.

72 х 11 = 7 (7+2) 2 = 792;

Этот метод ещё называют «Методом Ферроля»: краешки сложи, в серединку положи.

2. Умножение на 11 числа, сумма цифр которого больше 10.

• 84 х 11 = 8 (8+4) 4 = (8+1)24 = 924;

3. Умножение на 11 по системе счёта Якова Трахтенберга

• 14326 х 11 = (1+0)(1+4), (4+3)(3+2)(2+6)6=157586.

4. Умножение на 11 по Берману

• 123 * 11 = 123 * (10 +1) = 123 * 10 + 123 * 1 = 1230 + 123 =1353

Умножение чисел на 101

Примеры:

Умножение чисел на 9, 99, 999

• К первому множителю приписать столько нулей, сколько девяток во втором множителе, и из результата вычесть первый множитель

• 1) 286 9 = 2860 – 286 = 2574;
• 2) 23 99 = 2300 – 23 = 2277;
• 3) 18 999 = 18000 – 18 = 17982.

Умножение чисел на 5 и 50

Имеем: 5 = 10 : 2, 50 = 100 : 2

Вывод:

• 1) Чтобы умножить число на 5, можно его разделить пополам, потом умножить на 10.
• 2) При умножении на 50 надо число разделить на 2 и умножить на 100.

Пример: 7,4 ∙ 5 = 7,4 : 2 ∙ 10 = 3,7 ∙ 10 = 37

• 224 ∙ 5 =224 : 2 ∙ 10 = 1120
• 36 ∙ 50 =36 : 2 ∙ 100 = 1800
• 426 ∙ 50 = 426 : 2 ∙ 100 = 21300

Умножение чисел на 25 и 250

Имеем: 25 = 100 : 4

250 = 1000 : 4

Вывод: чтобы устно умножить число на 25 или 250, надо его разделить на 4, а затем полученное частное умножить на 100 или 1000.

Примеры: 224 ∙ 25 =224 : 4 ∙ 100 = 5600

• 44 ∙ 25 =44 : 4 ∙ 100 = 1100
• 168 ∙ 250 =168 : 4 ∙ 1000 = 42000
• 72 ∙ 250 =72 : 4 ∙ 1000 = 18000

Умножение чисел на 125

Имеем:

Примеры:

Умножение чисел на 15

Имеем:

• Имеем:

Примеры:

Имеем:

Пример:

• 2

Возведение в квадрат двузначного числа, оканчивающегося на 5

Имеем: пусть число десятков х

тогда все число 10х + 5

(10х + 5)² = 100х² + 100х + 25 =

= 100х ∙ (х + 1) + 25

Вывод: чтобы возвести в квадрат двузначное число, последняя цифра которого 5, надо умножить число десятков на число, большее на единицу, к произведению приписать 25.

Примеры: 85² =7225 (т.к. 8 ∙ 9 = 72)

• 45² = 2025 (т. к. 4 ∙ 5 = 20)

«Интересные и быстрые способы и приемы вычислений»

Признаки делимости.

Эти

признаки нам

хорошо

знакомы.

• Признак делимости на 2;
• Признак делимости на 3 и на 9;
• Признак делимости на 5;
• Признак делимости на 10,100 и 1000.

Признаки делимости.

• Признак делимости на 4;
• Признак делимости на 8;
• Признак делимости на 6;
• Признак делимости на 25;
• Признак делимости на 11;
• Признак делимости на 7;
• Признак делимости на 19.

Существуют признаки делимости и на другие числа, например…

Признаки делимости.

• Число делится на 4, если две последние его цифры нули или образуют число, делящееся на 4. В остальных случаях число на 4 не делится.

Признак делимости на 4.

Признаки делимости.

Например:

• 31700 делится на 4, так как оканчивается двумя нулями;
• 215634 не делится на 4, так как последние две цифры дают число 34, не делящееся на 4;
• 16628 делится на 4, так как две последние цифры дают число 28, делящееся на 4.

Признаки делимости.

• Число делится на 8, если три последних цифры его нули или образуют число, делящееся на 8. В остальных случаях - не делится.

Признак делимости на 8.

Признаки делимости.

Например:

• 120000 делится на 8 (три нуля в конце);
• 170004 не делится на 8 (три последние цифры дают число 4, не делящееся на 8);
• 111120 делится на 8 (три последние цифры дают число 120, делящееся на 8).

Признаки делимости.

• На 8 делятся только четные натуральные числа, у которых делится на число 8, образованное двумя последними цифрами, если цифра сотен четная или равна 0.Если цифра не четная, то на восемь должно делиться число, образованное двумя последними цифрами, плюс (минус) четыре.

Признак делимости на 8.

Признаки делимости.

Например:

• 31656 делится на 8, т.к. 56 делится на 8, цифра сотен 6 четная;
• 97552 делится на 8, т.к. 52+4=56, а 56 делится на 8, цифра сотен 5 нечетная;
• 7016 делится на 8, т.к. 16 делится на 8, цифра сотен 0;
• 3844 не делится на 8, т.к. 44 не делится на 8, цифра сотен 8 четная;
• 2524 не делится на 8, т.к. 28=24+4 не делится на 8, цифра сотен 5 нечетная;
• 4398 не делится на 8, т.к. 98-4=94 не делится на 8, цифра сотен 3 нечетная.

Признаки делимости.

• Число делится на 6, если оно делится одновременно на 2 и на 3. В противном случае - не делится.

Признак делимости на 6.

Признаки делимости.

Например:

• 126 делится на 6, так как оно делится и на 2, и на 3.

Признаки делимости.

• На 25 делятся числа, две последние цифры которых нули или образуют число, делящееся на 25 (т.е. числа, оканчивающиеся на 00, 25, 50 или 75). Другие не делятся.

Признак делимости на 25.

Признаки делимости.

Например:

• 7150 делится на 25 (оканчивается на 50).
• 4855 не делится на 25 (оканчивается на 55).

Признаки делимости.

• На 11 делятся только те числа, у которых сумма цифр, занимающих нечетные места, либо равна сумме цифр, занимающих четные места, либо отличается от неё на число, делящееся на 11.

Признак делимости на 11.

Признаки делимости.

Например:

• Число 103785 делится на 11, так как сумма цифр, занимающих нечетные места, 1+3+8=12 равна сумме цифр, занимающих четные места 0+7+5=12.
• Число 9163627 делится на 11, так как сумма цифр, занимающих нечетные места, есть 9+6+6+7=28,а сумма цифр, занимающих четные места, есть 1+3+2=6; разность между числами 28 и 6 есть 22, а это число делится на 11.
• Число 461025 не делится на 11, так как числа 4+1+2=7 и 6+0+5=11 не равны друг другу, а их разность 11-7=4 на 11 не делится.

Признаки делимости.

• Зачеркни цифру единиц, удвой её и отними от оставшегося числа. Если эта разность делится на 7, то и первоначальное число делится на 7.

Признак делимости на 7.

Признаки делимости.

• Зачеркни последнюю цифру, удвой её, прибавь к оставшемуся числу, проверяй да или нет.

Признак делимости на 19.

Некоторые способы быстрых вычислений.

• При умножении таких чисел необходимо число десятков любого множителя умножить на число, которое больше на 1, затем перемножить отдельно единицы этих чисел и, наконец, к первому результату справа приписать второй.

Умножение чисел, у которых число десятков одинаково, а сумма единиц равна 10.

Некоторые способы быстрых вычислений.

Например:

• 13х17=221

а)1х(1+1)=2, пишем 2

б)3х7=21 приписываем справа 21

• 204х206=42024

а)20х(20+1)=420, пишем 420

б)6х4=24, приписываем справа 24.

Спираль?

Подводя итоги…

Уверена, что мною рассмотрена небольшая часть известных в мире математики методов и приемов вычислений, методов мотивации учащихся к учебной деятельности, которые можно назвать не только интересными, но и красивыми…

Впереди у меня интереснейшее путешествие по стране знаний.

Основные условия, при которых возникает и развивается интерес к учению.

1.Развитию мотивации учебной деятельности, любви к изучаемому предмету и к самому процессу умственного труда способствует такая организация обучения, при которой ученик действует активно, вовлекается в процесс самостоятельного поиска и "открытия" новых знаний, решает вопросы проблемного характера.

2. Учебный труд , как и всякий другой, интересен тогда , когда он разнообразен. Однообразная информация и однообразные способы действий очень быстро вызывают скуку.

3. Для появления интереса к изучаемому предмету необходимо понимание нужности, важности, целесообразности изучения данного предмета в целом и отдельных его разделов.

4. Чем больше новый материал связан с усвоенными ранее знаниями , тем он интереснее для учащихся. Связь изучаемого с интересами, уже существовавшими у школьников ранее, также способствует возникновению интереса к новому материалу.

5. Ни слишком лёгкий, ни слишком трудный материал не вызывает интереса. Обучение должно быть трудным, но посильным.

6. Чем чаще проверяется и оценивается работа школьника , тем интереснее ему работать.

7. Яркость, эмоциональность учебного материала, взволнованность самого учителя с огромной силой воздействуют на школьника, на его отношение к предмету.

И в заключение…

«Кто с детских лет занимается математикой, тот развивает внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство в достижении цели».

А. Маркушевич