
Муниципальное автономное общеобразовательное учреждение
«Школа № 17 города Белогорск»
11 класс
Учитель: Иванова Т.В.
1.
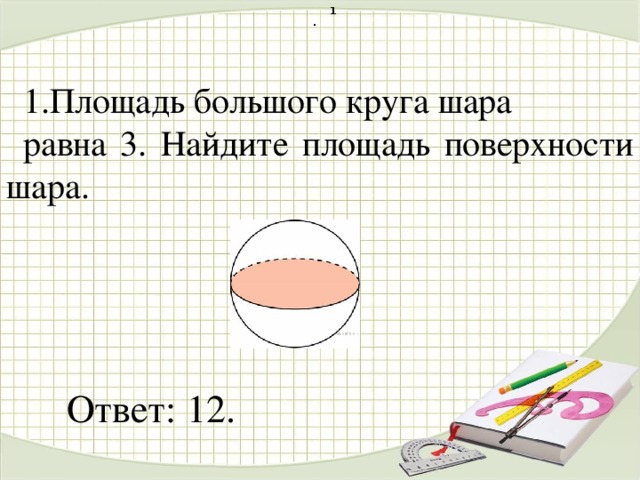
1.Площадь большого круга шара
равна 3. Найдите площадь поверхности шара.
Ответ: 12.
2
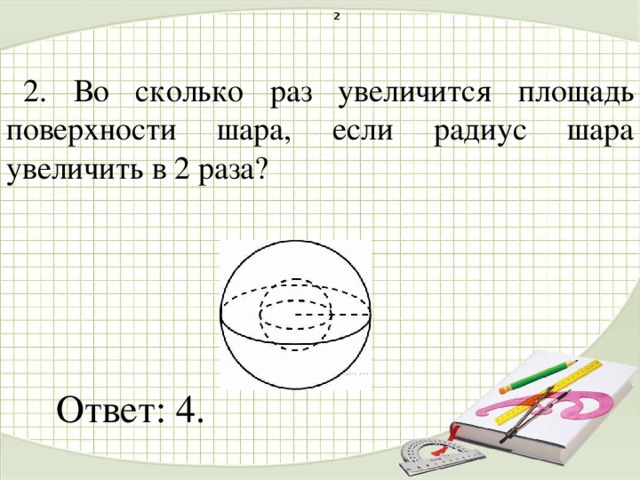
2. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Ответ: 4.

3. Во сколько раз увеличится объем шара,
если его радиус увеличить в три раза?
Ответ: 27.

4. Радиусы трех шаров равны 6, 8 и 10.
Найдите радиус шара,
объем которого равен сумме их объемов.
Ответ: 12.
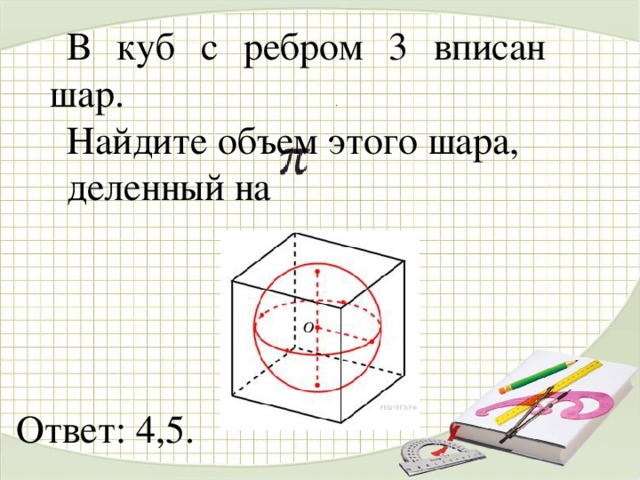
В куб с ребром 3 вписан шар.
Найдите объем этого шара,
деленный на
.
Ответ: 4,5.
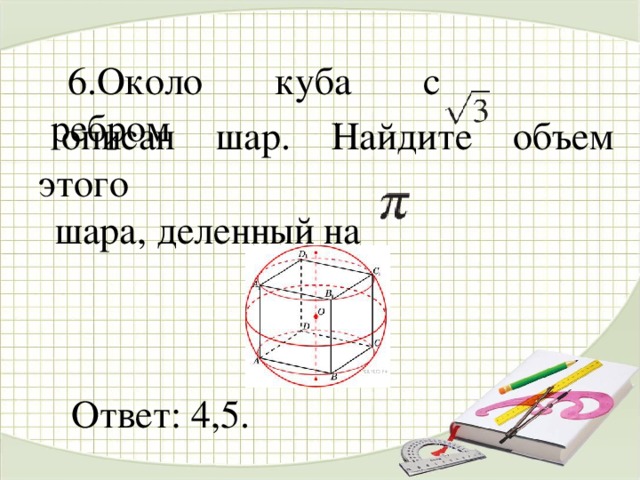
6.Около куба с ребром
.
описан шар. Найдите объем этого
шара, деленный на
Ответ: 4,5.

7.Объем одного шара в 27 раз больше
объема второго. Во сколько раз
площадь поверхности первого
шара больше площади поверхности
второго?
Ответ: 9.
8.Радиусы двух шаров равны 6, 8.
Найдите радиус шара, площадь поверхности
которого равна сумме площадей их поверхностей.
Ответ: 10.

9. Объем шара равен 288
.
. Найдите площадь его поверхности,
деленную на
Ответ: 144.

10.Вершина куба
.
со стороной 1,6 является центром
сферы, проходящей через точку
Найдите площадь части сферы,
содержащейся внутри куба.
В ответе запишите величину

Решение.
Так как одна из вершин куба является центром сферы с радиусом,
меньшим либо равным стороне куба,
в кубе содержится 1/8 часть сферы и, соответственно,
1/8 ее поверхности, равная
.
Ответ: 1,28.

.
11. Середина ребра куба со
стороной 1,9 является центром
шара радиуса 0,95. Найдите
площадь части поверхности
шара, лежащей внутри куба.
В ответе запишите

Решение.
Так как середина ребер куба является
центром сферы, диаметр которой равен ребру куба, в кубе содержится 1/4 сферы и, соответственно, 1/4 ее поверхности.
Ответ: 0,9025.

12. Конус вписан в шар.
Радиус основания конуса
равен радиусу шара.
Объем конуса равен 6.
Найдите объем шара.
Ответ: 24.
13. Куб вписан в шар радиуса
Найдите объем куба.
Ответ: 8.
14. Шар, объём которого равен 6π,
вписан в куб.
Найдите объём куба.
Ответ:36.

15. Даны два шара. Диаметр первого
шара в 8 раз больше диаметра
второго. Во сколько раз площадь
поверхности первого шара больше
площади поверхности второго?
Ответ: 64.


































