Презентация ориентирована на учащихся девятого класса. Использование данной разработки на уроке позволит школьникам подробно разобраться во всех тонкостях темы, подготовиться к решению экзаменационных заданий. В целях укрепления собственных знаний школьники смогут дополнительно изучить мультимедийный материал на персональном компьютере.
Презентацию отличает четкая структура и яркое оформление. Текстовой материал, подлежащий запоминанию, выделен синим цветом. Дополнительное выделение ключевых моментов с помощью анимационных эффектов привлечет зрителей, обеспечит прочное запоминание теории. Разнообразие тренировочных заданий поможет выработать навык решения тематических заданий, будет способствовать развитию умений анализировать, сравнивать. Присутствие дополнительных иллюстраций не позволит никому заскучать на уроке, сделает занятие более интересным.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация решение систем неравенств 9 класс
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация решение систем неравенств 9 класс»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1630 руб.
2710 руб.
1490 руб.
2480 руб.
1720 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства





 6 2х – 4 Решение: решим каждое неравенство отдельно 5х + 1 6 2х – 4 5х 6 -1 2х 5х 5 2х х 1 х 1 3,5 х Ответ: (1; 3,5)" width="640"
6 2х – 4 Решение: решим каждое неравенство отдельно 5х + 1 6 2х – 4 5х 6 -1 2х 5х 5 2х х 1 х 1 3,5 х Ответ: (1; 3,5)" width="640"
 - 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4]" width="640"
- 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4]" width="640"
 12 + 11х 5х – 1 ≥ 0 Проверим ответы: 1) [2; +∞) 2) Нет решения" width="640"
12 + 11х 5х – 1 ≥ 0 Проверим ответы: 1) [2; +∞) 2) Нет решения" width="640"

 0 4х + 2 ≤ 6 Решим каждое неравенство системы отдельно: 1) 4х + 2 0 2) 4х + 2 ≤ 6 х - 0,5 х ≤ 1 Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5 или (-0,5; 1]" width="640"
0 4х + 2 ≤ 6 Решим каждое неравенство системы отдельно: 1) 4х + 2 0 2) 4х + 2 ≤ 6 х - 0,5 х ≤ 1 Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5 или (-0,5; 1]" width="640"
![Решите неравенства, работая в парах Решить неравенства: Проверим ответы: 1) [-1; 2] 2) (2,5; 7 ] 3) [- 1,5; - 1) 4) (-2; 1) 5) (-4; 0) -6 ≤ - 3х ≤ 3 4 ≤ 13 -2 ≤ 6х + 7 1 0,3 0](https://fsd.kopilkaurokov.ru/uploads/user_file_56d2e8eced7b9/img_user_file_56d2e8eced7b9_10.jpg)
 9/4=2,25 Полученные результаты изобразим на числовой прямой: 1 2,25 4 х Ответ: [ 4; +∞)" width="640"
9/4=2,25 Полученные результаты изобразим на числовой прямой: 1 2,25 4 х Ответ: [ 4; +∞)" width="640"
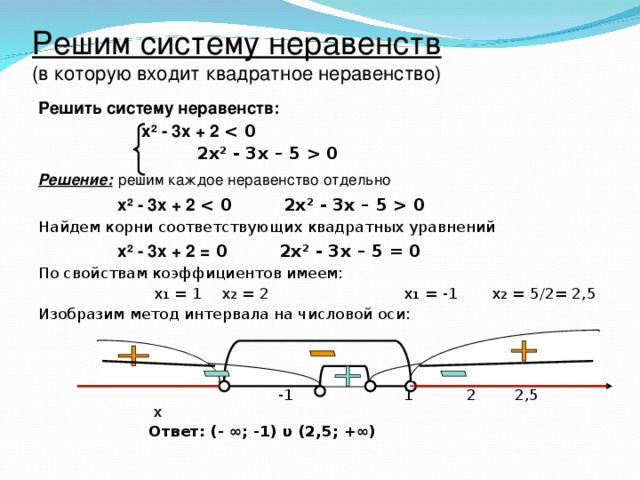 0 Решение: решим каждое неравенство отдельно х ² - 3х + 2 2х² - 3х – 5 0 Найдем корни соответствующих квадратных уравнений х ² - 3х + 2 = 0 2х² - 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (- ∞; -1) υ (2,5; +∞)" width="640"
0 Решение: решим каждое неравенство отдельно х ² - 3х + 2 2х² - 3х – 5 0 Найдем корни соответствующих квадратных уравнений х ² - 3х + 2 = 0 2х² - 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (- ∞; -1) υ (2,5; +∞)" width="640"
 0 4х – 1 ≥ 0 2) 4х² - 1 ≤ 0 х² 1 3х² - 2х – 1 х² - х – 6 0" width="640"
0 4х – 1 ≥ 0 2) 4х² - 1 ≤ 0 х² 1 3х² - 2х – 1 х² - х – 6 0" width="640"
 0 4х – 1 ≥ 3 3) 2х² - 7х + 5 2 – х ≥ 0 Проверим ответы: 1) (4; 9 ] 2) [1; 2) 3) (- ∞ ; 1 )" width="640"
0 4х – 1 ≥ 3 3) 2х² - 7х + 5 2 – х ≥ 0 Проверим ответы: 1) (4; 9 ] 2) [1; 2) 3) (- ∞ ; 1 )" width="640"
















