Презентация по алгебре "Квадратные корни"

Квадратные корни

Цели: ввести понятия квадратного корня и арифметического квадратного корня; формировать умение извлекать квадратные корни.

Ход урока

I. Организационный момент.

II. Устная работа.

– Вычислите:

а) 72;               б) ;              в) 112;                  г) ;

д) ;         е) 0,22;                 ж) ;              з) 0,62.

III. Объяснение нового материала.

1. В в е д е н и е   п о н я т и я  квадратного корня.

Сначала рассмотрим задачу о нахождении стороны квадрата по его площади.

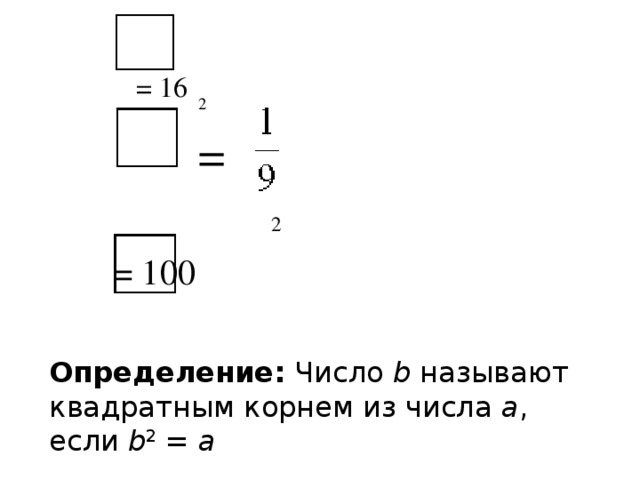
Вписать в пустые клеточки числа, чтобы равенства были верными:

2 = 16

2 =

2 = 100

После этого дать определение квадратного корня из числа.

Определение: Число b называют квадратным корнем из числа а, если b2 = а.

Выяснить, является ли число п квадратным корнем из числа т, если:

а) п = 5, т = 25;                         в) п = 0,3, т = 0,9;

б) п = –7, т = 49;                       г) п = 6, т = –36.

2. В в е д е н и е   п о н я т и я  арифметического квадратного корня.

равенство  = b означает одновременное выполнение двух условий: b2 = а и b ≥ 0.

Определить, является ли число п арифметическим квадратным корнем из числа т, если:

а) п = 8, т = 64;                         в) п = 0,2, т = 0,4;

б) п = –3, т = 9;                         г) п = 0,4, т = 0,16.

3. И с т о р и ч е с к а я   с п р а в к а.

– Обратим внимание на совпадение в терминах – квадратный корень и корень уравнения. Это совпадение не случайно. Уравнения вида х2 = а исторически были первыми сложными уравнениями, и их решения были названы корнями по метафоре, что из стороны квадрата, как из корня, вырастает сам квадрат. В дальнейшем термин «корень» стал употребляться и для произвольных уравнений.

Название «радикал» тоже связано с термином «корень»: по-латыни корень – radix (он же редис – корнеплод). Также слово «радикальный» в русском языке является синонимом слова «коренной». Происхождение же символа  связывают с написанием латинской буквы r.

4. Основное свойство арифметического квадратного корня.

.

IV. Формирование умений и навыков.

1. № 298, № 299.

2. № 300.

При вычислении обратить внимание на следующее:

Н а п р и м е р:  = 7, поскольку 72 = 49.

– При нахождении корня из дроби пока нельзя извлекать отдельно корень из числителя и из знаменателя, поскольку соответствующее свойство корней будет рассмотрено позже.

3. № 305, № 306 (а, б).

4. № 309.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Что называется квадратным корнем из числа а?

– Сколько квадратных корней может быть из числа а?

– Что такое арифметический квадратный корень из числа а?

– Имеет ли смысл запись ? Почему?

– Всегда ли верно равенство  = а?

Домашнее задание: № 301, № 304, № 306 (в, г).