Разработка содержит алгоритмы построения элементарных преобразований графиков функций, зрительную интерпритацию преобразования и примеры.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация на тему: "Элементарные преобразования графиков функций"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация на тему: "Элементарные преобразования графиков функций"»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
1570 руб.
2240 руб.
1970 руб.
2820 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

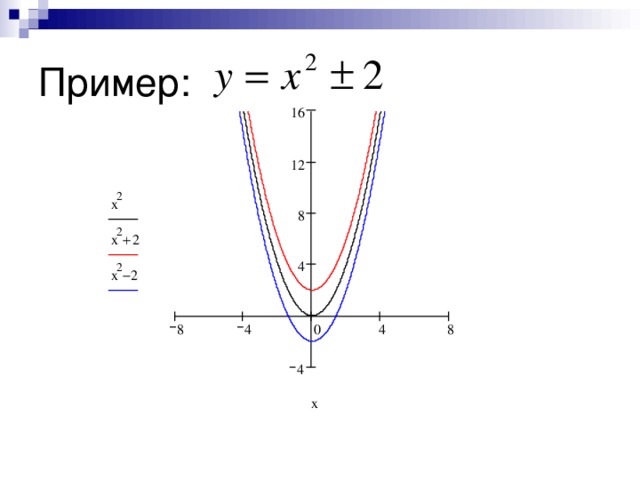
 0 График функции y = f ( x ) -a , где a – постоянное число, получается из графика y = f ( x ) смещением его вдоль оси Oy на a единиц вниз, если a 0 Y y=f(x)+a a a 0 X y=f(x) y=f(x)-a " width="640"
0 График функции y = f ( x ) -a , где a – постоянное число, получается из графика y = f ( x ) смещением его вдоль оси Oy на a единиц вниз, если a 0 Y y=f(x)+a a a 0 X y=f(x) y=f(x)-a " width="640"
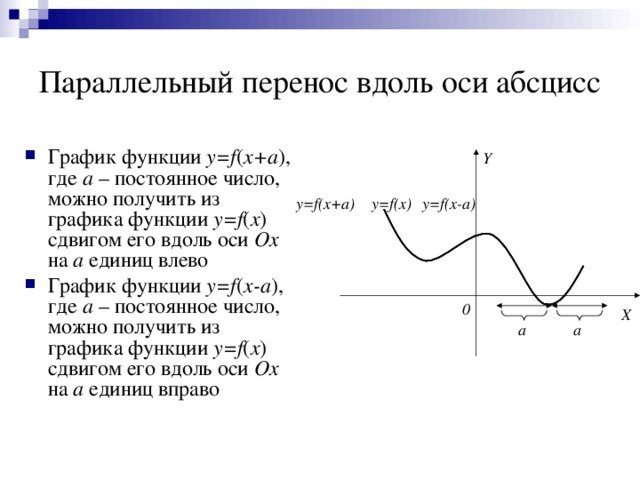



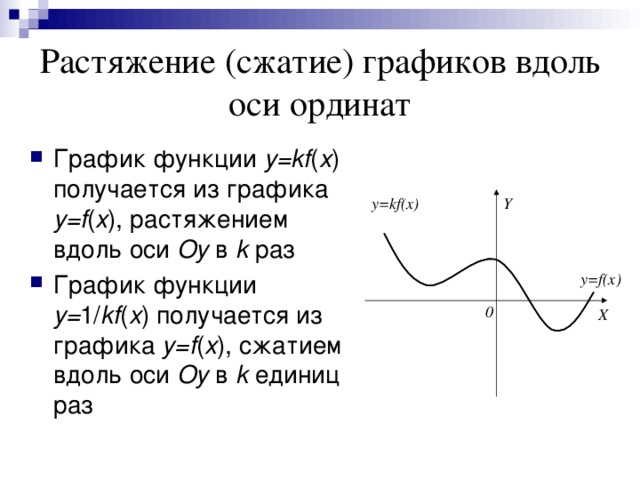
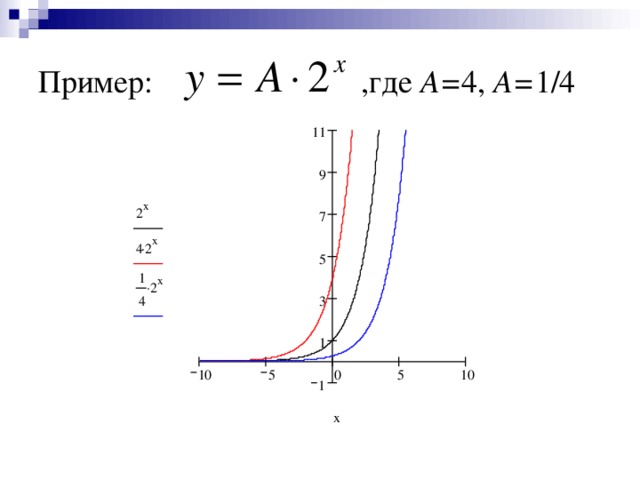
 1 или растянут в 1/ k раз, если 0 k 1 y=f(kx) Y y=f(x) 0 X " width="640"
1 или растянут в 1/ k раз, если 0 k 1 y=f(kx) Y y=f(x) 0 X " width="640"
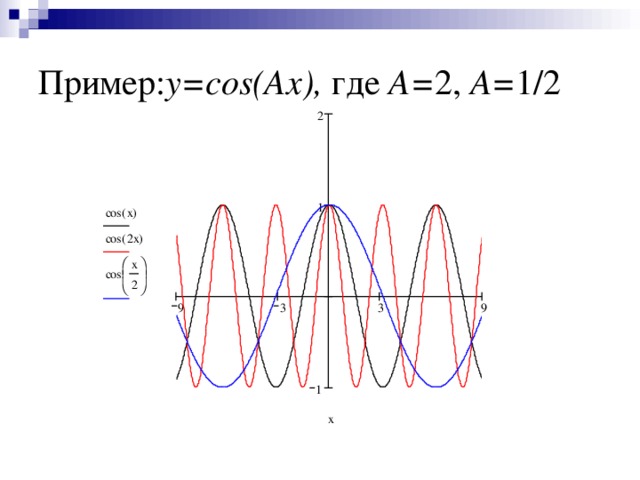
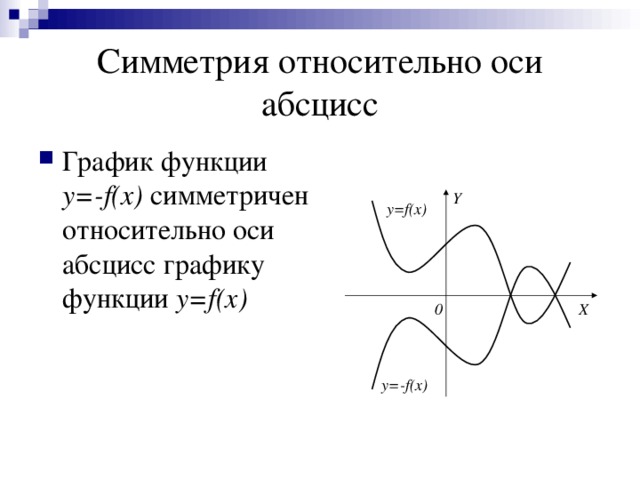
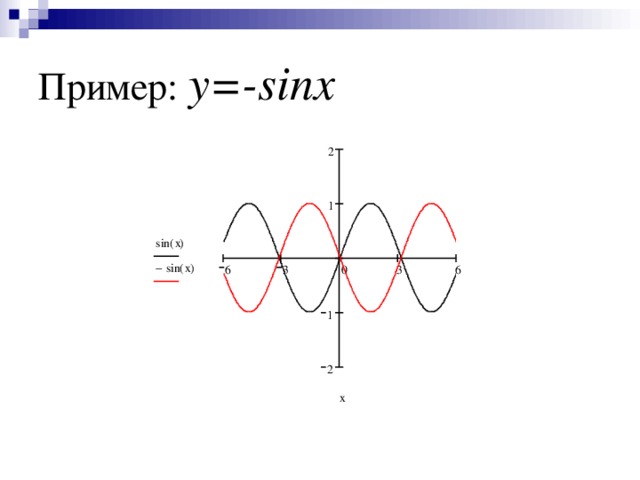
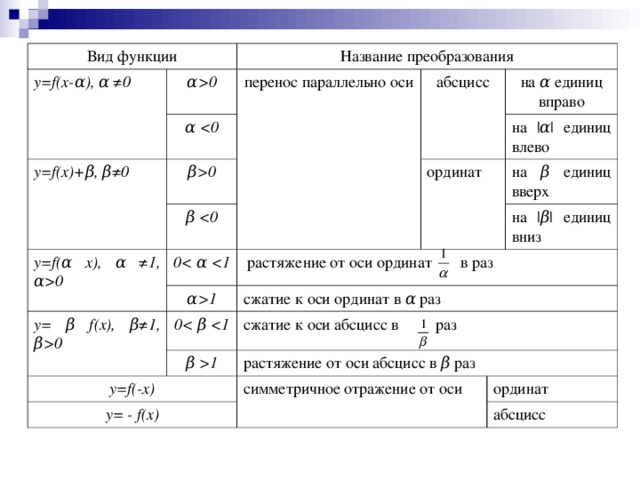 0 перенос параллельно оси α y=f(x)+β, β≠0 абсцисс β0 y=f(α x), α ≠1, α0 β ординат 0 на α единиц вправо α1 y= β f(x), β≠1, β0 растяжение от оси ординат в раз на | α | единиц влево сжатие к оси ординат в α раз 0 на β единиц вверх сжатие к оси абсцисс в раз β 1 на | β | единиц вниз y=f(-x) растяжение от оси абсцисс в β раз y= - f(x) симметричное отражение от оси ординат абсцисс " width="640"
0 перенос параллельно оси α y=f(x)+β, β≠0 абсцисс β0 y=f(α x), α ≠1, α0 β ординат 0 на α единиц вправо α1 y= β f(x), β≠1, β0 растяжение от оси ординат в раз на | α | единиц влево сжатие к оси ординат в α раз 0 на β единиц вверх сжатие к оси абсцисс в раз β 1 на | β | единиц вниз y=f(-x) растяжение от оси абсцисс в β раз y= - f(x) симметричное отражение от оси ординат абсцисс " width="640"















