дается определение площади. рассматриваются единицы площади, свойства площади, площадь прямоугольника, треугольника, параллелограмма, трапеции. доказывается теорема пифагора, и показывается ее применение при решении задач. предлагаются задачи для самостоятельной работы. проводится самостоятельная работа для закрепления материала.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация по геометрии 8 класс "Площади фигур"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация по геометрии 8 класс "Площади фигур"»
Полезное для учителя
Распродажа видеоуроков!
2220 руб.
3170 руб.
1740 руб.
2480 руб.
2000 руб.
2860 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


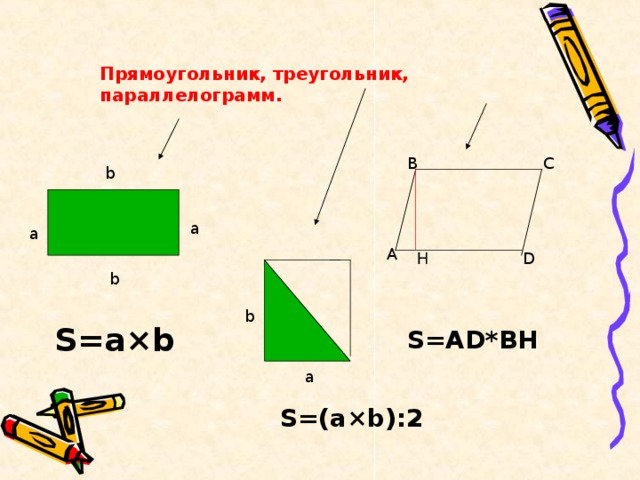



 Площади ABCD и HBCK также равны,т.е. площадь прямоугольника HBCK равна S . По теореме = S=BC*BH , а так как BC=AD, то S=AD*BH В С 1 2 А K H D" width="640"
Площади ABCD и HBCK также равны,т.е. площадь прямоугольника HBCK равна S . По теореме = S=BC*BH , а так как BC=AD, то S=AD*BH В С 1 2 А K H D" width="640"
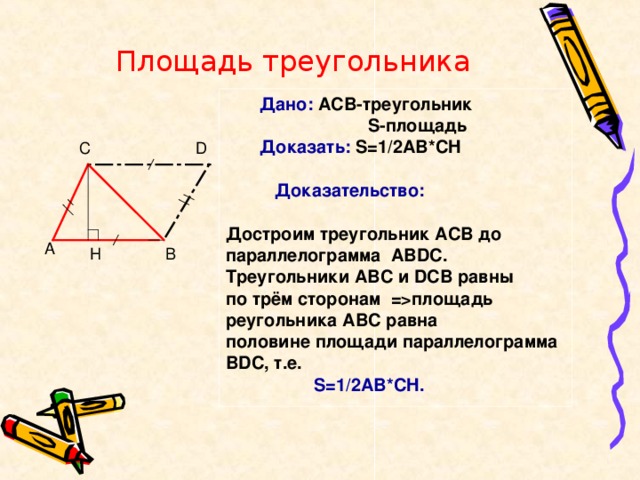 площадь реугольника АВС равна половине площади параллелограмма BDC, т.е. S=1/2AB*CH. D C A H B" width="640"
площадь реугольника АВС равна половине площади параллелограмма BDC, т.е. S=1/2AB*CH. D C A H B" width="640"
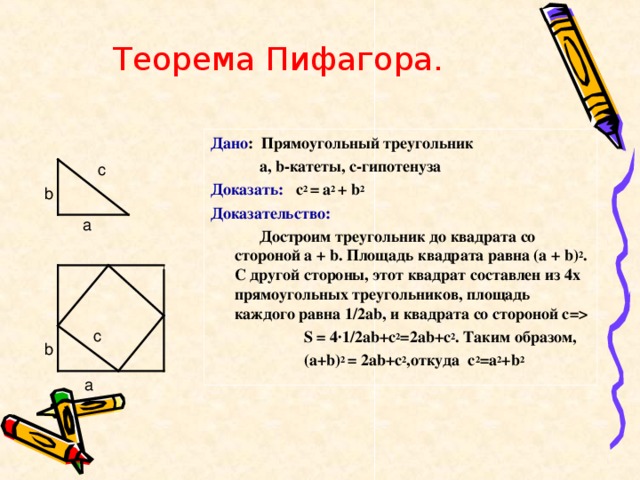 S = 4∙1/2ab+c 2 =2ab+c 2 . Таким образом, (a+b) 2 = 2ab+c 2 , откуда c 2 =a 2 +b 2 c b а c b a" width="640"
S = 4∙1/2ab+c 2 =2ab+c 2 . Таким образом, (a+b) 2 = 2ab+c 2 , откуда c 2 =a 2 +b 2 c b а c b a" width="640"

















