Первый урок алгебры в 7 классе
Что такое «алгебра»?
Вычислите устно:
-8,4-10
2,4
-18,4
-0,25
-7/8
0,6
Найдите значение выражения:
3(2х – 4) – 2(х + 3) = –2+8x
Решите уравнение:
6х-12-2х-6=-2+8х
4х-18=-2+8х
4х-8х=-2+18
-4х=16
х=16:(-4)
х=-4
Преподдобенская колокольняРизоположенского монастыря
Высота «прямоугольного» основания Преподдобенской колокольни составляет от общей высоты. Высота «колоннады» составляет 62% общей высоты, а высота шпиля равна 12,96 м. Чему равна высота Преподдобенской колокольни?
На территории Ризоположенского монастыря располагается самое высокое здание в Суздале: Преподдобенская колокольня. Ее построили в период с 1813 по -1819 годы. Ее высота достигает 72 метра! Преподдобенскую колокольню видно не только в Суздале, но и за много километров за его пределами. По легенде Преподдобенскую колокольню возвели в честь победы русских войск в Отечественной войне 1812 год.
Решите задачу:
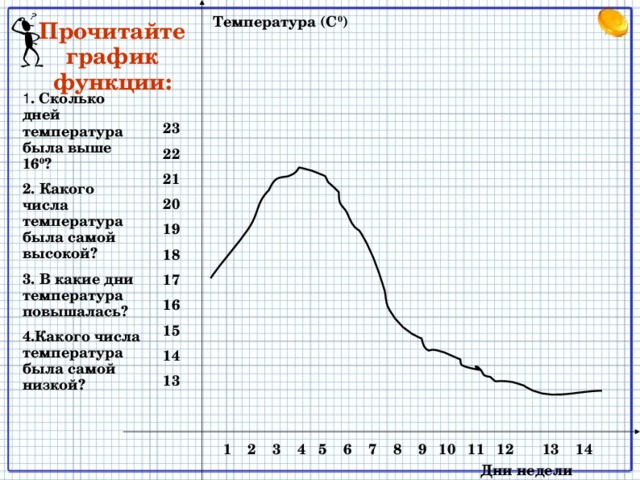
1 2 3 4 5 6 7 8 9 10 11 12 13 14
23 22 21 20 19 18 17 16 15 14 13
Дни недели
Температура (С0)
1. Сколько дней температура была выше 160?2. Какого числа температура была самой высокой?3. В какие дни температура повышалась?4.Какого числа температура была самой низкой?
Прочитайте график функции:
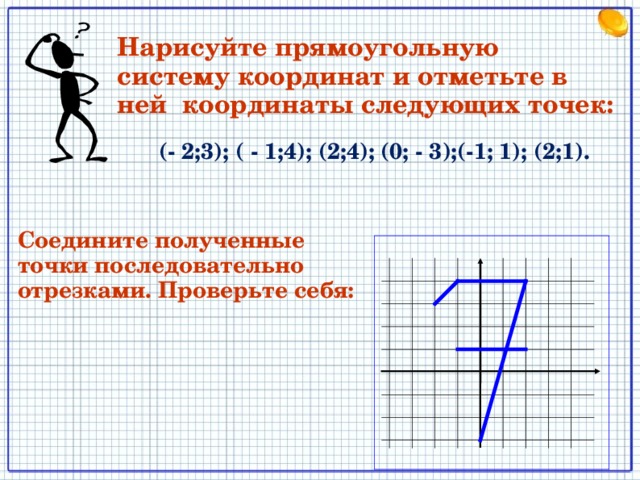
(- 2;3); ( - 1;4); (2;4); (0; - 3);(-1; 1); (2;1).
Нарисуйте прямоугольную систему координат и отметьте в ней координаты следующих точек:
Соедините полученные точки последовательно отрезками. Проверьте себя:
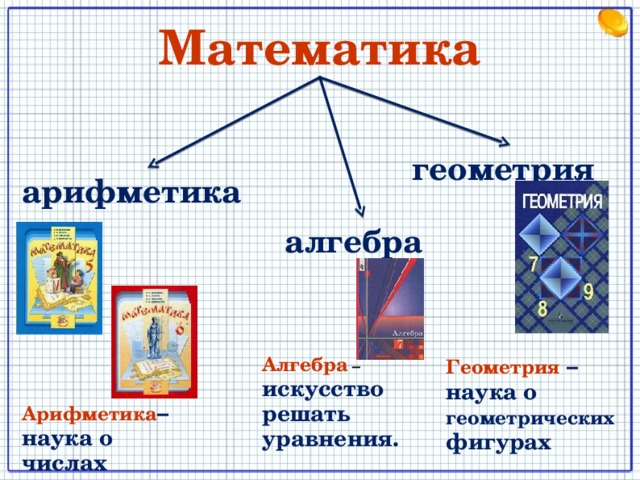
Математика
арифметика
алгебра
геометрия
Арифметика– наука о числах
Алгебра – искусство решать уравнения.
Геометрия – наука о геометрических фигурах
–это что?
Алгебра
Слово «алгебра» возникло после появления трактата хорезмского математика и астронома Мухаммеда бен Муса аль-Хорезми.
Алгебра как искусство решать уравнения зародилась очень давно в связи с потребности практики, в результате поиска общих приемов решение однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были изданы приёмы решения линейных уравнений.Математик аль-Хорезми (727-ок.850), живший в древней столице Хорезма городе Ургенч, написал в начале IX века свою книгу, которая стала родоначальником европейских учебников алгебры.
Он назвал её «Книга о восстановлении и противопоставлении» "Аль-китаб аль мухтасар фи хисаб аль-джабр ва аль-мукабала".« Восстановление» означает превращение вычитаемого ( по современному – «отрицательного» ) числа в положительное при перенесении из одной половины уравнения в другую. Так как в те времена отрицательные числа не считались настоящими, то операция аль – джебр ( алгебра) , как бы возвращающая число из небытия в бытие, казалось чудом этой науки, которую в Европе долго после этого называли «великим искусством» , рядом с «малым искусством» - арифметикой.
Уже аль-Хорезми видел характерную способность алгебры в том, что она решает задачи, рассматриваемые и в арифметике, в общем виде. Достигается это тем, что числа обозначаются буквами, которые, в зависимости от условия задачи, могут получать разные числовые значения. Поэтому алгебру часто называли общей или универсальной арифметикой.
Алгебра
Арифметика
До XVI в. изложение алгебры велось в основном словесно. Буквенные обозначения и математические знаки появились постепенно. Знаки + и – впервые встречаются у немецких алгебраистов XVI в. Несколько позже вводиться знак «х» для умножения. Знак деления (:) был введён лишь в XVII в. Современные знаки умножения в виде «*» и деление в виде «:» впервые использовал Лейбниц. Знак деления в 1684 г., а умножения - в 1698 г.
Аль-Хорезми внес неоценимый вклад в мировую науку, став основоположником алгебры. К сожалению, о жизни великого ученого, чьи труды легли в основу многих фундаментальных наук, о жизни "самого выдающегося математика своего времени, а если учесть атмосферу и обстоятельства того периода, быть может, самого выдающегося математика всех эпох" (Ж.Сартон), не сохранилось почти никаких материалов .
Успехов Вам, ребята, в изучении этой науки.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация "Первый урок алгебры" 7 класс
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация "Первый урок алгебры" 7 класс »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
1570 руб.
2240 руб.
1970 руб.
2820 руб.
1790 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства