Слайды к уроку "Логарифмическая функция" для 11-го класса.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
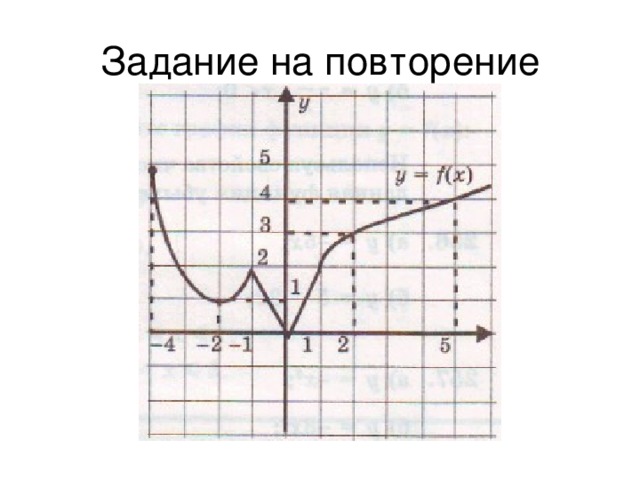
Презентация к открытому уроку "Логарифмическая функция"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация к открытому уроку "Логарифмическая функция"»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2220 руб.
3170 руб.
2000 руб.
2860 руб.
1790 руб.
2560 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства





 0, а ≠ 1 . " width="640"
0, а ≠ 1 . " width="640"



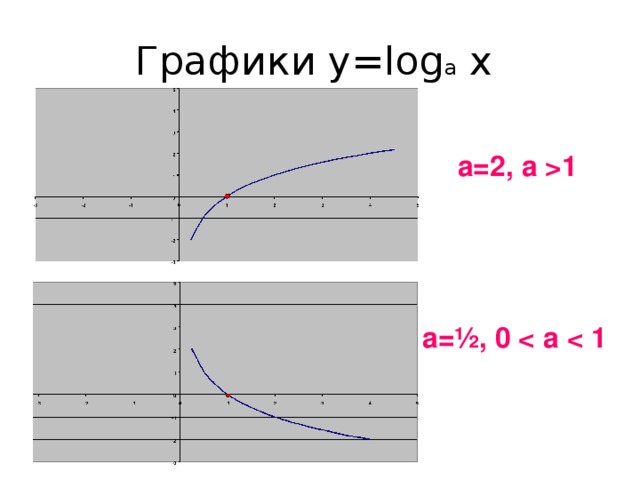 1 а=½, 0 " width="640"
1 а=½, 0 " width="640"
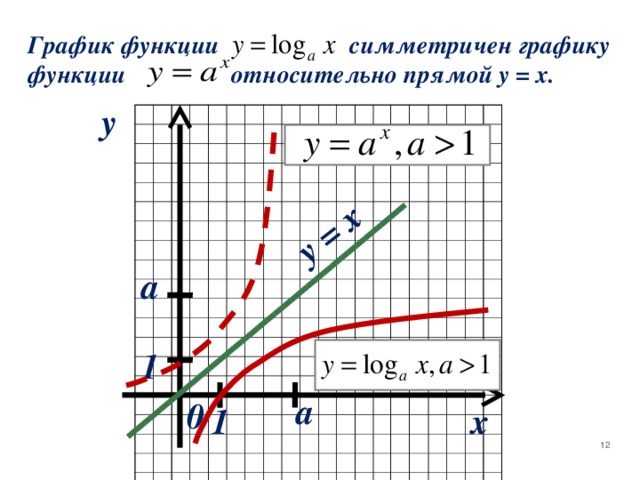
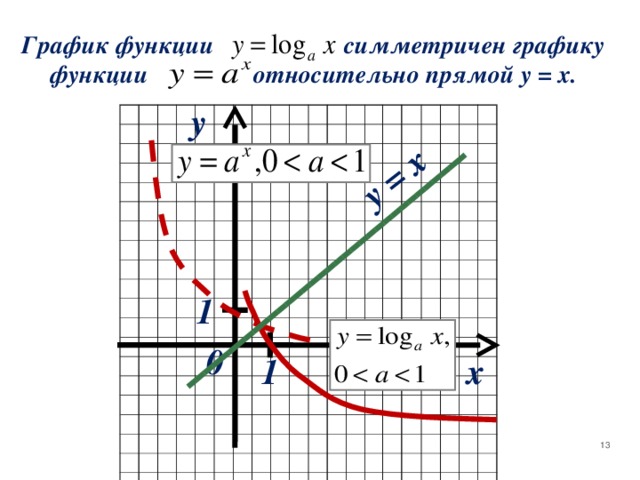
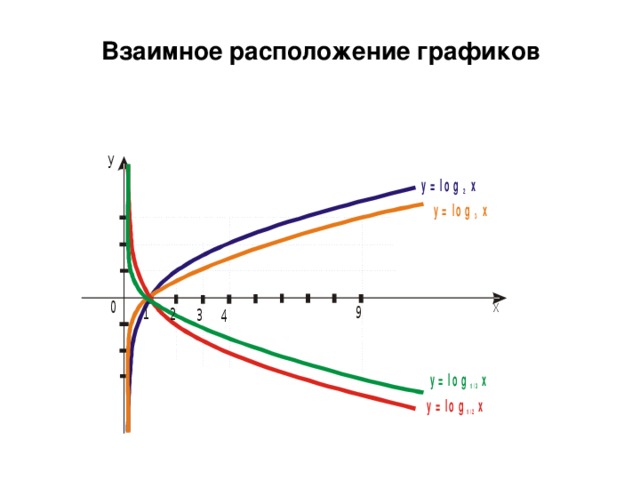
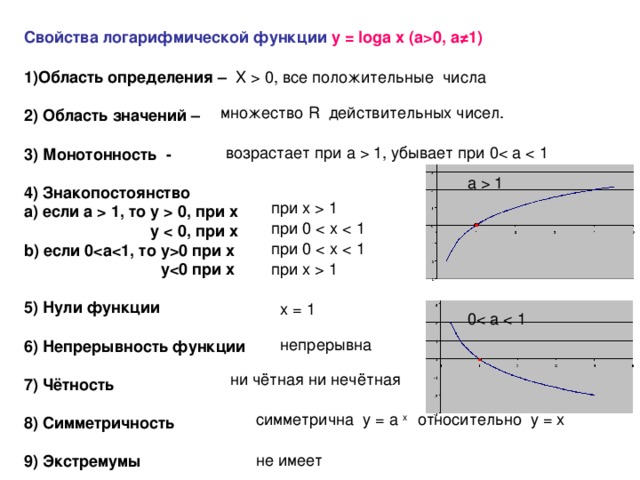 0, а ≠ 1) 1)Область определения – 2) Область значений – 3) Монотонность - 4) Знакопостоянство а) если a 1 , то y 0 , при х y при х b ) если 0 , то y0 при x y при x 5) Нули функции 6) Непрерывность функции 7) Чётность 8) Симметричность 9) Экстремумы X 0 , все положительные числа множество R действительных чисел. возрастает при a 1 , убывает при 0х a 1 при х 1 при 0 при 0 при х 1 х = 1 0х " width="640"
0, а ≠ 1) 1)Область определения – 2) Область значений – 3) Монотонность - 4) Знакопостоянство а) если a 1 , то y 0 , при х y при х b ) если 0 , то y0 при x y при x 5) Нули функции 6) Непрерывность функции 7) Чётность 8) Симметричность 9) Экстремумы X 0 , все положительные числа множество R действительных чисел. возрастает при a 1 , убывает при 0х a 1 при х 1 при 0 при 0 при х 1 х = 1 0х " width="640"
 0 0 " width="640"
0 0 " width="640"
 " width="640"
" width="640"
 3 » Комедия начинается с неравенства, бесспорно правильно. Затем следует преобразование Тоже не внушающее сомнения Большему числу соответствует больший логарифм, если функция возрастает, значит, После сокращения на Имеем 2 3. В чем ошибка этого доказательства? " width="640"
3 » Комедия начинается с неравенства, бесспорно правильно. Затем следует преобразование Тоже не внушающее сомнения Большему числу соответствует больший логарифм, если функция возрастает, значит, После сокращения на Имеем 2 3. В чем ошибка этого доказательства? " width="640"

































