Презентация для урока на тему «Квадратные уравнения»

Составить из квадратного уравнения х2 – 2х – 8 = 0 три вида неполных квадратных уравнений, ориентируясь на диагностическую таблицу.

Решить полученные уравнения.

Определить р и х2 в квадратном уравнении

х2 – рх + 15 = 0, если х1 = 3.

Найденное значение х2 укажет номер кабинета, где лежит приз, р – номер парты (если считать от окна).

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Презентация для урока на тему «Квадратные уравнения»»

Урок обобщения и систематизации знаний по теме

«Квадратные уравнения»

Выполнила Беспалова Л.И. учитель математики МБОУ «Ковылкинская вечерняя (сменная) общеобразовательная школа»

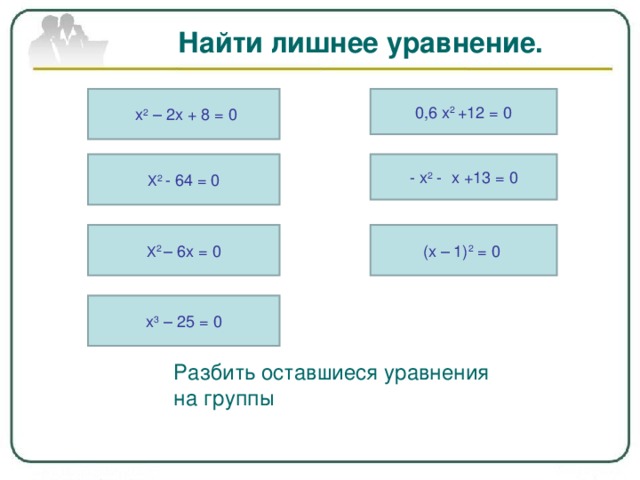
х 3 – 25 = 0

Разбить оставшиеся уравнения на группы

Найти лишнее уравнение.

х 2 – 2х + 8 = 0

0,6 х 2 +12 = 0

Х 2 - 64 = 0

- х 2 - х +13 = 0

Х 2 – 6х = 0

(х – 1) 2 = 0

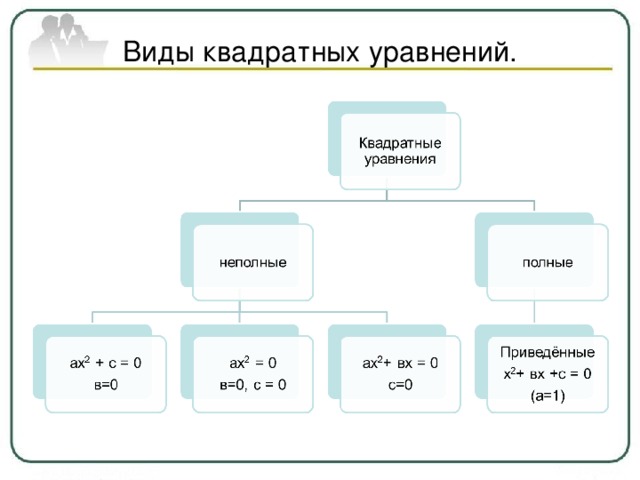
Виды квадратных уравнений.

Задание 1.

Составить из квадратного уравнения х 2 – 2х – 8 = 0 три вида неполных квадратных уравнений, ориентируясь на диагностическую таблицу.

Решить полученные уравнения.

Диагностическая таблица

Решение квадратных уравнений

неполных

полных

ах 2 + вх = 0 (с = 0)

Использование формулы корней

(через Д)

ах 2 + с = 0 ( в = 0)

Применение формулы корней чётного

второго коэффициента

ах 2 = 0 ( в = 0, с=0)

Применение теоремы Виета

Выделение квадрата двучлена

Графический способ

Набрано баллов

Оценка

Проверь себя.

1). х 2 - 2х = 0

х ∙ (х – 2)=0

х = 0 или х – 2 = 0

х = 0 х = 2

Ответ: х 1= 0 ; х 2 = 2

2). х 2 - 8 = 0

х 2 = 8

Ответ: х 1= - ; х 2 =

3). х 2 = 0

х = 0

Ответ: х = 0

0, уравнение имеет два корня х= х 1 = х 1 = -2 х 2 = х 2 = 4 Ответ: х 1 = - 2; х 2 = 4" width="640"

Задание 2.

Решить квадратное уравнение х 2 – 2х – 8 = 0

Д = в 2 - 4ас Д = (- 2) 2 – 4 ∙ ( - 8) = 36

Д 0, уравнение имеет два корня

х=

х 1 =

х 1 = -2

х 2 =

х 2 = 4

Ответ: х 1 = - 2; х 2 = 4

Теорема Виета

х 1 ∙ х 2 = - 8,

х 1 + х 2 = 2.

Ответ: х 1 = - 2, х 2 = 4

0, значит, уравнение имеет два корня х = Ответ: х 1 = - 2; х 2 = 4" width="640"

Формула чётного второго коэффициента

х 2 – 2х – 8 = 0

Д 1 =( ) 2 - ас Д 1 = (- 1) 2 – 1∙( - 8) = 9

Д 1 0, значит, уравнение имеет два корня

х =

Ответ: х 1 = - 2; х 2 = 4

Выделение квадрата двучлена

х 2 – 2х – 8 = 0

х 2 – 2х + 1 – 9 = 0

(х – 1) 2 = 9

х – 1 = - 3 или х – 1 = 3

х = - 2 х = 4

Ответ: х 1 = - 2; х 2 = 4

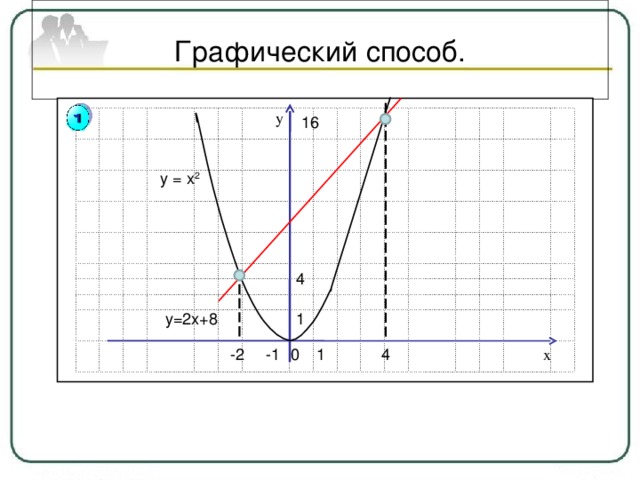
Графический способ.

Найди приз.

Определить р и х 2 в квадратном уравнении

х 2 – рх + 15 = 0, если х 1 = 3.

Найденное значение х 2 укажет номер кабинета, где лежит приз, р – номер парты (если считать от окна).

Способ группировки

х 2 – 2х – 8 = 0

(х 2 – 4) + (- 2х - 4)= 0

(х -2)(х+2) – 2(х+2) = 0

(х +2)(х – 2 – 2) = 0

(х+2)(х - 4)= 0

х + 2 = 0 или х - 4 = 0

Ответ: х 1 = - 2; х 2 = 4

Предмет: Математика

Категория: Презентации

Целевая аудитория: 8 класс

Скачать
Презентация для урока на тему «Квадратные уравнения»

Автор: Cеледец Алена Михайловна

Дата: 16.03.2016

Номер свидетельства: 306642

Похожие файлы

Урок-презентация по алгебре "Решение квадратных уравнений"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(109) "Урок-презентация по алгебре "Решение квадратных уравнений" "
    ["seo_title"] => string(69) "urok-priezientatsiia-po-alghiebrie-rieshieniie-kvadratnykh-uravnienii"
    ["file_id"] => string(6) "112354"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1408543123"
  }
}

Конспект урока по алгебре по теме "Квадратные уравнения" и презентация

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(129) "Конспект урока по алгебре по теме "Квадратные уравнения" и презентация"
    ["seo_title"] => string(72) "konspiekturokapoalghiebriepotiemiekvadratnyieuravnieniiaipriezientatsiia"
    ["file_id"] => string(6) "325297"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1462899593"
  }
}

Обобщающий урок по теме "Квадратные уравнения"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(86) "Обобщающий урок по теме "Квадратные уравнения" "
    ["seo_title"] => string(56) "obobshchaiushchii-urok-po-tiemie-kvadratnyie-uravnieniia"
    ["file_id"] => string(6) "145964"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1419020789"
  }
}

Презентация к уроку по теме "Квадратные уравнения"

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(92) "Презентация к уроку по теме "Квадратные уравнения""
    ["seo_title"] => string(57) "priezientatsiia-k-uroku-po-tiemie-kvadratnyie-uravnieniia"
    ["file_id"] => string(6) "264360"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1449686760"
  }
}

Конспект урока математики, презентация для урока 8 классе по теме:"Квадратные уравнения .Теорема Виета."

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(190) "Конспект урока математики, презентация для урока 8 классе по теме:"Квадратные уравнения .Теорема Виета." "
    ["seo_title"] => string(115) "konspiekt-uroka-matiematiki-priezientatsiia-dlia-uroka-8-klassie-po-tiemie-kvadratnyie-uravnieniia-tieoriema-viieta"
    ["file_id"] => string(6) "111720"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1407835916"
  }
}

Презентация для урока на тему «Квадратные уравнения»

Просмотр содержимого документа «Презентация для урока на тему «Квадратные уравнения»»

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Презентация для урока на тему «Квадратные уравнения»»