Через тернии к звездам
Алгебра 8 класс
учитель математики МБОУ-СОШ № 11 г.
Искитима Новосибирской области
высшей квалификационной категории
Овсянникова Татьяна Степановна
2014 год
Урок был проведён в рамках Дня открытых дверей (городское мероприятие). Общим девизом для всех уроков является девиз: «Я живу в России».
«Через тернии к звездам»
Тема: Квадратные уравнения. Теорема Виета.
Тип урока: Урок обобщения и систематизации знаний.
Цель урока: Создать максимальные условия для проведения ценностно-эмоционального отношения учащихся к знаниям.
Задачи урока:
Образовательные: Систематизация и обобщение знаний по теме.
Воспитательные: Развитие чувства патриотизма средствами урока математики. Формирование ответственности перед коллективом, организованности, дисциплинированности, чувства долга, инициативы и творчества в учебном процессе.
Развивающие: Развитие познавательного интереса к предмету.
«Вступительное слово учителя»
Прежде чем объявить тему нашего урока, хочу напомнить что с 7-23 февраля 2014 г. В России походили Зимние Олимпийские игры.
Олимпийские игры являются крупными спортивными событиями, в которых тысячи спортсменов со всего мира соревнуются в различных видах спорта. К этим играм готовятся в течении 4-х лет . В итоге мы видим красивые танцы на льду, виртуозные выступления сноубордистов, захватывающие гонки биатлонистов и т.д.
Но за этим стоит ежедневная, многогодовая подготовка, тяжёлая и упорная работа.
Результаты Олимпиады- это достижения страны.
Ваши знания ребята- это достижения школы, а это будущие достижения России.
Для учителя высшая награда- это достижения его учеников. Школа всегда гордиться своими выпускниками. Про своих учеников ,добившихся успехов- мы говорим:»Зажглась ещё одна звёздочка» . Но как не лёгок бывает путь к победе. И учиться преодолевать трудности ребята начинают в школе при изучении различных разделов школьного курса.
Не исключение и математика. Так одним из разделов алгебры 8-го класса является изучение квадратных уравнений. Это очень важная тема.
Завершая учебный год проверим свои знания по данной теме.
Тема нашего урока:
Через тернии к звездам
«Мышление начинается с удивления», - заметил 2500 лет назад Аристотель. Наш соотечественник Сухомлинский считал, что «чувство удивления - могучий источник желания знать, от удивления к знаниям – один шаг». А математика – замечательный предмет для удивления.
Мы совершим сегодня путешествие, которое в дальнейшем может оказаться одной из тропинок познания нового неизвестного. Создадим три экипажа. У каждого свой маршрут. А цель одна – показать свои знания на всех этапах. ( У каждого на парте свой маршрутный лист).
Начнем с разминки. (смотреть слайд в презентации)
1.Какое уравнение называется квадратным?
2. Если а=1, то как называется квадратное уравнение?
3. Найти из представленных примеров приведенные уравнения.
а) 5х²+4=0
б) -11х²+6х=0
в) х²+4х+10=0
г) 1,8х²=0
4. Определить знак корней квадратных уравнений.
а) х²+15х+2=0
б) х²+4х-10=0
в) х²-15х+2=0
г) х²-4х-10=0
5. решить уравнения.
а) -0,1х²=0
б) х²-13=0
в) х²+49=0
г) х²+6х+5=0
д) х²-6х+5=0
е) х²-5х+6=0
А теперь в путь!
Путешествие будет нелегким. Чтобы продвинуться вперед, нужно показать свои знания. Каждый экипаж пойдет по своей лесенке.
Решаем задание №1 маршрутного листа.
Слово учителя: Что означает число «1! Для нашей Олимпиады?
ОТВЕТ:МЫ ПЕРВЫЕ на Олимпиаде!
( на доске прикрепляется цифра «1»)
При правильном выборе решения, получается слово. Затем слова записывают на доске в пропущенные места.
[Счет и вычисления – основа порядка в голове]
Подводятся итоги, кто быстрее - помогает отстающим.
Мы справились с одним этапом нашего восхождения и двигаемся вперед.
(Задания усложняются)
Решаем задание №2 маршрутного листа.
Слово учителя: Что означает число «2» для Олимпиады?
Ответ: Это были вторые Олимпийские игры в нашей стране.
( на доске прикрепляется цифра «2»)
1 группа:
а) 5х²-8х+3=0;
б) 3х²-х+18=0.
2 группа:
а) 5х²-6х+1=0;
б) х²-14х-15=0.
3 группа:
а) 2х²+3х+1=0;
б) 2х²-3х-35=0.
Проверяем правильность решения. (Ответы см. презентацию),
Мы говорим с ребятами о найденных корнях уравнений.
«1»-мы абсолютные победители Олимпиады!
«Корней нет»-нам было трудно и не каждый день были победы.
«15»-самая юная участница Олимпиады Юлия Липницкая- ей 15 лет.
«5»-пять медалей в фигурном катании.
(на доске прикрепляются числа «15» и «5»)
Заслуженный отдых – привал.
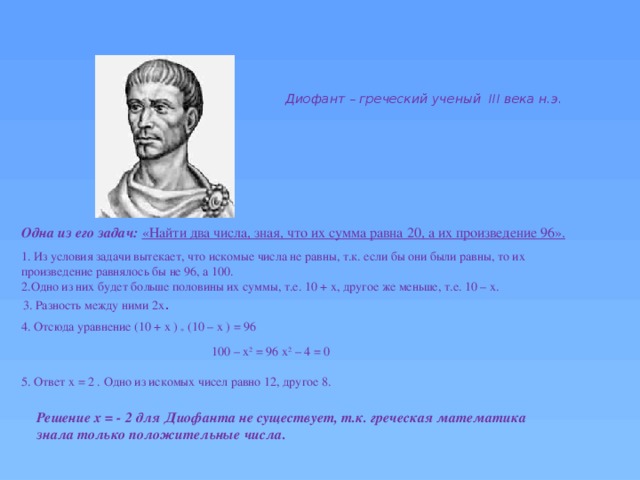
Послушаем историю возникновения квадратных уравнений. Представитель каждого экипажа рассказывает немного из истории квадратных уравнений. (см. презентацию)
Чем еще можно заняться на коротком отдыхе? Конечно же, разгадать кроссворд.
У всех на партах кроссворд.
| 
| По вертикали: Число корней квадратного уравнения при D0 Число корней квадратного уравнения при D=0 Квадратное уравнение, в котором первый коэффициент равен единице Где впервые решили квадратное уравнение Квадратное уравнение, в котором b=0 или c=0 Число корней квадратного уравнения, при D 7)Учёный, доказавший теорему о свойстве корней квадратного уравнения По горизонтали: Различитель квадратного уравнения.
|
(Ответы к кроссворду смотри презентации.)
После небольшой передышки снова в путь. Дорога становится сложнее. Мы первопроходцы, наша задача проложить себе дорогу, т.е. уметь составлять квадратные уравнения.
Маршрутный лист. Задание №3
Слово учителя: Что означает число «3» для Олимпиады?
Ответ: »3»-Медали в фигурном катании.
В последний день Олимпиады наши лыжники заняли три призовых места.
«33»-медали в нашем зачёте.
(прикрепляется на доске числа «3»и «33»)
Вопрос: Сколько каких медалей было?
Ответ: «13»-золотых. «11»-серебряных и «9»-бронзовых
(Прикрепляем на доске числа «13», «11» «9»)
Слово учителя: Составим квадратные уравнения, корнями которых являются числа:
| 1 группа: а) 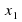 =13; =13; 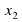 = 9; = 9; б) 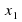 = -11; = -11; 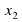 =9; =9; | 2 группа: а) 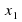 =-13; =-13; 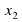 = -9; = -9; б) 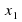 = 11; = 11; 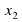 = 9; = 9; | 3 группа: а) 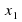 =11; =11; 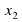 = -9; = -9; б) 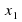 = -13; = -13; 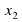 =-11; =-11; |
(Ответы смотри презентацию.)
Совсем немного до цели. Участок пути остался самый трудный.
Маршрутный лист. Задание №4
Слово учителя: В нашем классе ребята занимаются спортом- это будущие чемпионы. Говорим о спортивных достижениях класса.
Выполняем задание№4
| 1 группа: х²+Кх-14=0 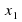 = -2 = -2
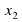 -? К- ? -? К- ?
| 2 группа: х²+6х+К=0 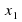 = -7 = -7
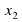 -? К- ? -? К- ?
| 3 группа: х²+Кх-10=0 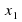 = 5 = 5
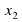 -? К- ? -? К- ?
|
(Ответы смотри презентацию.)
На протяжении всего пути вы помогали друг другу. Последние шаги каждый должен пройти самостоятельно. Поэтому еще одна минута отдыха. А что для отдыха может быть лучше, чем хорошая песня!
(Поем классом песню под гитару.)
Песня на мотив «Синяя птица» группы «Машина времени»
Мы в такие ходили дали,
Что не очень-то и дойдешь.
Уравнения мы решали,
Не взирая на снег и дождь.
Но откуда они появились
Пусть история даст ответ.
Мы – охотники за удачей
И преград нам в науке нет.
Уравнения мы решаем.
Сразу многое не поймешь.
Но учитель нам помогает
И до цели своей дойдешь.
Математика – вот наука.
Развивает она умы.
Не страшна никакая скука,
Коль задачи все решены!
Слово учителя: Ещё раз напомним с вами ребята, что означают числа, прикреплённые на доске.
Проверочный заключительный тест.
Слово учителя:
Завершая урок, мне хочется надеяться, что и наш класс оставит яркий след в истории родной школы. И изучая квадратные уравнения через n-е количество лет, учитель мог бы про вас сказать, что в Олимпийский год – 2014, восьмые классы были настоящими звездочками.
ПРИЛОЖЕНИЕ:
Маршрутный лист – 3 варианта.
Кроссворд.
Песня (на мотив «Синяя птица»)
Тест – 2 варианта.
Презентация. (отдельный файл)
Фото с урока.
|
I группа
№1 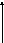 х2-8х+7=0 х2-8х+7=0
7; 1 – а -7; -1 – с -7; 1 – о х2+4х-5=0 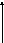 -5; 1 – в -5; 1 – в
5; -1 – о -5; -1 – н х2-5=0 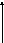 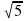 – с – с
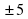 – н – н 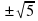 - о - о 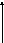 х2+25=0 х2+25=0
5 – с 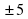 – о – о Нет к. - н 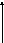 17х2=0 17х2=0
0 – с 17 - о нет к. - н 2х2=8 2 – н 0 - в 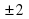 – о – о
|
№2 а) 5х²-8х+3=0; б) 3х²-х+18=0.
№3 а) 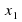 =13; =13; 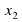 = 9; = 9; б) 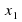 = -11; = -11; 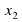 =9; =9;
№4 х²+Кх-14=0 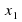 = -2 = -2
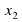 -? К- ? -? К- ?
|
| II группа
№1
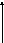 х2+8х+7=0 х2+8х+7=0
7; 1 – р -7; -1 – а -7; 1 – к 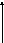 х2-4х-5=0 х2-4х-5=0
5; -1 – к -5; 1 – о -5; -1 – д 7х2-7=0 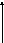 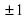 – д – д
1 - о 0 - к х2-7=0 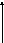 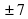 – к – к
0 – н 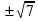 - я - я  х2+9=0 х2+9=0
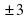 – к – к 3– о Нет к. - р  19х2=0 19х2=0
0 – о 19 - д нет к. - к 4х2=16 0 – р 2 - о 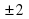 – п – п
|
№2 а) 5х²-6х+1=0; б) х²-14х-15=0.
№3 а) 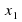 =-13; =-13; 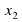 = -9; = -9; б) 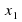 = 11; = 11; 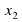 = 9; = 9;
№4 х²+6х+К=0 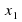 = -7 = -7
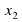 -? К- ? -? К- ?
|
|
III группа
№1 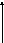 х2+4х-5=0 х2+4х-5=0
-5; 1 – е -1; -5 – л -1; 5 – о х2-5х+6=0  2; 3 – в 2; 3 – в
-2; -3 – о 2; -3 – л х2-11=0  Нет к. - в Нет к. - в
 - л - л  - о - о  х2+16=0 х2+16=0
4 – г  – о – о Нет к. - л  15х2=0 15х2=0
0 – о 15 - л  – г – г 5х2=20 0 – л 2 - о 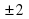 – г – г
|
№2 а) 2х²+3х+1=0; б) 2х²-3х-35=0.
№3 а) 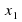 =-9; =-9; 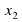 = 11; = 11; б) 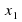 = -13; = -13; 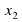 =-11; =-11;
№4 х²+Кх-10=0 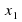 = 5 = 5
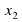 -? К- ? -? К- ?
|
Кроссворд
|
| По вертикали: Число корней квадратного уравнения при D0 Число корней квадратного уравнения при D=0 Квадратное уравнение, в котором первый коэффициент равен единице Где впервые решили квадратное уравнение Квадратное уравнение, в котором b=0 или c=0 Число корней квадратного уравнения, при D Учёный, доказавший теорему о свойстве корня квадратного уравнения По горизонтали: Различитель квадратного уравнения.
|
Песня на мотив «Синяя птица» группы «Машина времени»
Мы в такие ходили дали,
Что не очень-то и дойдешь.
Уравнения мы решали,
Не взирая на снег и дождь.
Но откуда они появились
Пусть история даст ответ.
Мы – охотники за удачей
И преград нам в науке нет.
Уравнения мы решаем.
Сразу многое не поймешь.
Но учитель нам помогает
И до цели своей дойдешь.
Математика – вот наука.
Развивает она умы.
Не страшна никакая скука,
Коль задачи все решены!
Проверочный заключительный тест.
Через тернии к звёздам.
8 «Б»
5

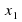 =13;
=13; 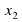 = 9;
= 9; 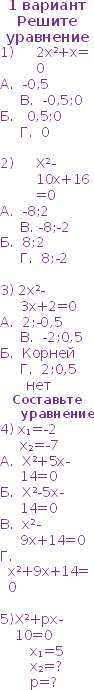
 х2-8х+7=0
х2-8х+7=0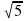 – с
– с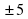 – н
– н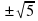 - о
- о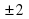 – о
– о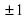 – д
– д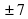 – к
– к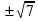 - я
- я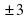 – к
– к














 0 Число корней квадратного уравнения при D=0 Квадратное уравнение, в котором первый коэффициент равен единице Где впервые решили квадратное уравнение Квадратное уравнение, в котором b=0 или c=0 Число корней квадратного уравнения, при DУчёный, доказавший теорему о свойстве корней квадратного уравнения По горизонтали: 8. Различитель квадратного уравнения. 7 2 3 4 6 1 8" width="640"
0 Число корней квадратного уравнения при D=0 Квадратное уравнение, в котором первый коэффициент равен единице Где впервые решили квадратное уравнение Квадратное уравнение, в котором b=0 или c=0 Число корней квадратного уравнения, при DУчёный, доказавший теорему о свойстве корней квадратного уравнения По горизонтали: 8. Различитель квадратного уравнения. 7 2 3 4 6 1 8" width="640"






















