Урока алгебры 9 класс по теме "Решение квадратных уравнений". Рассмотрены способы решения квадратных уравнений: графически, по формуле, способ выделения полного квадрата, разложение на множители и т.д. Материал интересен для повторения темы "Квадратные уравнения" в период подготовки к ГИА.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок-презентация по алгебре "Решение квадратных уравнений"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок-презентация по алгебре "Решение квадратных уравнений" »
Полезное для учителя
Распродажа видеоуроков!
1540 руб.
2560 руб.
1060 руб.
1760 руб.
1540 руб.
2560 руб.
1630 руб.
2710 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства









 0,- 2 КОРНЯ. D=0 ,-1 КОРЕНЬ. D
0,- 2 КОРНЯ. D=0 ,-1 КОРЕНЬ. D



 0,то уравнение имеет два одинаковых по знаку корня и это зависит ОТ КОЭФФИЦИЕНТА P . Е СЛИ Р 0 , ТО ОБА КОРНЯ ОТРИЦАТЕЛЬНЫ. Х² +8 Х +7 =0,Т.К. Р=8 , q =7 , ТО Х 1 =-7,Х 2 =-1. Е СЛИ Р Х² -3 Х +2 =0, Т.К. Р=-3, q =2 , ТО Х 1 =1;Х 2 =2" width="640"
0,то уравнение имеет два одинаковых по знаку корня и это зависит ОТ КОЭФФИЦИЕНТА P . Е СЛИ Р 0 , ТО ОБА КОРНЯ ОТРИЦАТЕЛЬНЫ. Х² +8 Х +7 =0,Т.К. Р=8 , q =7 , ТО Х 1 =-7,Х 2 =-1. Е СЛИ Р Х² -3 Х +2 =0, Т.К. Р=-3, q =2 , ТО Х 1 =1;Х 2 =2" width="640"






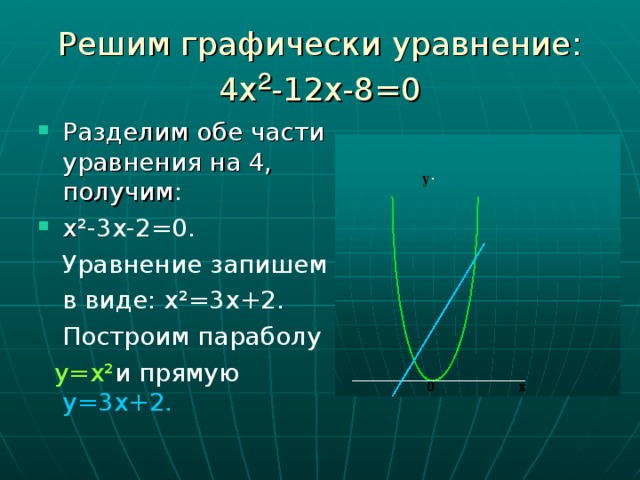
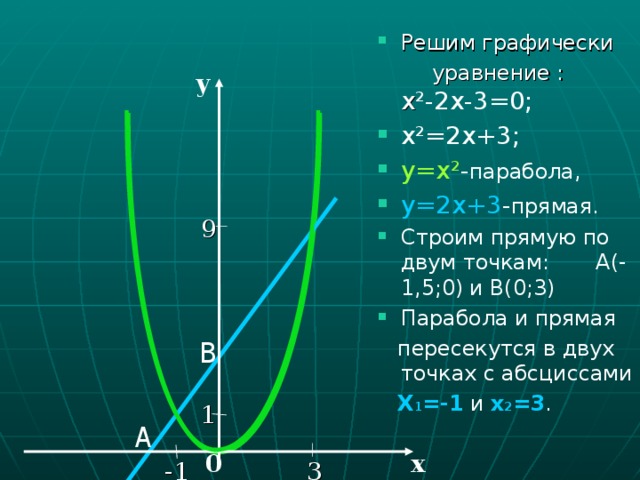
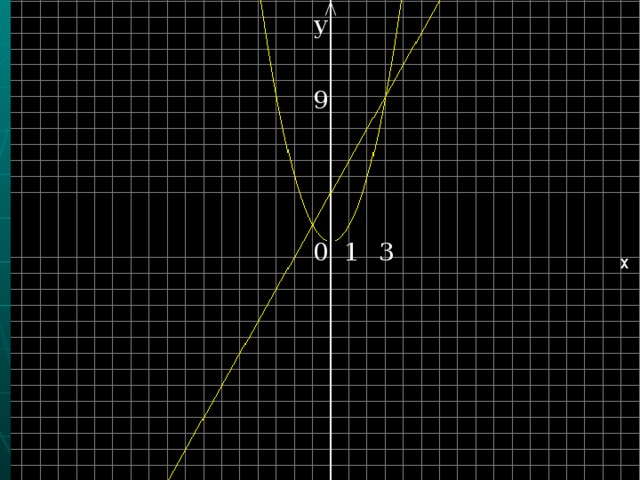

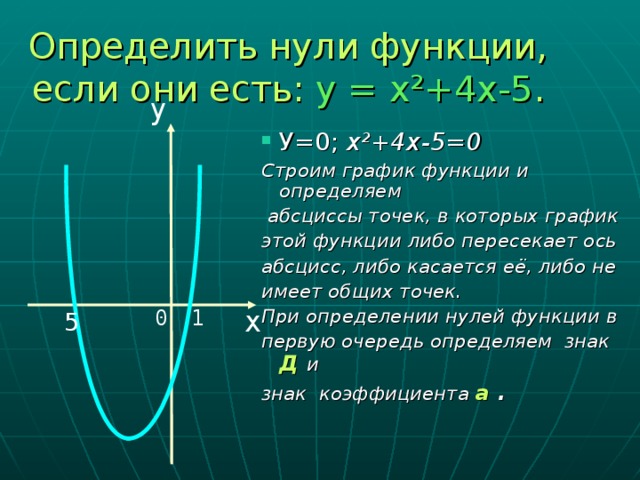
 0, а 3) Д 0; 1) Д 0, а 0; 4) Д 5) Д = 0, а 0 . 1 y y 2 x x y y 1 2 5 3 6 4 3 4 1 2 5 3 6 4 x 1 2 5 3 6 4 x y 5 y 6 1 2 5 3 6 4 x 1 2 5 3 6 4 x" width="640"
0, а 3) Д 0; 1) Д 0, а 0; 4) Д 5) Д = 0, а 0 . 1 y y 2 x x y y 1 2 5 3 6 4 3 4 1 2 5 3 6 4 x 1 2 5 3 6 4 x y 5 y 6 1 2 5 3 6 4 x 1 2 5 3 6 4 x" width="640"





















