Медианы, биссектрисы и высоты треугольника

КРАТКОЕ ОПИСАНИЕ РАБОТЫ.

Презентация «Медиана, биссектриса, высота треугольника» составлена к уроку изучения нового материала по данной теме.

Основные цели урока

- формирование умения построения и распознавания медиан, биссектрис и

высот треугольника;

- развитие умения анализировать и сравнивать;

- развитие внимания, аккуратности и самостоятельности.

Презентация используется на этапах изучения нового материала и первичного закрепления новых знаний.

Слайды № 2 и № 3 используются при введении понятия перпендикуляра, слайды № 4 и № 5 при изучении понятия высоты, слайд № 6 при введении понятия медианы и слайд № 7 при введении понятия биссектрисы треугольника.

Слайды № 8 - № 11 используются на этапе рефлексии.

КРАТКИЕ РЕКОМЕНДАЦИИ К ИСПОЛЬЗОВАНИЮ

Изучение нового материала проводится в ходе выполнения практических заданий.

1) Начертите прямую b и точку В, которая не лежит на прямой b. Через точку В проведите прямую а, перпендикулярную прямой b. Точку пересечения прямых обозначьте Н. Отрезок ВН – перпендикуляр, проведенный из точки В к прямой b. (слайд № 2)

2) Сформулируйте определение перпендикуляра (проверка по тексту учебника). Запишите определение в тетрадь.

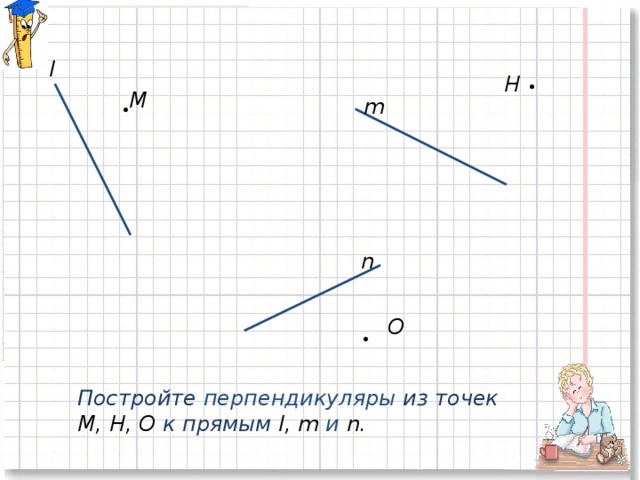
3) Скопируйте рисунок (слайд№ 3). Постройте перпендикуляры из данных точек к данным прямым. Обозначьте основание каждого перпендикуляра буквой. Запишите с помощью символа «», что изображено на рисунке.

4) Постройте ? АВС и проведите перпендикуляр из вершины А к прямой, содержащей противолежащую сторону. Основание перпендикуляра обозначьте буквой Н.

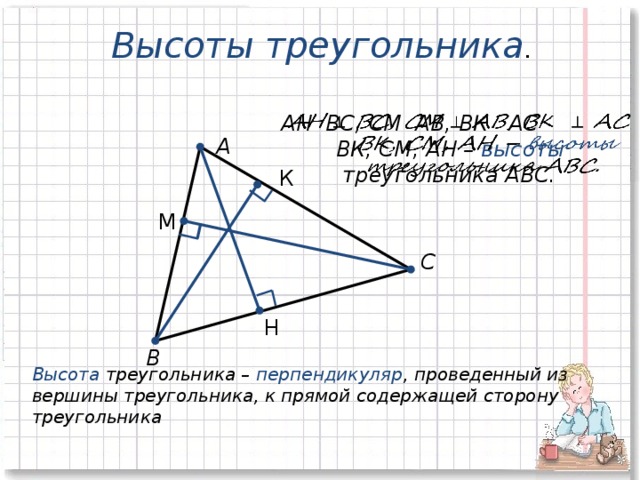
5) Вы провели высоту треугольника АВС. Сформулируйте определение высоты треугольника и запишите его в тетрадь (работа с учебником) (слайд № 4).

Проведите высоты СМ и ВК.

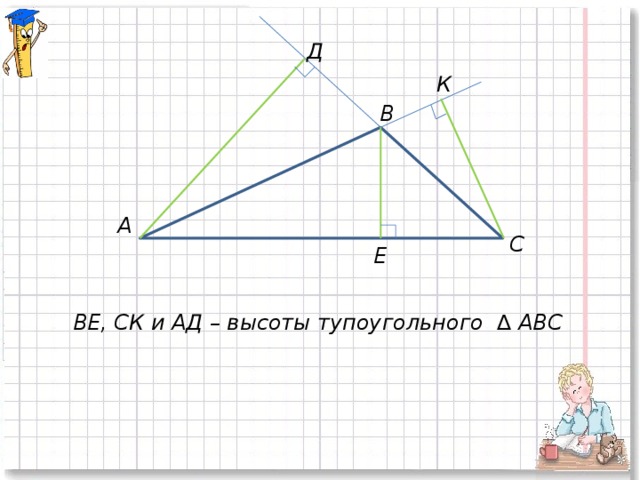
6) Постройте тупоугольный треугольник АВС и проведите все высоты.

(обсуждение проблемной ситуации, работа в группах) (слайд № 5).

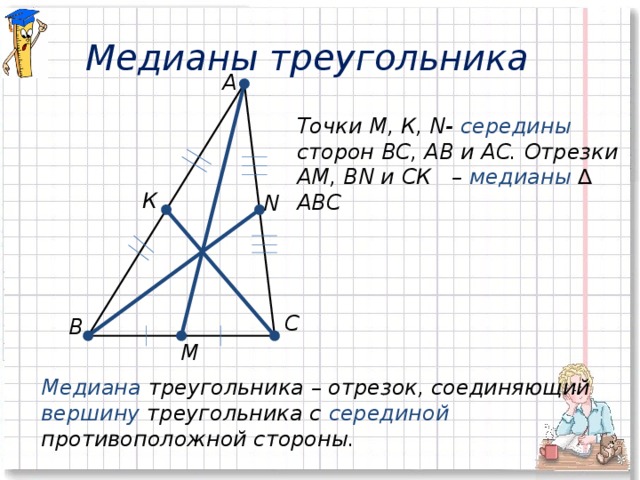
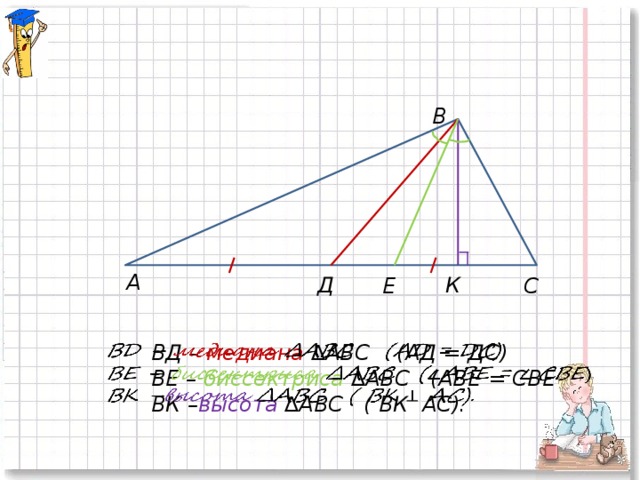
7) Середины сторон АВ, ВС и АС треугольника АВС обозначьте буквами К, М и N соответственно. Проведите отрезок, соединяющий вершину А с серединой противолежащей стороны. Отрезок АК – медиана треугольника АВС.

8) Сформулируйте определение медианы и запишите в тетрадь. Проведите медианы из вершин В и С, запишите их названия. Выпишите пары равных отрезков на рисунке (слайд № 6).

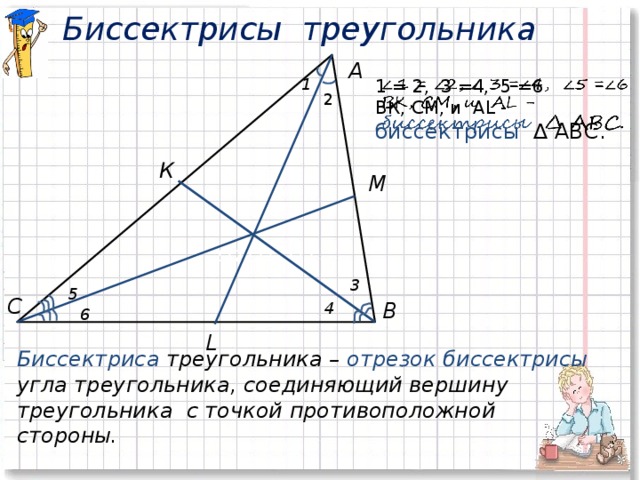
9) В треугольнике АВС проведите биссектрису угла А. Точку пересечения биссектрисы и стороны ВС обозначьте буквой L. AL – биссектриса треугольника АВС. Сформулируйте определение биссектрисы треугольника. Проведите биссектрисы углов В и С (слайд № 7).

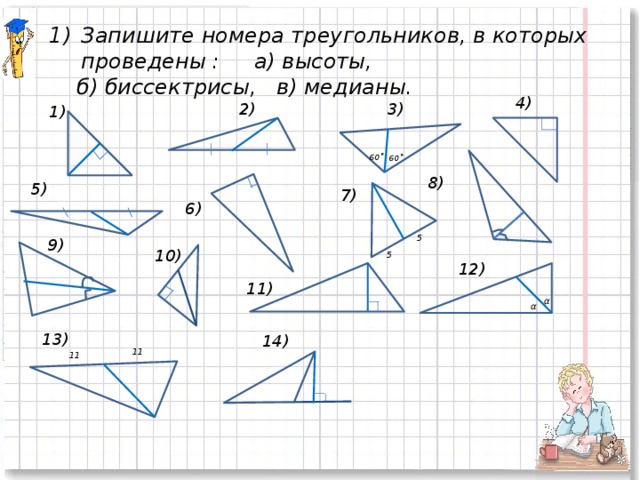
10) Анализ, сравнение и систематизация полученных знаний (слайд № 8).

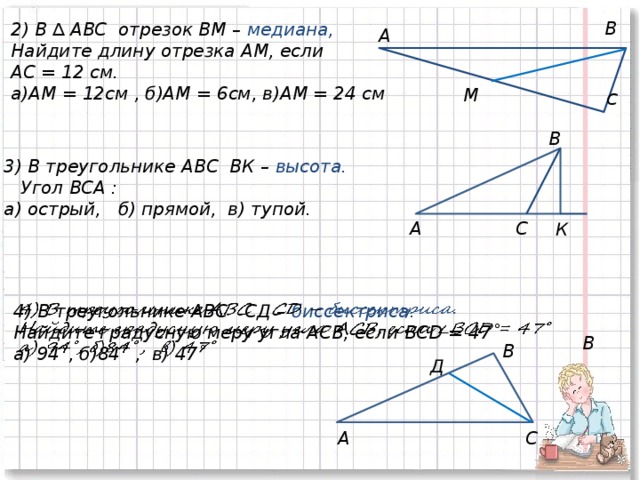
11) Тест с последующими самопроверкой и взаимопроверкой

(слайды №9, 10, 11).

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Медианы, биссектрисы и высоты треугольника »

Тема:

Медианы,

биссектрисы

и высоты

треугольника.

Автор Мальцева Марина Ивановна,

учитель математики

МБОУ СОШ № 55 г. Иркутска

Отрезок BН – перпендикуляр , проведенный из

точки B к прямой b, если:

1) BН b;

2) B b, Н b.

Точка Н – основание перпендикуляра.

•

Постройте перпендикуляры из точек

М, Н, О к прямым l, m и n.

Высоты треугольника .

АН ВС, СМ АВ, ВК АС

ВК, СМ, АН – высоты

треугольника АВС.

Высота треугольника – перпендикуляр , проведенный из

вершины треугольника, к прямой содержащей сторону

треугольника

ВЕ, СК и АД – высоты тупоугольного ∆ АВС

Медианы треугольника

Точки М, К, N- середины сторон ВС, АВ и АС. Отрезки АМ, ВN и СК – медианы ∆ АВС

Медиана треугольника – отрезок, соединяющий

вершину треугольника с серединой

противоположной стороны.

Биссектрисы треугольника

2222222222

1 = 2, 3 =4, 5 =6

ВК, СМ, и AL - биссектрисы ∆ АВС.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

ВД – медиана ∆АВС (АД = ДС)

ВЕ – биссектриса ∆АВС (АВЕ = СВЕ

ВК – высота ∆АВС ( ВК АС).

Запишите номера треугольников, в которых проведены : а) высоты,

Запишите номера треугольников, в которых проведены : а) высоты,

б) биссектрисы, в) медианы.

60˚

10)

12)

11)

13)

14)

2) В ∆ АВС отрезок ВМ – медиана, Найдите длину отрезка АМ, если

АС = 12 см.

а)АМ = 12см , б)АМ = 6см, в)АМ = 24 см

3) В треугольнике АВС ВК – высота.

Угол ВСА :

а) острый, б) прямой, в) тупой.

4) В треугольнике АВС СД – биссектриса.

Найдите градусную меру угла АСВ, если BCD = 47˚

а) 94˚, б)84˚ , в) 47˚

Ответы к тесту:

а) 1, 4, 6,10, 11, 14

б) 3, 8, 9, 12

в) 2, 5, 7, 13

2) б

3) в

4) а

Предмет: Математика

Категория: Презентации

Целевая аудитория: 7 класс

Скачать
Медианы, биссектрисы и высоты треугольника

Автор: Мальцева Марина Ивановна

Дата: 03.10.2015

Номер свидетельства: 235840

Похожие файлы

Конспект урока на тему "Медианы, биссектрисы, высоты треугольника"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(122) "Конспект урока на тему "Медианы, биссектрисы, высоты треугольника" "
    ["seo_title"] => string(68) "konspiekt-uroka-na-tiemu-miediany-bissiektrisy-vysoty-trieughol-nika"
    ["file_id"] => string(6) "103024"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1402564055"
  }
}

"Медиана, биссектриса,высота треугольника"

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(79) ""Медиана, биссектриса,высота треугольника" "
    ["seo_title"] => string(43) "miediana-bissiektrisa-vysota-trieughol-nika"
    ["file_id"] => string(6) "124799"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1414785214"
  }
}

"Медиана, биссектриса и высота треугольника"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(82) ""Медиана, биссектриса и высота треугольника" "
    ["seo_title"] => string(45) "miediana-bissiektrisa-i-vysota-trieughol-nika"
    ["file_id"] => string(6) "127424"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1415300211"
  }
}

Урок-зачет по геометрии на тему: "Треугольники".

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(87) "Урок-зачет по геометрии на тему: "Треугольники". "
    ["seo_title"] => string(52) "urok-zachiet-po-ghieomietrii-na-tiemu-trieughol-niki"
    ["file_id"] => string(6) "194079"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1427725536"
  }
}

Конспект урока геометрии на тему "Треугольник"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(85) "Конспект урока геометрии на тему "Треугольник""
    ["seo_title"] => string(45) "konspiekturokaghieomietriinatiemutrieugholnik"
    ["file_id"] => string(6) "299385"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1456505518"
  }
}

Медианы, биссектрисы и высоты треугольника

Просмотр содержимого документа «Медианы, биссектрисы и высоты треугольника »

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Медианы, биссектрисы и высоты треугольника »