Логарифмическая функция и ее свойства

"Логарифмическая функция и ее свойства"

ГАОУ СПО «ККСД»

Преподаватель Филимонова Ольга Николаевна

г. Калуга

Есть в математике тема одна,

Логарифмической функцией называется она,

Логарифм появился, чтобы легче считать,

Логарифм – ПОКАЗАТЕЛЬ,

Это надо знать!

Цель урока:

Обобщить и систематизировать знания о свойствах логарифмической функции

Использование свойств логарифмической функции для выполнения заданий с логарифмами

Выполнять преобразования выражений

Находить значения выражений

Сравнивать выражения

Выполнять логарифмирование и потенцирование выражений

Строить графики логарифмических функций

Решать алгебраические неравенства

Решать логарифмические неравенства

Решать логарифмические уравнения

«Я старался, насколько мог и умел, отделаться от трудности и скуки вычислений, докучность которых обычно отпугивает весьма многих от изучения математики»

Джон Непер

(Шотландия, 17 век)

Из истории логарифмов

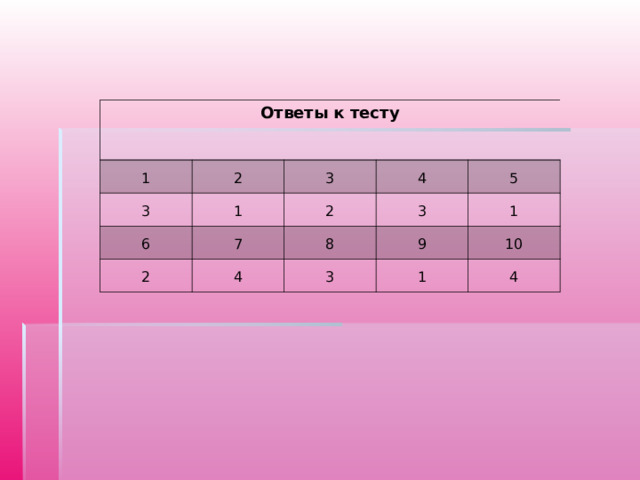
Слово логарифм происходит от греческого λογοφ ( число ) и ρίνμοφ ( отношение ) и переводится, следовательно, как отношение чисел . Выбор изобретателем (1594 г.) логарифмов Джоном Непером такого названия объясняется тем, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом арифметической прогрессии, а другое – геометрической.

Русский математик Аничков Д. С. о логарифмах

«Ежели под геометрическою прогрессиею, начинающеюся с единицы, подписана будет арифметическая прогрессия, начинающаяся с нуля, то числа, внизу подписанные, называются для верхних – логарифмы.

Положим, что даны прогрессии:

геом. 1, 2, 4, 8, 16, 32, 64, 128, 256,

арифм. 0, 1, 2, 3, 4, 5, 6, 7, 8.

Тогда логарифм 1 будет 0;

логарифм 4 будет 2;

а логарифм 32 будет 5 и проч.»

0) 2. а 0 = 1 (а ≠ 0) 3. а 1 = а Свойства: 1. а х . а у = а х + у 2. а х : а у = а x - y 3. ( а х ) у = а х у при а 0, a ≠ 1, x 0, y 0 Определения: 1. log a x = n а п = х, т.е. a log a x = x 2. log a 1 = 0 3. log a a = 1 Свойства : 1. log a ( x . y ) = log a x + log a y 2. log a x / y = log a x – log a y 3. log a x n = n . log a x" width="640"

С Т Е П Е Н Ь

Л О Г А Р И Ф М

Определения:

1. а п = х (а 0)

2. а 0 = 1 (а ≠ 0)

3. а 1 = а

Свойства:

1. а х . а у = а х + у

2. а х : а у = а x - y

3. ( а х ) у = а х у

при а 0, a ≠ 1, x 0, y 0

Определения:

1. log a x = n а п = х, т.е.

a log a x = x

2. log a 1 = 0

3. log a a = 1

Свойства :

1. log a ( x . y ) = log a x + log a y

2. log a x / y = log a x – log a y

3. log a x n = n . log a x

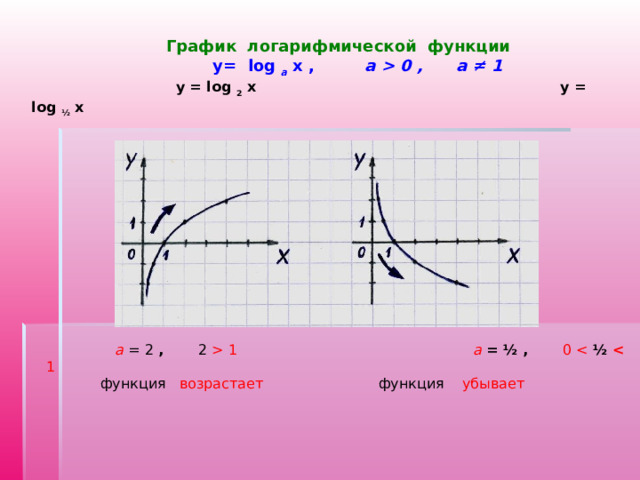0 , a ≠ 1 y = log 2 x y = log ½ x а = 2 , 2 1 a = ½ , 0 ½ 1 функция возрастает функция убывает" width="640"

График логарифмической функции

у= log a x , a 0 , a ≠ 1

y = log 2 x y = log ½ x

а = 2 , 2 1 a = ½ , 0 ½ 1

функция возрастает функция убывает

1/8 После приведения к основанию ½: ( ½ ) 2 ( ½ ) 3 После логарифмирования по основанию 10: lg ( ½ ) 2 lg ( ½ ) 3 По свойству логарифмов: 2 lg ( ½ ) 3 lg ( ½ ) После сокращения на lg ( ½ ): 2 3 В чём ошибка? 2 3 ?!" width="640"

Очевидно, что ¼ 1/8

После приведения

к основанию ½: ( ½ ) 2 ( ½ ) 3

После логарифмирования

по основанию 10: lg ( ½ ) 2 lg ( ½ ) 3

По свойству логарифмов: 2 lg ( ½ ) 3 lg ( ½ )

После сокращения на lg ( ½ ): 2 3

В чём ошибка?

2 3 ?!

ЗАПОМНИ !

Логарифм и ОДЗ

вместе

трудятся

везде!

Сладкая парочка!

Два сапога – пара!

ОН

- ЛОГАРИФМ !

ОНА

-

ОДЗ!

Два в одном!

Два берега у одной реки!

Нам не жить

друг без

друга!

Близки и неразлучны!

Ответы к тесту

1

3

2

6

1

3

2

2

4

7

5

3

8

4

3

1

9

10

1

4

Логарифмы в деятельности человека

в астрономии

в электротехнике

в животноводстве

в экономике

в музыке

в технике

и в природе

семечки подсолнуха

паутина

галактика

раковина

рога козла

По горизонтали:

• Название члена при делении
• Прямая, имеющая единственную общую точку с окружностью
• Равенство двух отношений
• Знак, меняющий значение выражения на противоположное
• Член многочлена, имеющий только числовое значение

По вертикали:

• Расстояние от начала отсчета до точки, изображающей число
• Ось координатной плоскости
• Множество точек (Х; f (Х) ) на плоскости
• Действие, определяющее сумму
• Тригонометрическая функция

Значимость логарифмов

«С точки зрения вычислительной практики, изобретение логарифмов по важности можно смело поставить рядом с другим, более древним великим изобретением индусов – нашей десятичной системой нумерации.»

Успенский Я. В.,

русский математик