«Знания должны не только ум наполнять.
Их надо применять.» А. Эйнштейн
Тема урока: Повторение «Логарифмическая функция в уравнениях».
Цель урока: повторить свойства логарифма и логарифмической функции; продолжить работу по формированию у обучающихся умений решать логарифмические уравнения и неравенства; расширить представление учащихся о логарифмической функции, применение её свойства в нестандартных ситуациях.
Оборудование: ноутбуки, запись на доске, логарифмическая линейка, Учебное пособие «Математика. Подготовка к ЕГЭ-2012»
Ход урока:
- Организационный момент.
Слайд 1: Мы сегодня применяем на работе эпиграф Эйнштейна
«Знания должны не только ум наполнять.
Их надо применять».
- Объявление темы, цели и этапов урока:
Тема и цель урока: «Логарифмическая функция в уравнениях»- повторение.
Сегодня на уроке мы вспомним свойства логарифмов, решение уравнений и неравенств и работаем по следующим этапам: слайд 3
- 1-й Логарифмическая функция и её приложение (историческая справка)
- 2 –й «Потяни за ниточку» (теоретический)
- 3-й «Логарифмическая комедия» (найдите ошибку, кто быстрее)
- 4-й «Логарифмические диковинки» ( Любое число – тремя «2»)
- 5-й «Видит око, да ум ещё дальше» (задание на прямое применение свойств логарифмической функции)
- 6-й «На приз Непера» ( самостоятельная работа)
- 7-й Подведение итогов урока, выставление оценок, задание на дом.
- слайд 4 Приступаем к 1 этапу «Логарифмическая функция и её приложение» Вам нужно было подготовить историческую справку о логарифмах. (Выступление учеников. Слайды 5 – 8)
Слайд 9 Переходим ко 2-йму этапу: «Потяни за ниточку» (теоретический) Внимательно меня слушаем, отвечаем по очереди:
- Дайте определение логарифма числа по заданному основанию.
( Логарифмом числа в по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число в.)
- Запишите основное Логарифмическое тождество ( )
- Основные свойства логарифмов (а≠0, а ?0, х ?0)
- Формула логарифмического перехода от одного основания к другому основанию
- Какие Логарифмы называются десятичными? (по основанию 10)
- Какие Логарифмы называются Натуральными? (по основанию е)
- Какова область определения и область значения функции У=LOGа Х?
- В каком случае функция У= LOGа Х является возрастающей, в каком убывающей?
- Найдите значение выражения, имеющие смысл:
- 5, LOG2 0, LOG5 (-4), LOG4 1, LOG5 5, LOG3( )
- Найти верные равенства:
- 8 = 3, LOG2 4 = -2, LOG2 4 = 2, LOG2 (-16)= 2
- Какой знак имеет функция у= LOG2 х на промежутке (0;1)
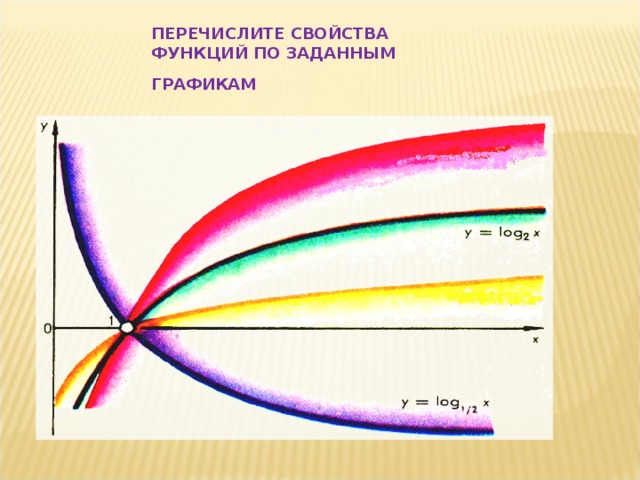
- ПЕРЕЧИСЛИТЕ СВОЙСТВА ФУНКЦИЙ ПО ЗАДАННЫМ ГРАФИКАМ
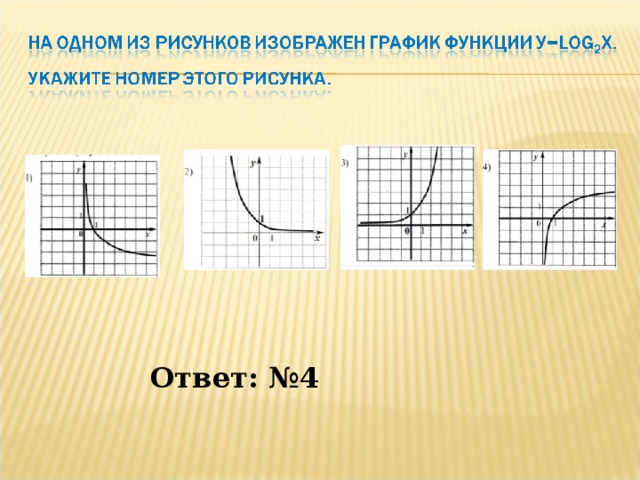
- НА ОДНОМ ИЗ РИСУНКОВ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ У=LOG2Х. УКАЖИТЕ НОМЕР ЭТОГО РИСУНКА. (4)
- НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ У= LOG2(5 – 3X)
3-й этап «Логарифмическая комедия 2>3» :
Сравним: ( 14) и (18) :
( 14) > (18) ; ( )² > ()? тоже не внушающее сомнение.
Большему числу соответствует больший логарифм, значит
lg ( )² > lg ()? 2lg ( ) > 3 lg ()
После сокращения на lg () имеем 2 > 3 . Где ошибка?
4-й «Логарифмические диковинки»
- Вычислить:
А) LOGх у LOGу х
Решение у доски учителем.:
- у х = 1/ LOGх у , х>0, у >0, х≠0, у≠0
- х у LOGу х = LOGх у * (1/ LOGх у) - 1
2. ( Любое число – тремя «2»)
-Любое положительное число можно представить с помощью трёх двоек и математических символов. Например :
Разберём как это получилось:
- Запишем в общем виде «Любое число - тремя двойками»:
- «Расскажи мне, и я забуду, покажи мне, и я запомню. Дай мне сделать самому, и я пойму». О. Хайям.
Самостоятельно:
Проверка.
5-й «Видит око, да ум ещё дальше» (задания записаны на доске)
- Вычислить LOG216 27 + LOG36 16+ LOG6 3
- Решить уравнения:
3.Решить систему уравнения:
4. Указать все натуральные решения неравенства:
6-й «На приз Непера» ( самостоятельная работа)
Учебное пособие - Стр.285 № 977, 988
7-й Подведение итогов урока: -что повторили на уроке?
- выставление оценок
- задание на дом: Учебное пособие «Математика. Подготовка к ЕГЭ-2012» стр.290 №1056, 1060













 3»" width="640"
3»" width="640"
























