Презентация "Геометрический смысл производной. Решение задач из ЕГЭ". В презентации осуществлена подборка задач по теме "Геометрический смысл производной". К каждой задаче приводится решение с чертежами и пояснениями. Для удобства использования, решения задач сразу на слайды не выводятся, а появляются только после нажатия на кнопку "Показать решение". Управление презентацией реализовано с помощью гиперссылок и триггеров. Презентация может быть использована учителями математики при проведении уроков по соответствующей теме и при подготовке к ЕГЭ, а также учащимися для самоподготовки и самоконтроля.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
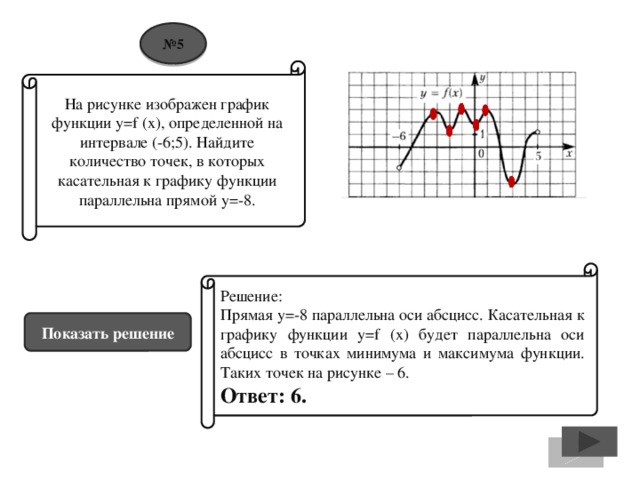
Геометрический смысл производной. Решение задач из ЕГЭ
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Геометрический смысл производной. Решение задач из ЕГЭ»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1540 руб.
2560 руб.
1900 руб.
3170 руб.
1720 руб.
2860 руб.
1690 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

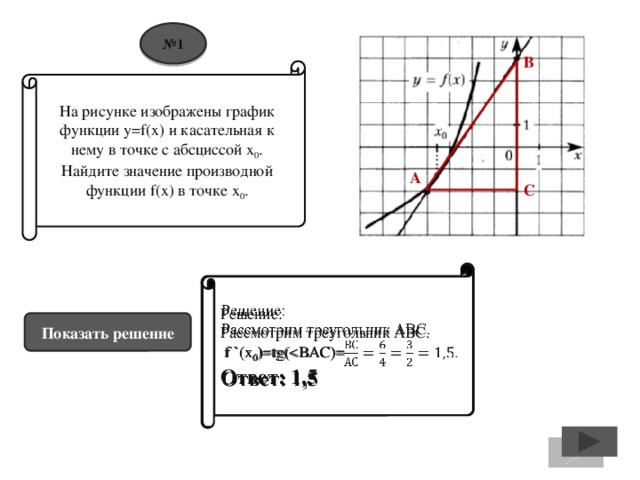
![№ 8 На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-8;5). В какой точке отрезка [-3;2] f(x) принимает наибольшее значение? Решение: На отрезке [-3;2] производная принимает только отрицательные значения. Значит, на этом отрезке функция f(x) – убывает. Следовательно, на левом конце отрезка (в точке -3) значение функции – наибольшее, а на правом конце отрезка (в точке 2) значение функции – наименьшее. Ответ: -3. Показать решение](https://fsd.kopilkaurokov.ru/up/html/2016/12/11/k_584d178d2c4dd/img_user_file_584d178d2c764_8.jpg)
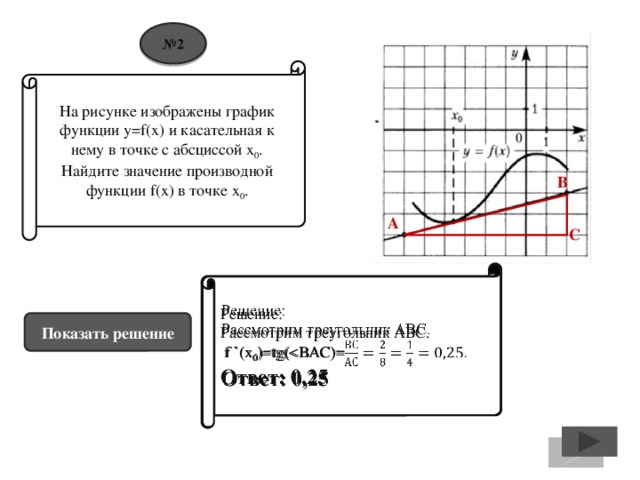
![№ 9 На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-2;9). В какой точке отрезка [1;5] f(x) принимает наименьшее значение? Решение: На отрезке [1;5] производная принимает только положительные значения. Значит, на этом отрезке функция f(x) – возрастает. Следовательно, на левом конце отрезка (в точке 1) значение функции – наименьшее, а на правом конце отрезка (в точке 5) значение функции – наибольшее. Ответ: 1. Показать решение](https://fsd.kopilkaurokov.ru/up/html/2016/12/11/k_584d178d2c4dd/img_user_file_584d178d2c764_9.jpg)
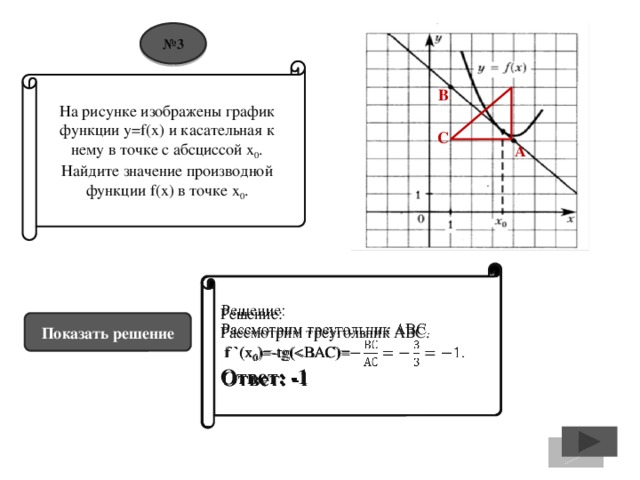
![№ 10 На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-2;18). Найдите количество точек минимума функции f(x) на отрезке [0;15]. Решение: В точках экстремума функции (минимума и максимума) производная равна нулю. Следовательно, нужно найти точки пересечения графика производной с осью абсцисс. Таких точек (попадающих на отрезок [0;15]) на рисунке – 3. В точке минимума производная меняет знак с «-» на «+». На рисунке это выполняется для двух точек. Ответ: 2. Показать решение](https://fsd.kopilkaurokov.ru/up/html/2016/12/11/k_584d178d2c4dd/img_user_file_584d178d2c764_10.jpg)
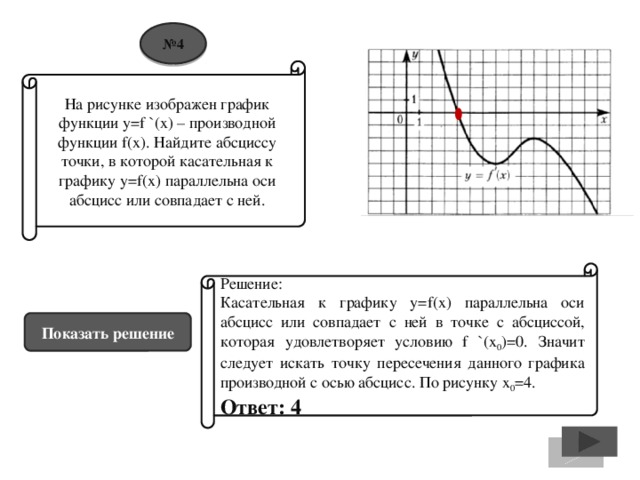
![№ 11 На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-3;11). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. Решение: На промежутке убывания функции f(x), ее производная отрицательна. На рисунке есть два промежутка, на которых производная функции принимает отрицательные значения. Это отрезки [-2;2] и [6;10] . Длина первого отрезка=2-(-2)=4. Длина второго отрезка=10-6=4. Длины обоих отрезков одинаковы. Ответ: 4. Показать решение](https://fsd.kopilkaurokov.ru/up/html/2016/12/11/k_584d178d2c4dd/img_user_file_584d178d2c764_11.jpg)
![№ 12 На рисунке изображен график y=f `(x) – производной функции f(x), определенной на интервале (-2;11). Найдите точку экстремума функции f(x) на отрезке [0;5]. Решение: В точках экстремума функции (минимума и максимума) производная равна нулю. Следовательно, нужно найти точки пересечения графика производной с осью абсцисс. Такая точка (при этом принадлежащая отрезку [0;5]) на рисунке только одна. Это точка х= 3. Ответ: 3. Показать решение](https://fsd.kopilkaurokov.ru/up/html/2016/12/11/k_584d178d2c4dd/img_user_file_584d178d2c764_12.jpg)
















